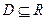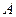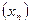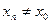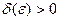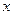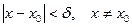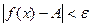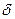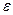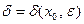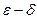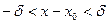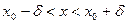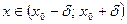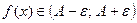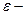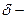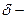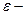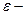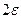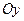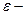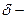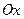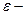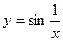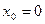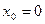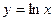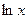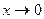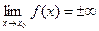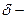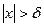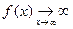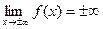Как доказать что функция не имеет предела в точке
Предел функции
Понятие предела.
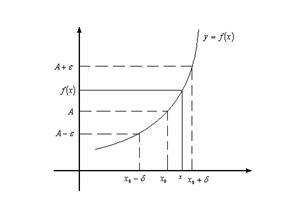
Важную роль в курсе математического анализа играет понятие предела, связанное с поведением функции в окрестности данной точки. Напомним, что \(\delta\) — окрестностью точки \(a\) называется интервал длины \(2\delta\) с центром в точке \(a\), то есть множество Исследуем функцию \(f(x)=\displaystyle \frac \(\triangle\) Функция \(f\) определена при всех \(x\in\mathbb Из этого рисунка видно, что значения функции близки к 2, если значения \(x\) близки к 1 (\(x\neq 1)\). Придадим этому утверждению точный смысл. Пусть задано любое число \(\varepsilon>0\) и требуется найти число \(\delta>0\) такое, что для всех \(x\) из проколотой \(\delta\)-окрестности точки \(x=1\) значения функции \(f(x)\) отличаются от числа 2 по абсолютной величине меньше, чем на \(\varepsilon\). Иначе говоря, нужно найти число \(\delta>0\) такое, чтобы для всех \(x\in\dot_<\delta>(a)\) соответствующие точки графика функции \(y=f(x)\) лежали в горизонтальной полосе, ограниченной прямыми \(y=2-\varepsilon\) и \(y=2+\varepsilon\) (см. рис. 10.1), то есть чтобы выполнялось условие \(f(x)\in U_<\varepsilon>(2)\). В данном примере можно взять \(\delta=\varepsilon\). В этом случае говорят, что функция \(f(x)\) стремится к двум при \(x\), стремящемся к единице, а число 2 называют пределом функции \(f(x)\) при \(x\rightarrow 1\) и пишут \(\displaystyle \lim \(\triangle\) Из графика этой функции (рис. 10.2) видно, что для любого \(\varepsilon>0\) можно найти \(\delta>0\) такое, что для всех \(x\in\dot_<\delta>(0)\) выполняется условие \(f(x)\in U_<\varepsilon>(1)\). В самом деле, прямые \(y=1+\varepsilon\) и \(y=1-\varepsilon\) пересекают график функции \(y=f(x)\) в точках, абсциссы которых равны \(x_<1>=-\varepsilon,\ x_2=\sqrt<\varepsilon>\). Пусть \(\delta\) — наименьшее из чисел \(|x_<1>|\) и \(x_2\), т.e. \(\displaystyle \delta=\min(\varepsilon,\sqrt<\varepsilon>)\). Тогда если \(|x| Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой окрестности точки \(a\), за исключением, быть может, самой точки \(a\), и для каждого \(\varepsilon>0\) найдется число \(\delta>0\) такое, что для всех \(x\), удовлетворяющих условию \(|x-a| 0\ \exists\delta>0:\ \forall x:0 0\ \exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)\in U_<\varepsilon>(A).\nonumber Таким образом, число \(A\) есть предел функции \(f(x)\) в точке \(a\), если для любой \(\varepsilon\)-окрестности числа \(A\) можно найти такую проколотую \(\delta\)-окрестность точки \(a\), что для всех \(x\), принадлежащих этой \(\delta\)-окрестности, соответствующие значения функции содержатся в \(\varepsilon\)-окрестности числа \(A\). В определении предела функции в точке \(a\) предполагается, что \(x\neq a\). Это требование связано с тем, что точка \(a\) может не принадлежать области определения функции. Отсутствие этого требования сделало бы невозможным использование предела для определения производной, так как производная функции \(f(x)\) в точке \(a\) — это предел функции Отметим еще, что число \(\delta\), фигурирующее в определении предела, зависит, вообще говоря, от \(\varepsilon\), то есть \(\delta=\delta(\varepsilon)\). Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой проколотой окрестности точки \(\alpha\), то есть \(\exists\delta_<0>>0:\ \dot_<\delta_<0>>(a)\subset D(f)\), и для любой последовательности \(\ Пользуясь определением предела по Гейне, доказать, что функция $$ \(\triangle\) Достаточно показать, что существуют последовательности \(\ Тогда \(\displaystyle \lim_ Если функция \(f\) определена в проколотой \(\delta_<0>\)-окрестности точки \(a\) и существуют число \(A\) и последовательность \(\ Так, например, для функции \(f(х)=\displaystyle \sin\frac<1> Определения предела функции по Коши и по Гейне эквиваленты. \(\circ\) В определениях предела функции \(f(x)\) по Коши и по Гейне предполагается, что функция \(f\) определена в некоторой проколотой окрестности точки \(a\), то есть существует число \(\delta_0>0\) такое, что \(\dot_<\delta_<0>>\in D(f)\). Пусть \(а\) — предельная точка числового множества \(E\), то есть такая точка, в любой окрестности которой содержится по крайней мере одна точка множества \(E\), отличная от \(a\). Тогда число \(A\) называют пределом по Коши функции \(f(x)\) в точке \(a\) по множеству \(E\) и обозначают \(\displaystyle \lim_ Число \(A\) называют пределом слева функции \(f(x)\) в точке a и обозначают \(\displaystyle \lim_ Отметим еще, что если Аналогично Аналогичный смысл имеют записи вида Например, Говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке бесконечный предел, и пишут \(\lim_ В этом случае функцию \(f(x)\) называют бесконечно большой при \(x\rightarrow a\). Например, если \(f(x)=1/x\), то \(\displaystyle \lim_ Аналогично говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке предел, равный \(+\infty\), и пишут \(\displaystyle \lim_ Если $$ то говорят, что число \(A\) есть предел функции \(f(x)\) при x, стремящемся к плюс бесконечности, и пишут \(\displaystyle \lim_ Например, если \(f(x)=\displaystyle\frac<3-2x> Если \(\forall\varepsilon>0 \ \exists\delta>0:\forall x\in U_<\delta>(-\infty)\rightarrow f(x)\in U_<\varepsilon>(A)\), то есть неравенство \(|f(x)-A| 0\ \exists\delta>0:\forall x\in U_<\delta>(\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber Точно так же вводится понятие бесконечного предела в бесконечности. Например,запись \(\displaystyle \lim_ Покажем, что функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, то есть свойствами, которые справедливы в окрестности этой точки. Если функция \(f(x)\) имеет предел в точке \(a\), то существует такая проколотая окрестность точки \(a\), в которой эта функция ограничена. \(\circ\) Пусть \(\displaystyle \lim_ Свойство сохранения знака предела. Если \(\displaystyle \lim_ \(\circ\) Согласно определению предела по заданному числу \(\varepsilon = \frac<|A|><2>>0\) можно найти такое число \(\delta>0\), что для всех \(x\in\dot_<\delta>(a)\) выполняется неравенство \(\displaystyle |f(x)-A| 0\), то из левого неравенства \eqref Если \(\displaystyle \lim_ \(\circ\) В силу определения предела по заданному числу \(\varepsilon=\frac<|B|><2>\) можно найти число \(\delta>0\), такое, что для всех \(x\in\dot_\delta(a)\) выполняется неравенство Если существует число \(\delta>0\) такое, что для всех \(\dot_<\delta>(a)\) выполняются неравенства \(\circ\) Воспользуемся определением предела функции по Гейне. Пусть \(\ Так как, согласно условию \eqref \(\circ\) Для доказательства этого свойства достаточно воспользоваться определением предела функции по Гейне и соответствующими свойствами пределов последовательностей. \(\bullet\) Бесконечно малые функции обладают следующими свойствами: Эти свойства легко доказать, используя определения бесконечно малой и ограниченной функции, либо с помощью определения предела функции по Гейне и свойств бесконечно малых последовательностей. Из свойства 2) следует, что произведение конечного числа бесконечно малых при \(x\rightarrow a\) функций есть бесконечно малая при \(x\rightarrow a\) функция. Из определения предела функции и определения бесконечно малой функции следует, что число \(A\) является пределом функции \(f(x)\) в точке \(a\) тогда и только тогда, когда эта функция представляется в виде Если функции \(f(x)\) и \(g(x)\) имеют конечные пределы в точке \(а\), причем \(\displaystyle \lim_ \(\circ\) Для доказательства этих свойств достаточно воспользоваться определением предела функции по Гейне и свойствами пределов последовательностей. \(\bullet\) Отметим частный случай утверждения \eqref Ранее мы уже ввели понятие монотонной функции. Докажем теорему о существовании односторонних пределов у монотонной функции. Если функция \(f\) определена и является монотонной на отрезке \([a,b]\), то в каждой точке \(x_<0>\in(a,b)\) эта функция имеет конечные пределы слева и справа, a в точках \(а\) и \(b\) — соответственно правый и левый пределы. \(\circ\) Пусть, например, функция \(f\) является возрастающей на отрезке \([a,b]\). Зафиксируем точку \(х_0\in\)(а, \(b\)]. Тогда В силу условия \eqref Если функция \(f\) определена и возрастает на отрезке \([a,b],\ x_<0>\in(a,b),\) то Теорема о пределе монотонной функции справедлива для любого конечного или бесконечного промежутка. При этом, если \(f\) — возрастающая функция, не ограниченная сверху на \((a,b)\), то \(\displaystyle \lim_ Будем говорить, что функция \(f(x)\) удовлетворяет в точке \(x=a\) условию Коши, если она определена в некоторой проколотой окрестности точки \(a\) и Пусть существует число \(\delta >0\) такое, что функция \(f(x)\) определена в проколотой \(\delta\) — окрестности точки \(a\), и пусть для каждой последовательности <\(x_n\)>, удовлетворяющей условию \(x_n\in\dot_<\delta>(a)\) при всех \(n\in\mathbb \(\circ\) Образуем последовательность Для того чтобы существовал конечный предел функции \(f(x)\) в точке \(x = a\) необходимо и достаточно, чтобы эта функция удовлетворяла в точке a условию Коши \eqref \(\circ\) Необходимость. Пусть \(\displaystyle \lim_ Теорема 3 остается в силе, если точку \(a\) заменить одним из символов \(a-0, a+0,-\infty, +\infty\); при этом условие \eqref Тема 1. Предел функции Раздел: Предел и непрерывность функции Допустим, что функция Можно дать определение функции в точке по Гейне (см. конспект1-го курса) и по Коши. Определение 1 (по Гейне). Число Определение 2 (по Коши).Число А называется пределом функции Заметим, что число Первое определение называется также определением предела функции «на языке последовательностей», а второе – определением предела «на языке Определение 2 можно дать в геометрической форме. Используя свойство модуля неравенство (1) можно записать в виде Аналогично из (2) Определение 3 (геометрическая форма определения Коши). Число А – предел функции Дадим графическую иллюстрацию этого определения. Для того, чтобы доказать графически, что число А является пределом функции в точке Можно доказать эквивалентность определений предела по Коши и по Гейне. Не всякая функция имеет предел в точке. Например, функция Т.о. относительно предела функции в точке возможны следующие случаи: I.Функция имеет предел в точке. Это число. II. Функция не имеет предела в точке: 1)она является бесконечно большой в этой точке, и хотя предела в этом случае нет, записывают 2)Предел не определен вообще и не ясно, к чему стремится функция в данной точке. Кроме определения предела в точке рассматривают предел функции на бесконечности, т.е. при I. Предел существует, и это число (рис. 1); II. Предел не существует: 1) 2) предел неопределен вообще (рис. 3).
$$
U_<\delta>(a)=\Рис. 10.1
Два определения предела функции и их эквивалентность.
Определение предела по Коши.
$$
$$
F(x) = \frac
$$
которая не определена в точке \(a\).Определение предела по Гейне.
f(x)=\sin\frac<1>
$$
не имеет предела в точке \(x=0\).Рис. 10.3
Эквивалентность двух определений предела.
$$
\forall\varepsilon>0\quad \exists\delta>0:\quad\forall x\in \dot_<\delta>(a)\cap E\rightarrow|f(x)-A|Различные типы пределов.
Односторонние конечные пределы.
$$
\forall\varepsilon>0\quad\exists\delta>0:\quad\forall x\in(a-\delta,a)\rightarrow|f(x)-A_<1>| 0\quad\exists\delta>0:\ \forall x\in (a,a+\delta)\rightarrow|f(x)-A_2| 0,
\end
$$
график которой изображен на рис. 10.4 \(\displaystyle \lim_Рис. 10.4
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x)\in[A,A+\varepsilon),
$$
то есть значения функции лежат в правой \(\varepsilon\)-полуокрестности числа \(A\), то пишут \(\displaystyle \lim_
$$
\displaystyle \<\lim_
$$
Например, для функции
$$
\varphi (x)=\left\<\begin
1-x,\ если\ x 0,
\end
$$
график которой изображен на рис. 10.5, \(\displaystyle \lim_Рис. 10.5
$$
\lim_
$$
$$
\displaystyle \<\lim_
$$Бесконечные пределы в конечной точке.
$$
\forall\varepsilon>0\quad\exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow|f(x)|>\varepsilon.\label
$$Рис. 10.6
$$
\forall\varepsilon>0\quad\exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x) Рис. 10.7
Рис. 10.8
Предел в бесконечности.
\forall\varepsilon>0\exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber
$$
$$
то говорят, что число A есть предел функции f(x) при x, стремящемся к бесконечности, и пишут \(\displaystyle \lim_
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(-\infty).\nonumber
$$
Аналогично определяются бесконечные пределы при \(x\rightarrow\infty\) и \(x\rightarrow-\infty.\)Свойства пределов функций.
Локальные свойства функции, имеющей предел.
$$
f(x)>\frac<2>>0\ для\ x\in\dot_<\delta>(a).\nonumber
$$
Если \(A Свойство 3
$$
|g(x)-B| \frac<|B|><2>\),и поэтому \(\displaystyle \frac<1> <|g(x)|>Свойство 1
$$
g(x)\leq f(x)\leq h(x),\label
$$
и если
$$
\lim_
$$
то существует \(\displaystyle \lim_
$$
g(x_
$$
то в силу свойств пределов последовательностей \(\displaystyle \lim_
$$
f(x)=A+a(x),\nonumber
$$ где \(a(x)\) — бесконечно малая при \(x\rightarrow a\) функция.Свойства пределов, связанные с арифметическими операциями.
$$
\lim_
$$
то есть постоянный множитель можно вынести за знак предела.Пределы монотонных функций.
$$
\forall x\in[a,x_<0>)\rightarrow f(x)\leq f(x_<0>).\label
$$
$$
\sup_
$$
Согласно определению предела слева это означает, что существует
$$
\lim_
$$
Итак,
$$
f(x_<0>-0)=\sup_
$$
f(x_<0>-0) Замечание.Критерий Коши существования предела функции.
$$
\forall\varepsilon>0\quad \exists\delta=\delta(\varepsilon)>0:\ \forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)|
$$
\lim_
$$
и
$$
\lim_
$$
где \(\widetilde
$$
x_<1>,\widetilde
$$
и обозначим k-й член этой последовательности через \(y_
$$
\forall\varepsilon>0 \ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow|f(x)-A| 0\) можно найти число \(\delta=\delta_\varepsilon>0\) такое, что
$$
\forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)| 0,\) указанное в условии \eqref
$$
\forall n>N_<\varepsilon>\rightarrow 0 Замечание.Предел функции в точке и на бесконечности