Как доказать что функция общего вида
Четные и нечетные функции
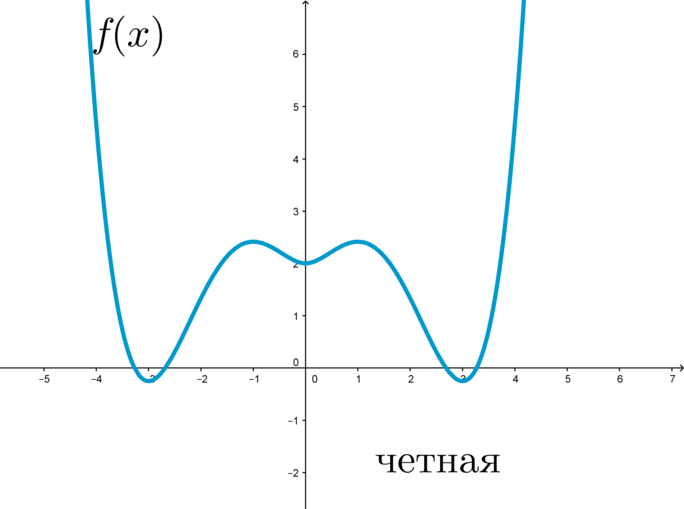
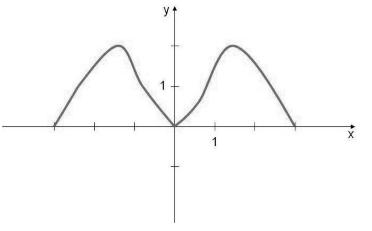
График четной функции симметричен относительно оси \(y\) :
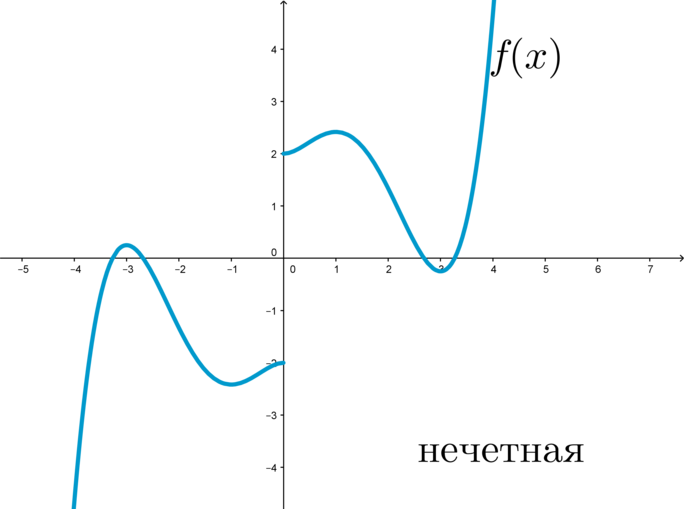
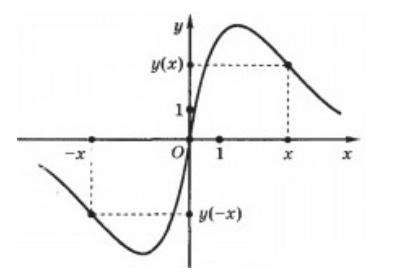
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
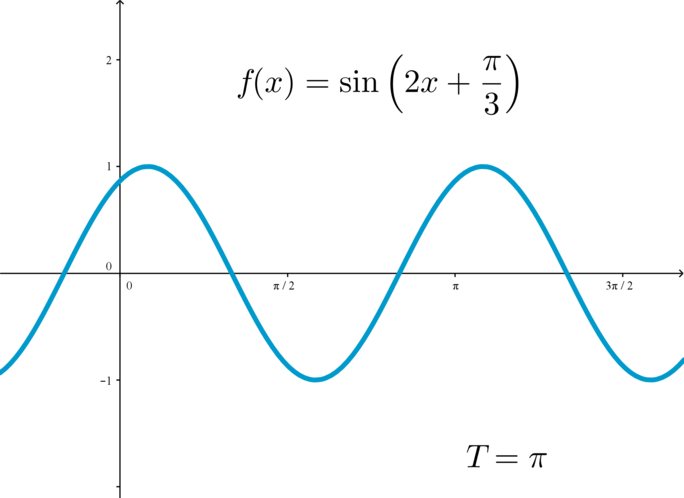
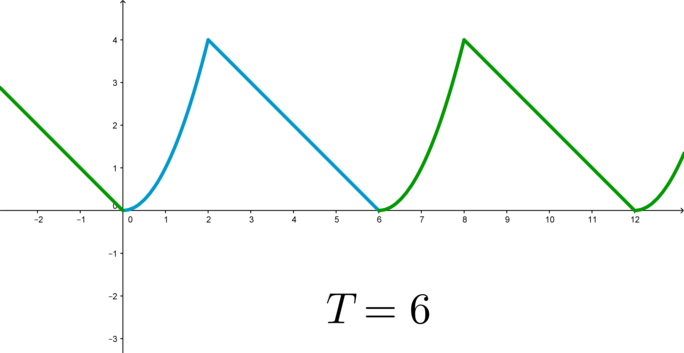
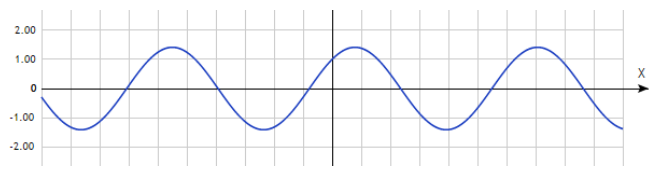
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Когда функция является функцией общего вида?
Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида.
Как понять что функция общего вида?
Какие функции четные нечетные или общего вида?
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат). Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
Какая из функций будет четной?
Если график функции y=f(x) симметричен относительно оси ординат, то y=f(x) — чётная функция. Если график функции y=f(x) симметричен относительно начала координат, то y=f(x) — нечётная функция.
Как определить четная или нечетная функция 11 класс?
Периодичность. Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x). Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Что является функцией?
Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Что значит косинус четная функция?
косинус – четная функция, f(–x) = f(x). Значит, можно исследовать свойства функции y = cos х на отрезке [0, p], а затем учесть ее четность и периодичность. При х = 0 точка А лежит на оси Ох, ее абсцисса равна 1, а потому cos 0 = 1.
Как исследовать функцию на четность и нечетность?
Чтобы исследовать функцию на четность и нечетность, надо проверить, симметрична ли область определения функции относительно начала координат, то есть выполняется ли равенство − = ( ), и если это так, значит, функция четная. Если выполняется равенство − = − ( ), значит, функция нечетная.
Какая из функций является показательной?
Определение: Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Какая сейчас неделя четная или нет?
Расписание четности недель
| 01.09 – 06.09 — нечетная | 01.02 – 07.02 — нечетная |
|---|---|
| 07.09 – 12.09 — четная | 08.02 – 14.02 — четная |
| 14.09 – 20.09 — нечетная | 15.02 – 21.02 — нечетная |
| 21.09 – 27.09 — четная | 22.02 – 28.02 — четная |
| 28.09 – 04.10 — нечетная | 29.02 – 06.03 — нечетная |
Какие есть свойства функции?
Основные свойства функций.
Какие тригонометрические функции четные какие нечетные?
Тригонометрические функции бывают четными и нечетными.
Как понять четная или нечетная функция 10 класс?
Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) – чётная функция. Если график функции у = f(х) симметричен относительно начала координат, то у = f(х) – нечётная функция.
Как определить является ли функция периодической?
Функция
1. Понятие функции
2. Cвойства функций
2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1 ) x2, f(x1) ) f(x2).
область определения (-∞,∞)
область значений (0; ∞)
общего вида
возрастает на (-∞,∞), если a>1;
убывает на (-∞,∞), если 0 непериодическая
Логарифмическая функция
у = log ₐ x (a>0 a≠1)
область определения (0,∞)
область значений (-∞; ∞)
общего вида
возрастает на (0,∞), если a>1;
убывает на (0,∞), 0 непериодическая
Тригонометрические функции
y = sin x
область определения (-∞; ∞)
область значений [-1; 1]
нечетная
возрастает на [-π/2 + 2πn, π/2 + 2πn];
убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ;
период Т=2π
y = cos x
область определения (-∞; ∞)
область значений [-1; 1]
четная
возрастает на [-π + 2πn, 2πn];
убывает на [2πn, π + 2πn], nϵZ;
период Т=2π
y = tg x
область определения
(-π/2 + πn, π/2 + πn) nϵZ;
область значений (-∞; ∞)
нечетная
возрастает на (-π/2 + πn, π/2 + πn) nϵZ;
период Т=π
y = ctg x
область определения
(πn, π + πn) nϵZ;
область значений (-∞; ∞)
нечетная
убывает на (πn, π + πn) nϵZ;
период Т=π
y = arcsin x
область определения [-1; 1]
область значений [-π/2; π/2]
нечетная
возрастает на [-1; 1]
y = arccos x
область определения [-1; 1]
область значений [0; π]
функция центрально-симметрична относительно точки (0; π/2)
убывает на [-1; 1]
y = arctg x
область определения (-∞; ∞)
область значений [-π/2; π/2]
нечетная
возрастает на (-∞; ∞)
y = arcctg x
область определения (-∞; ∞)
область значений [0; π]
ни четная, ни нечетная
убывает на (-∞; ∞)
Как доказать что функция общего вида. Как определять четные и нечетные функции
Назад Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Оборудование: мультимедийная установка, интерактивная доска, раздаточный материал.
Формы работы: фронтальная и групповая с элементами поисково-исследовательской деятельности.
Информационные источники:
1.Алгебра9класс А.Г Мордкович. Учебник.
2.Алгебра 9класс А.Г Мордкович. Задачник.
3.Алгебра 9 класс. Задания для обучения и развития учащихся. Беленкова Е.Ю. Лебединцева Е.А
1. Организационный момент
Постановка целей и задач урока.
2. Проверка домашнего задания
№10.17 (Задачник 9кл. А.Г. Мордкович).
а) у = f (х ), f (х ) =
0,4
4. f (х ) >0 при х > 0,4 ; f (х ) –1
– Выполняя данную работу, ребята мы выявили ещё одно свойство функции, незнакомое вам, но не менее важное, чем остальные – это чётность и нечетность функции. Запишите тему урока: «Чётные и нечётные функции», наша задача – научиться определять чётность и нечётность функции, выяснить значимость этого свойства в исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем (стр. 110). Слайд
Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд
Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.
– У чётных функций область определения – симметричное множество? У нечётных?
– Если же D(f ) – несимметричное множество, то функция какая?
– Таким образом, если функция у = f (х ) – чётная или нечётная, то её область определения D(f ) – симметричное множество. А верно ли обратное утверждение, если область определения функции симметричное множество, то она чётна, либо нечётна?
– Значит наличие симметричного множества области определения – это необходимое условие, но недостаточное.
– Так как же исследовать функцию на четность? Давайте попробуем составить алгоритм.
Алгоритм исследования функции на чётность
1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.
2. Составить выражение для f (– х ).
1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.
2) h (– х) = (–х) 5 + – х5 –= – (х 5 +),
3) h(– х) = – h (х) => функция h(х) = х 5 + нечётная.
у = f (х ), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.
а) у = х 2 · (2х – х 3), б) у =
Постройте график функции у = f (х ), если у = f (х ) – нечётная функция.
Взаимопроверка по слайду.
6. Задание на дом: №11.11, 11.21,11.22;
Доказательство геометрического смысла свойства чётности.
***(Задание варианта ЕГЭ).
1. Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(х ) = х (х + 1)(х + 3)(х – 7). Найдите значение функции h(х ) = при х = 3.
7. Подведение итогов
Основные свойства функций.
В элементарной математике изучаются функции только на множестве действительных чисел.
Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Доказать, что у = х 3
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
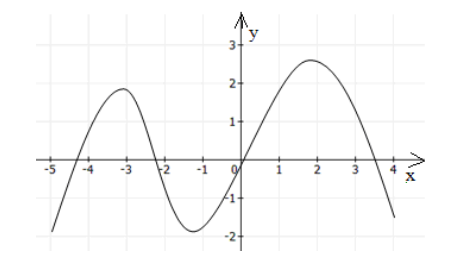
Функция общего вида
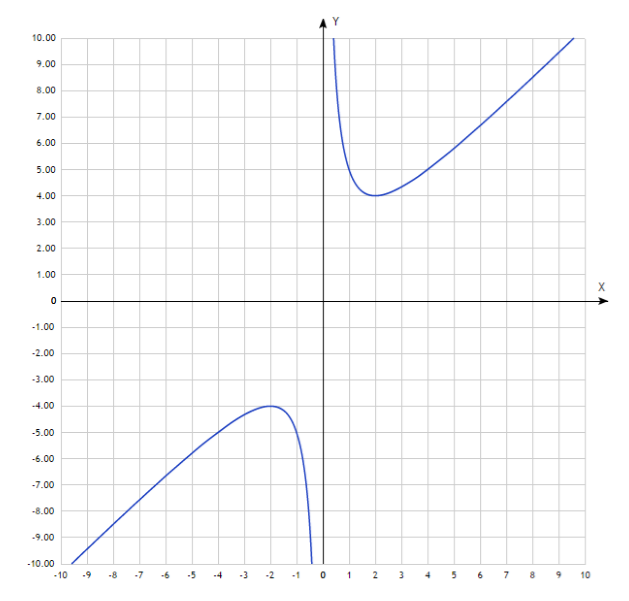
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021