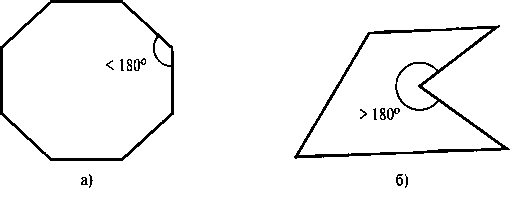Как доказать что многоугольник вогнутый
Как доказать что многоугольник вогнутый
Термином вырожденный многоугольник часто описывают набор вершин, которые являются коллинеарными или координаты которых повторяются. Коллинеарные вершины дают прямолинейный отрезок. Вершины с повторяющимися координатами могут дать многоугольную фигуру с лишними линиями, перекрывающимися сторонами или сторонами, длина которых равна 0. Иногда термин вырожденный многоугольник еще применяется к списку вершин, который состоит из менее, чем трех точек.
Устойчивые графические пакеты могут не воспринимать вырожденные или неплоские наборы вершин. Однако их распознавание требует дополнительной обработки, поэтому в графических системах выбор ограничивающих условий, как правило, оставляется на усмотрение программиста.
Вогнутые многоугольники также создают дополнительные проблемы. Реализация алгоритмов закрашивания и других графических процедур для вогнутых многоугольников намного сложнее, поэтому, как правило, перед обработкой эффективнее разделить вогнутый многоугольник на набор выпуклых. Как и другие алгоритмы предварительной обработки многоугольников, функции разделения вогнутого многоугольника часто не входят в графическую библиотеку. Для некоторых пакетов, в том числе и OpenGL, необходимо, чтобы все закрашиваемые многоугольники были выпуклыми. Кроме того, в некоторых системах допускается только закрашивание треугольных областей, что значительно упрощает многие алгоритмы создания изображений.
РАСПОЗНАВАНИЕ ВОГНУТЫХ МНОГОУГОЛЬНИКОВ
У вогнутого многоугольника по крайней мере один внутренний угол больше, чем 180°. Кроме того, продолжения некоторых сторон вогнутого многоугольника будут пересекать другие ребра, а некоторые пары внутренних точек дадут отрезки, пересекающие границы многоугольника. Следовательно, любой из этих признаков вогнутого многоугольника можно положить в основу алгоритма распознавания вогнутых многоугольников.
Значение многоугольника
Содержание:
Что такое многоугольник:
Многоугольник это геометрическая фигура в закрытом виде, имеющем более 3-х сторон, углов и вершин. Слово многоугольник происходит от греческого полицейский Что это значит «Много» Y гоно Что это значит «стороны «.
Многоугольники именуются в соответствии с количеством сторон, которые у них есть, например, четырехугольник с четырьмя сторонами называется четырехугольником, многоугольник с восемью сторонами называется восьмиугольником и так далее.
Точно так же многоугольник вызывается ограниченная территория который представляет собой городскую единицу для городских, промышленных, военных целей, среди прочего. Когда упоминается термин «промышленная зона», это означает, что предприятия различных компаний расположены в городской зоне города.
Правильный и неправильный многоугольник
Правильный многоугольник Его стороны имеют одинаковую длину, его внутренние углы имеют одинаковую меру, а его вершины описываются по окружности, это равносторонние многоугольники, так как их стороны имеют одинаковую длину и равные углы, потому что углы имеют одинаковые размеры. Тем не мение, неправильный многоугольник он противоположен правильному многоугольнику, поскольку его стороны не равны по длине, его внутренние углы не равны среднему значению, а его вершины не описываются в круге.
Выпуклый и вогнутый многоугольник
Вписанный и описанный многоугольник
Вписанный многоугольник это означает, что геометрическая фигура находится внутри другой геометрической фигуры, то есть все стороны многоугольника заключены в рамки другой фигуры. Описанный многоугольник Это противоположно предыдущему, поскольку многоугольник внутри содержит другую геометрическую фигуру.
Полигон частот
Уиллис многоугольник
Многоугольник уиллиса Это анатомическая структура, в которой несколько артерий остаются объединенными в нижней части мозга с функцией, заключающейся в том, что внутренние сонные артерии переходят в более мелкие артерии для распределения кровотока во всех областях мозга. Его называют многоугольником Уиллиса, поскольку он имеет форму семиугольника.
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
    |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
 |
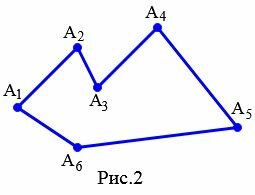На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
  |
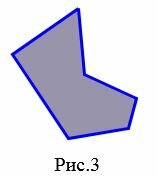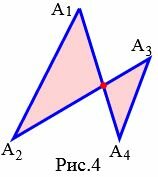На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
 |
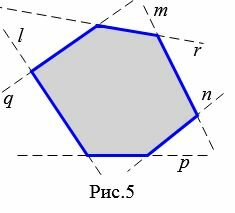На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
 |
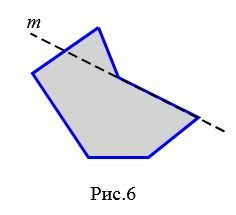На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
  |
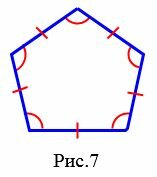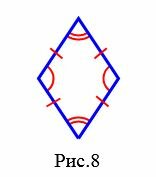На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
 |
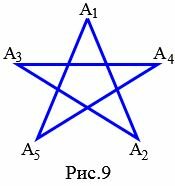На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
 |
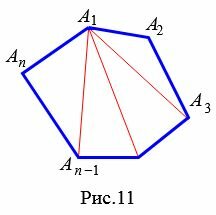Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Разница между вогнутыми и выпуклыми полигонами
Ключевая разница: Многоугольник, у которого все внутренние углы меньше 180 градусов, известен как выпуклый многоугольник. С другой стороны, многоугольник с одним или несколькими внутренними углами, пр
Содержание:
Многоугольник с любым из внутренних углов больше 180 градусов называется вогнутым многоугольником. Другими словами, существует вогнутый многоугольник с внутренним углом отражения. Простой тест линии может использоваться, чтобы отличить вогнутый многоугольник с выпуклым многоугольником. Если рисуется линия, проходящая через многоугольник, и она всегда проходит только через две линии или многоугольники, составляющие форму, то в этом случае форма многоугольника является выпуклой. С другой стороны, если тот же процесс повторяется в вогнутой форме, линия может проходить через более чем две линии. В трехмерных формах можно провести один и тот же тест, чтобы различить их.
Важно отметить, что все диагонали выпуклого многоугольника полностью лежат внутри многоугольника. Однако в вогнутом многоугольнике некоторые диагонали всегда будут лежать вне многоугольника. Все правильные многоугольники являются выпуклыми (многоугольник, у которого все стороны равны и все внутренние углы равны). Выпуклые многоугольники легче рисовать по сравнению с вогнутыми многоугольниками.
Сравнение выпуклых и вогнутых полигонов:
Вогнутый многоугольник
Выпуклый многоугольник
Многоугольник с одним или несколькими внутренними углами, превышающими 180 градусов, называется вогнутым многоугольником.
Многоугольник, у которого все внутренние углы меньше 180 градусов, известен как выпуклый многоугольник.
Вмятина (кривая внутрь)
Все его линии кривые снаружи
Линия содержит сторону многоугольника, содержащую точку внутри многоугольника.
Ни одна линия, содержащая сторону многоугольника, не содержит точки внутри многоугольника.
Перекрестное произведение смежных векторных пар составляет Разница Между