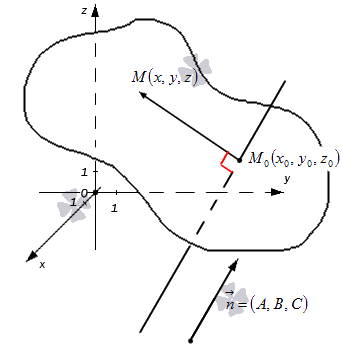
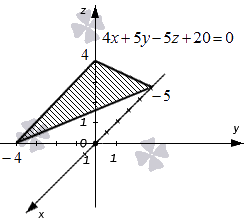
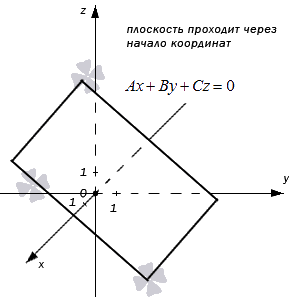
Как доказать что плоскость проходит через точку
Как доказать что плоскость проходит через точку
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 6 : 1, на ребре BB1 — точка F так, что B1F : FB = 3 : 4, а точка T — середина ребра B1C1. Известно, что AD = 30, AA1 = 35.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Значит, треугольники D1A1E и TB1F подобны, причём прямые D1A1 и B1C1 параллельны, прямые A1E и B1F тоже параллельны. Поэтому прямые ED1 и FT также параллельны. Если плоскость EFT не проходит через точку D1, то получается, что в плоскости AA1D1D через точку E проходят две различные прямые, параллельные прямой FT. Получили противоречие.
б) Сечение параллелепипеда плоскостью EFT — трапеция. Проведём через точку F прямую, параллельную прямой AB. Получим точку P на ребре AA1.
Следовательно, EF = D1T, и трапеция EFTD1 равнобедренная. Проведём в ней высоту TH.
Тогда площадь трапеции равна
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Как доказать что плоскость проходит через точкуНа ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 6 : 1, на ребре BB1 — точка F так, что B1F : FB = 3 : 4, а точка T — середина ребра B1C1. Известно, что а) Докажите, что плоскость EFT проходит через вершину D1. б) Найдите площадь сечения параллелепипеда плоскостью EFT. Значит, треугольники D1A1E и TB1F подобны, причём прямые D1A1 и B1C1 параллельны, прямые A1E и B1F тоже параллельны. Поэтому прямые ED1 и FT также параллельны. Если плоскость EFT не проходит через точку D1, то получается, что в плоскости AA1D1D через точку E проходят две различные прямые, параллельные прямой FT. Получили противоречие. б) Сечение параллелепипеда плоскостью EFT — трапеция. Проведём через точку F прямую, параллельную прямой AB. Получим точку P на ребре AA1. Следовательно, EF = D1T, и трапеция EFTD1 равнобедренная. Проведём в ней высоту TH. Продолжим изучение темы уравнение плоскости. В этой статье мы всесторонне рассмотрим общее уравнение плоскости в трехмерном пространстве в фиксированной прямоугольной системе координат. Сначала получим вид общего уравнения плоскости, приведем примеры и необходимые пояснения. Далее остановимся на общем уравнении плоскости, проходящей через заданную точку пространстве. В заключении разберем частные случаи общего уравнения плоскости, рассмотрим общее неполное уравнение плоскости и приведем подробные решения задач. Навигация по странице. Прежде чем записать общее уравнение плоскости, напомним определение прямой перпендикулярной к плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Из этого определения следует, что любой нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в этой плоскости. Этот факт мы используем при доказательстве следующей теоремы, которая задает вид общего уравнения плоскости. Начнем с доказательства первой части теоремы. Равенство Приступим к доказательству второй части. Пусть нам дана плоскость, проходящая через точку Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет Уравнение Общее уравнение плоскости вида Немного поясним смысл теоремы. Приведем пример, иллюстрирующий последнюю фразу. Общее уравнение плоскости, проходящей через точку.Еще раз повторим, что точка Принадлежат ли точки Подставим координаты точки М0 в общее уравнение плоскости: Проделаем такую же процедуру с координатами точки N0 : М0 лежит в плоскости, а N0 – не лежит. Из доказательства теоремы об общем уравнении плоскости виден один полезный факт: вектор Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости Теперь рассмотрим обратную задачу – задачу составления уравнения плоскости, когда известны координаты ее нормального вектора. Очевидно, что существует бесконечно много параллельных плоскостей, нормальным вектором которых является вектор Общее уравнение плоскости с нормальным вектором Это уравнение можно было получить и иначе. Очевидно, что множество точек трехмерного пространства Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку Приведем два решения этой задачи. Из условия имеем Теперь второй вариант решения. Пусть Существует множество аналогичных задач на составление общего уравнения плоскости, в которых сначала требуется найти координаты нормального вектора плоскости. Самые распространенные из них это задачи на нахождение уравнения плоскости, проходящей через точку параллельно заданной плоскости и задачи на составление уравнения плоскости, проходящей через точку перпендикулярно к заданной прямой. Неполное общее уравнение плоскости.Рассмотрим все возможные общие неполные уравнения плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве. Разберем решения нескольких примеров на составление неполного уравнения плоскости. Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку Приведем второй способ решения этой задачи. Общее уравнение плоскости : описание, примеры, решение задачВ статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости. Общее уравнение плоскости: основные сведенияТакже вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости. Теорема состоит из двух частей. Разберем доказательство каждой из них. Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства. Раскроем чуть шире смысл теорем. Укажем пример как иллюстрацию этих утверждений. Общее уравнение плоскости, проходящей через точкуРешение Подставим координаты точки М 0 в исходной уравнение плоскости: Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит. Решение Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора. Возможно получить это уравнение другим способом. Решение Рассмотрим два способа решения. Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда: Неполное общее уравнение плоскостиРазберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства. A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0 Решение Задачу возможно решить еще одним способом. Решение
|
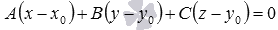 представляет собой необходимое и достаточное условие перпендикулярности векторов
представляет собой необходимое и достаточное условие перпендикулярности векторов  и
и 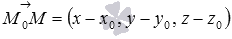 . Иными словами, координаты плавающей точки
. Иными словами, координаты плавающей точки 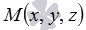 удовлетворяют уравнению
удовлетворяют уравнению 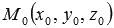 . Другими словами, уравнение
. Другими словами, уравнение  определяет эту же плоскость. Первая часть теоремы доказана.
определяет эту же плоскость. Первая часть теоремы доказана.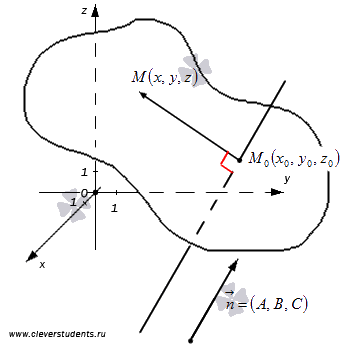
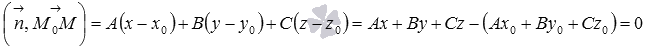 . Приняв
. Приняв 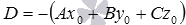 , уравнение примет вид
, уравнение примет вид  , где
, где  — некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координат Oxyz плоскость, совпадающую с плоскостью
— некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координат Oxyz плоскость, совпадающую с плоскостью  и
и  задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
 и
и  плоскости, общее уравнение которой имеет вид
плоскости, общее уравнение которой имеет вид  .
. . В результате приходим к верному равенству, следовательно, точка
. В результате приходим к верному равенству, следовательно, точка  . Получаем неверное равенство, поэтому, точка
. Получаем неверное равенство, поэтому, точка  . Запишите координаты всех нормальных векторов этой плоскости.
. Запишите координаты всех нормальных векторов этой плоскости.
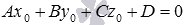 . Вычтем из левой и правой части равенства
. Вычтем из левой и правой части равенства  .
. , а
, а  — нормальный вектор этой плоскости.
— нормальный вектор этой плоскости. . Подставляем эти данные в общее уравнение плоскости, проходящей через точку
. Подставляем эти данные в общее уравнение плоскости, проходящей через точку 
 по координатам точек начала и конца:
по координатам точек начала и конца:  . Для получения требуемого общего уравнения плоскости осталось только воспользоваться необходимым и достаточным условием перпендикулярности векторов
. Для получения требуемого общего уравнения плоскости осталось только воспользоваться необходимым и достаточным условием перпендикулярности векторов  :
: 




 .
.