Как доказать что призма прямая
Призма и ее виды
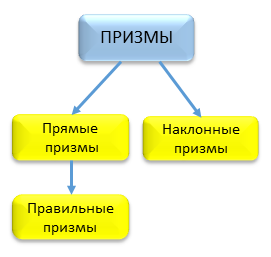
Рассматриваемый класс фигур представлен призмами нескольких видов. Перечислим их кратко:
Каждая фигура относится к одному из перечисленных трех видов классификации. Во время решения геометрических задач проще всего выполнять расчеты для правильных и прямых призм. Последние подробнее рассмотрим в следующих пунктах статьи.
Выше было сказано, что с прямыми фигурами удобно работать при решении задач. Это связано с тем, что высота совпадает с длиной бокового ребра. Последний факт облегчает процесс вычисления объема фигуры и площади ее боковой поверхности.
Объем прямой призмы
То есть произведение высоты на площадь основания даст искомое значение V. Поскольку у прямой призмы основания равны, то для определения площади So можно брать любое из них.
Преимущество использования приведенной выше формулы именно для прямой призмы в сравнении с другими ее видами заключается в том, что высоту фигуры найти очень просто, так как она совпадает с длиной бокового ребра.
Площадь боковой поверхности
Предположим, что в основании призмы лежит произвольный n-угольник, стороны которого равны ai. Индекс i пробегает значения от 1 до n. Площадь одного прямоугольника вычисляется так:
Площадь поверхности боковой Sb нетрудно вычислить, если сложить все площади Si прямоугольников. В таком случае получаем конечную формулу для Sb прямой призмы:
Таким образом, чтобы определить площадь боковой поверхности для прямой призмы, необходимо умножить ее высоту на периметр одного основания.
Задача с треугольной призмой
Для начала вычислим объем прямой призмы. Треугольник (прямоугольный), находящийся в ее основаниях, имеет площадь:
So = a1*a2/2 = 12*8/2 = 48 см2.
Как можно догадаться, a1 и a2 в этом равенстве являются катетами. Зная площадь основания и высоту (см. условие задачи), можно воспользоваться формулой для V:
V = So*h = 48*15 = 720 см3.
Полная площадь фигуры образована двумя частями: площадями оснований и боковой поверхностью. Площади двух оснований равны:
S2o = 2*So = 48*2 = 96 см2.
Для вычисления площади боковой поверхности необходимо знать периметр прямоугольного треугольника. Вычислим по теореме Пифагора его гипотенузу a3, имеем:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 см.
Тогда периметр треугольника основания прямой призмы составит:
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 см.
Применяя формулу для Sb, которая была записана в предыдущем пункте, получаем:
Sb = h*P = 15*34,42 = 516,3 см.
Сложив площади S2o и Sb, мы получим полную площадь поверхности изучаемой геометрической фигуры:
S = S2o + Sb = 96 + 516,3 = 612,3 см2.
Треугольная призма, которую изготавливают из специальных видов стекла, применяется в оптике при изучении спектров излучающих свет объектов. Такие призмы способны разлагать свет на составляющие частоты благодаря явлению дисперсии.
Как доказать что призма прямая
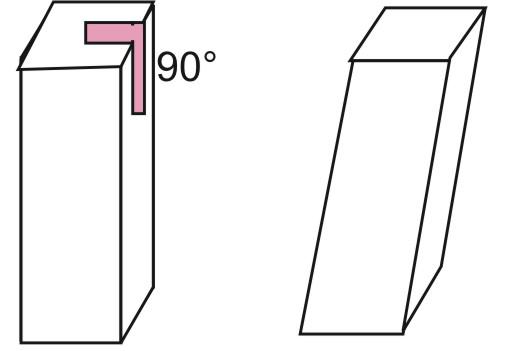
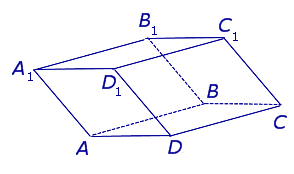
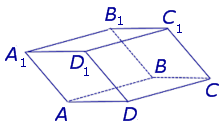
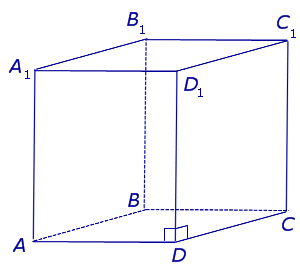
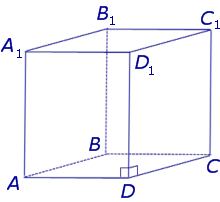
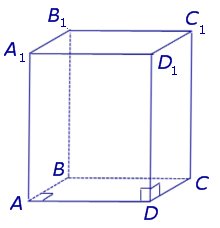
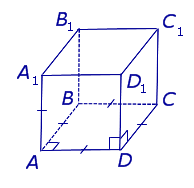
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
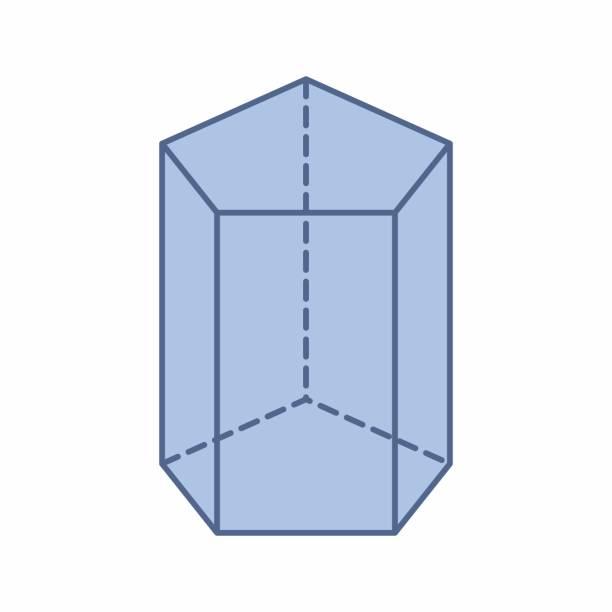
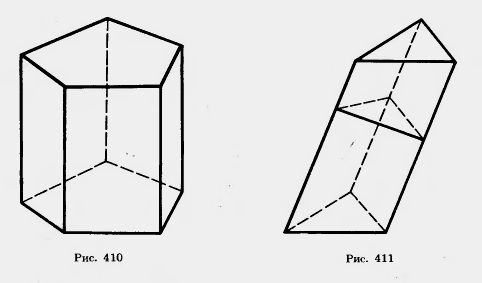
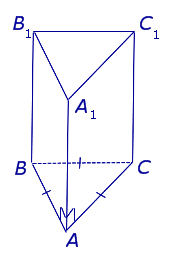
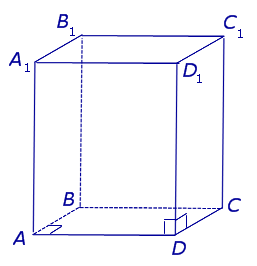
У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально (рис. 410).
Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 19.1. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Доказательство. Боковые грани прямой призмы — прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна
где a1,аn — длины ребер основания, р — периметр основания призмы, а I — длина боковых ребер. Теорема доказана.
Практическое задание
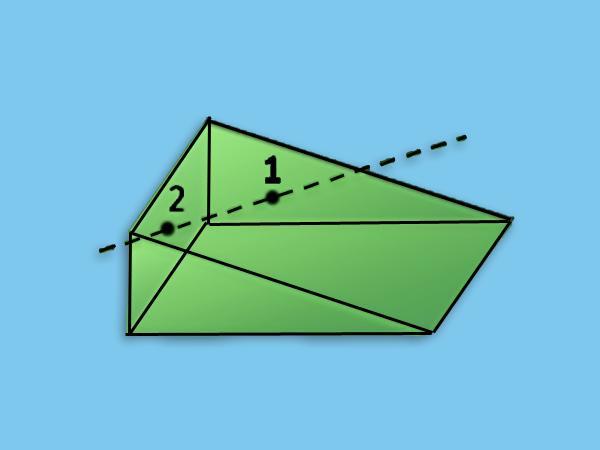
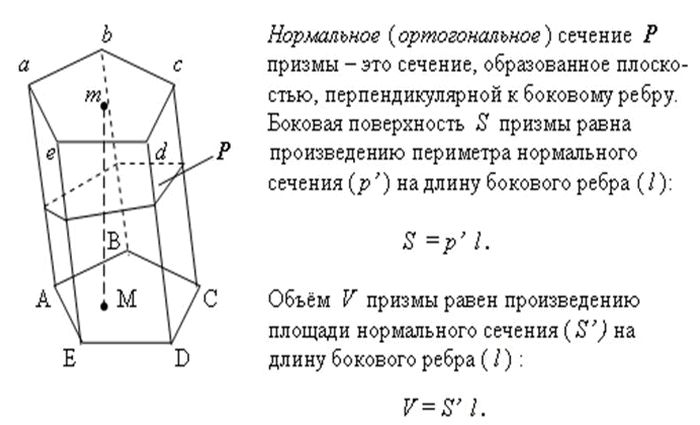
Задача (22). В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l.
Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
Обобщение пройденной темы
А теперь давайте попробуем с вами подвести итоги пройденной темы о призме и вспомним, какими свойствами обладает призма.
• Во-первых, у призмы все ее основания являются равными многоугольниками;
• Во-вторых, у призмы все ее боковые грани являются параллелограммами;
• В-третьих, у такой многогранной фигуры, как призма, все боковые ребра равны;
Также, следует вспомнить, что такие многогранники, как призмы могут быть прямыми и наклонными.
Какая призма называется прямой?
Если же у призмы боковое ребро расположено перпендикулярно плоскости ее основания, то такая призма носит название прямой.
Не будет лишним напомнить, что боковые грани прямой призмы являются прямоугольниками.
Какую призму называют наклонной?
А вот если же у призмы боковое ребро не расположено перпендикулярно плоскости ее основания, то можно смело утверждать, что это наклонная призма.
Какую призму называют правильной?
Если у основания прямой призмы лежит правильный многоугольник, то такая призма является правильной.
Теперь вспомним свойства, которыми обладает правильная призма.
Свойства правильной призмы
• Во-первых, всегда основаниями правильной призмы служат правильные многоугольники;
• Во-вторых, если рассматривать у правильной призмы боковые грани, то они всегда бывают равными прямоугольниками;
• В-третьих, если сравнивать размеры боковых ребер, то в правильной призме они всегда равны.
• В-четвертых, правильная призма всегда прямая;
• В-пятых, если же в правильной призмы боковые грани имеют форму квадратов, то такую фигуру, как правило, называют полуправильным многоугольником.
Сечение призмы
А теперь давайте рассмотрим сечение призмы:
Домашнее задание
А теперь давайте попробуем закрепить изученную тему с помощью решения задач.
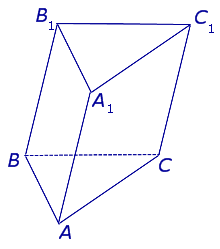
Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы.
Интересно знать
А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру.
У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы.
Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма.
Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Призма. Прямая призма. Правильная призма. Объем призмы
Факт 1. Про произвольную призму \(A_1. A_nB_1. B_n\)
\(\bullet\) Многоугольники \(A_1. A_n, \ B_1. B_n\) – основания;
отрезки \(A_1B_1, \ A_2B_2\) и т.д. – боковые ребра;
четырехугольники \(A_1B_1B_2A_2\) и т.д. – боковые грани, представляющие собой параллелограммы.
\(\bullet\) Высота призмы – расстояние между ее основаниями, или, что то же самое, – перпендикуляр, опущенный из вершины одного основания к плоскости другого основания.
\(\bullet\) \(<\color
\(\bullet\) Площадь боковой поверхности – сумма площадей ее боковых граней.
\(\bullet\) Площадь полной поверхности – сумма площади боковой поверхности и площадей оснований.
Факт 2. Про прямую призму
\(\bullet\) Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
\(\bullet\) Тогда:
1) боковые грани представляют собой прямоугольники;
2) боковое ребро является высотой призмы.
Факт 3. Про правильную призму
\(\bullet\) Призма называется правильной, если она прямая и ее основания – правильные многоугольники.
\(\bullet\) Тогда:
все боковые грани представляют собой равные прямоугольники.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Перечень вопросов, рассматриваемых в теме:
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
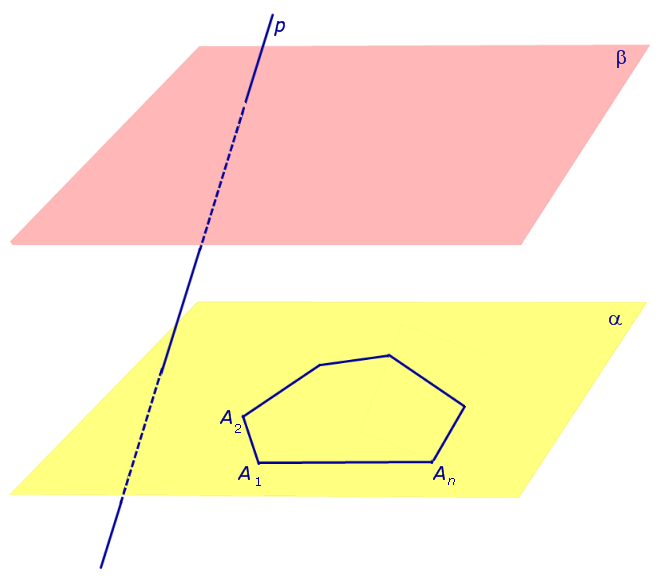
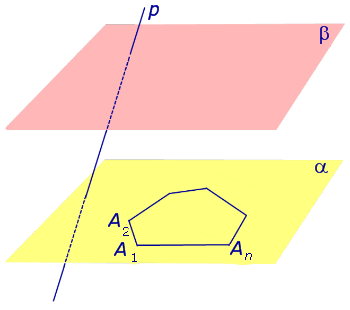
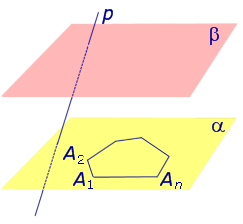
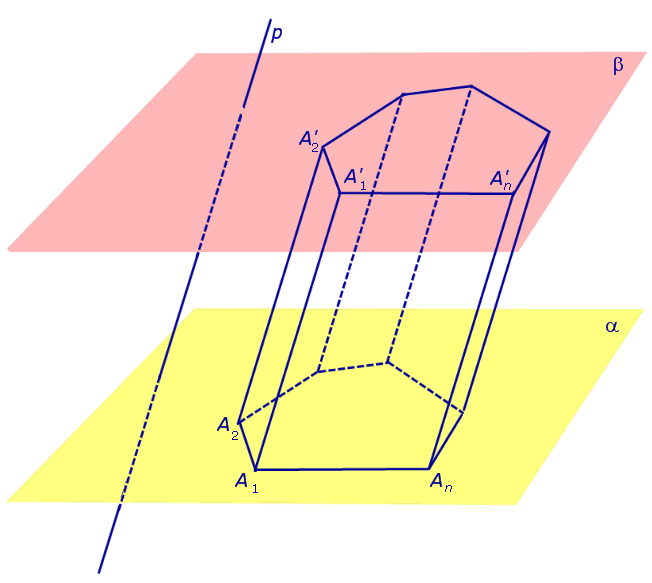
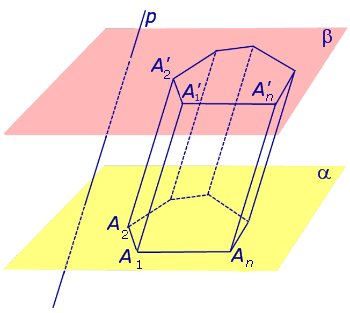
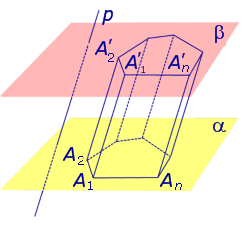
Рассмотрим два равных многоугольника А1А2. Аn и В1В2. Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
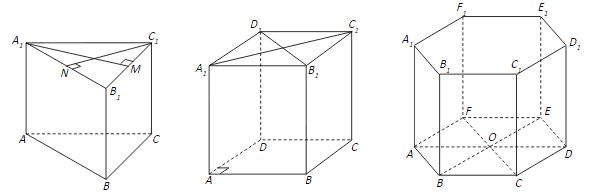
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
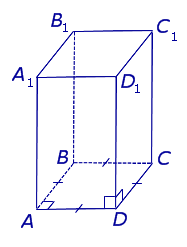
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С 2 =АА1 2 +АС 2 (1).
Так как в основании прямоугольник, то ВС=АD.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Найдите для каждой картинки пару
1)

4)
6)
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Призмы
Основные определения и свойства призм. Теорема Эйлера
Утверждение 1. Каждый из n четырехугольников
Для остальных четырехугольников доказательство проводится аналогично.
Это утверждение непосредственно вытекает из утверждения 1.
Замечание 1. В случае, когда не требуется делать специальных уточнений,
боковые грани и основания призмы называют гранями призмы
совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы,
n – угольные призмы называют призмами.
Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
то теорема Эйлера доказана.
Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
Виды призм. Прямые и наклонные призмы. Правильные призмы
Существует следующая классификация призм.
Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.
Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.
Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.