Как определить что функция ни четная ни нечетная
Четные и нечетные функции
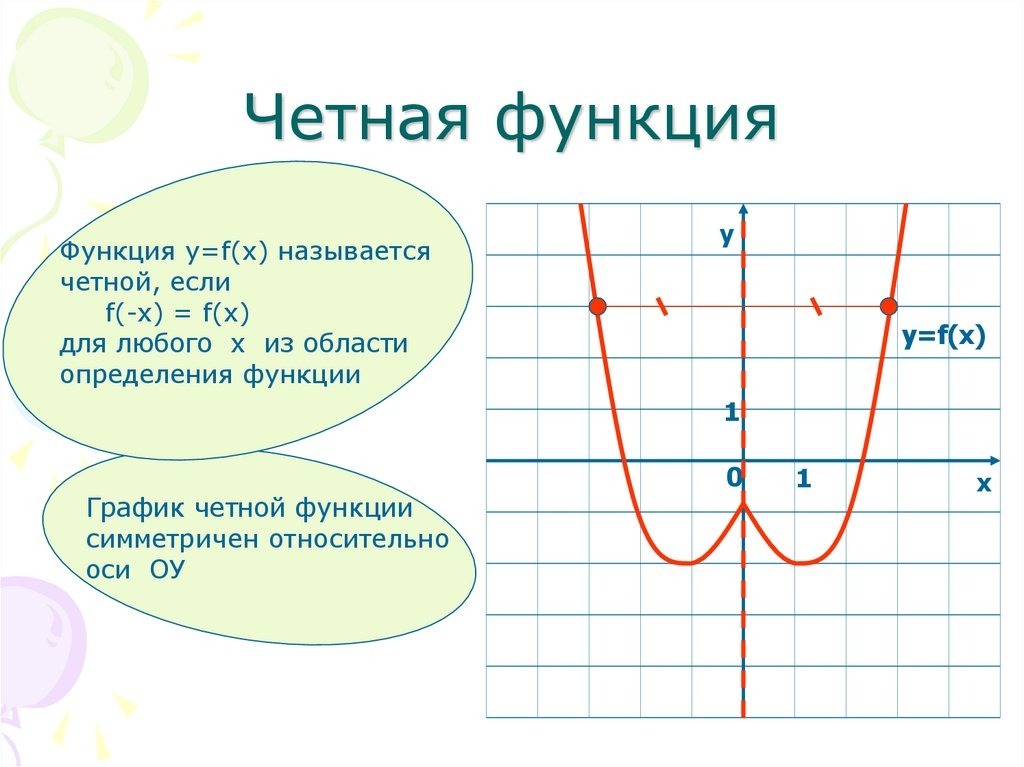
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
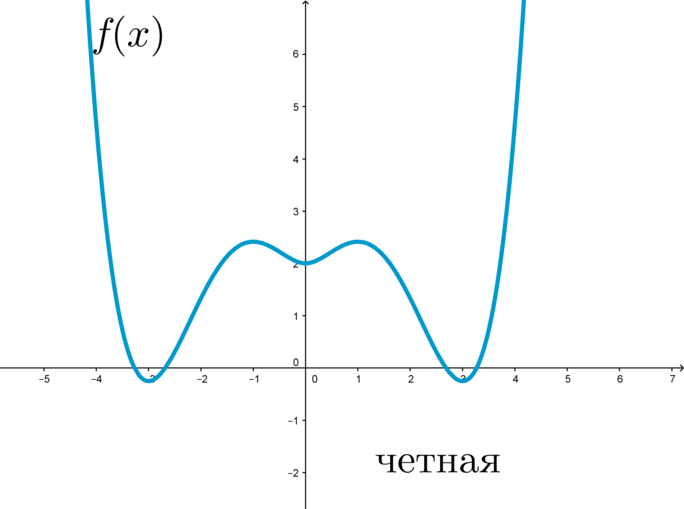
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
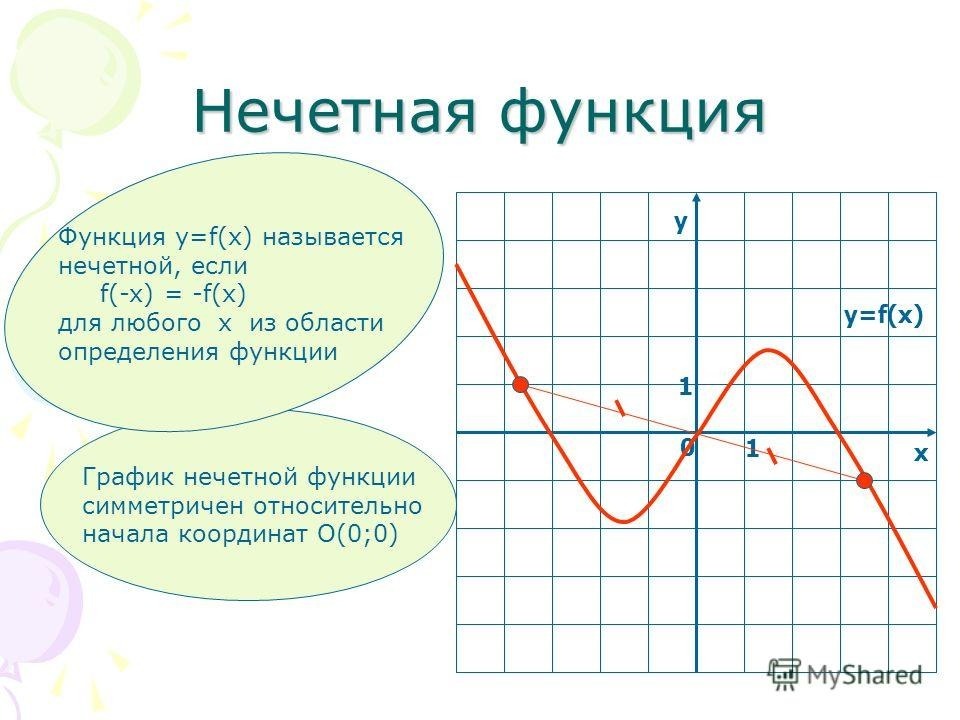
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
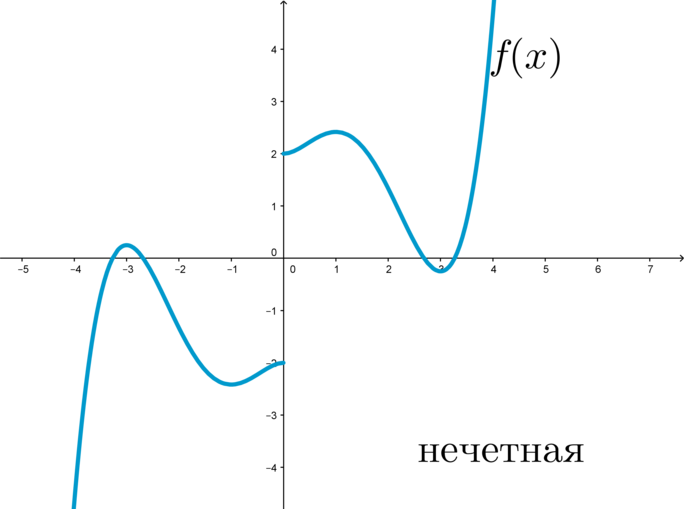
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
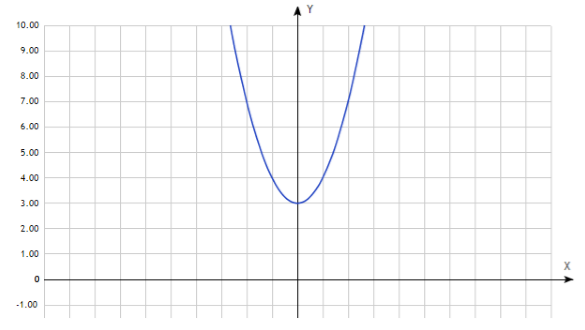
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
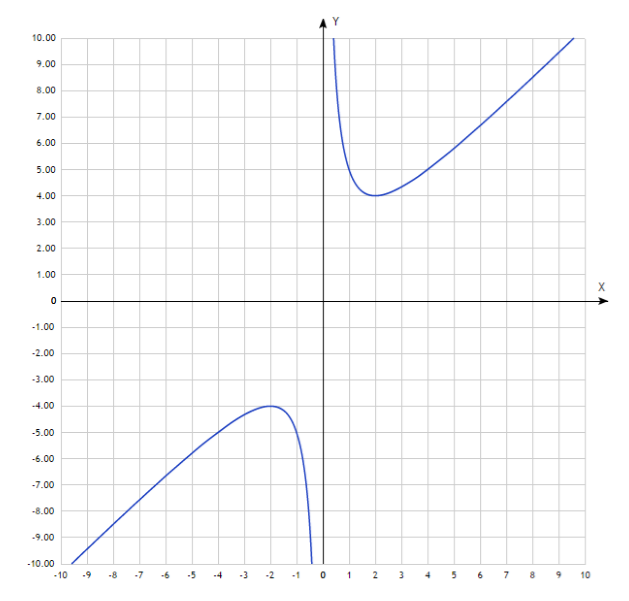
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
Четные и нечетные функции
График четной функции симметричен относительно оси \(y\) :
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
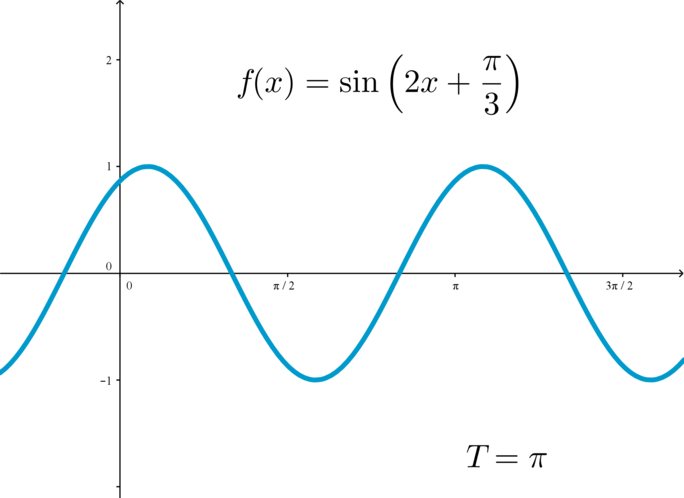
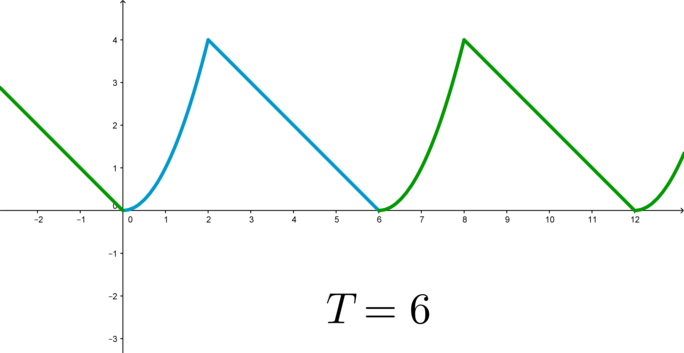
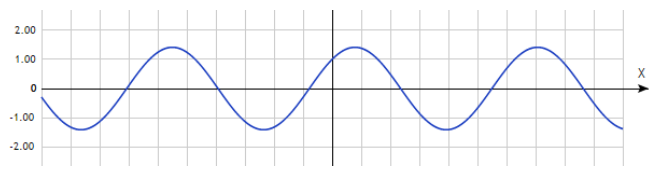
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
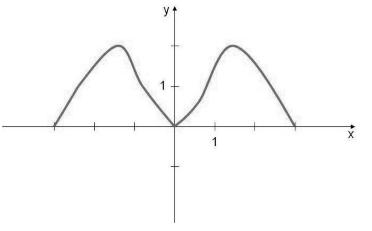
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
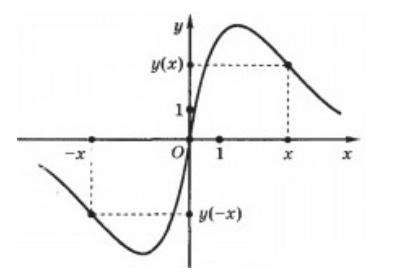
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
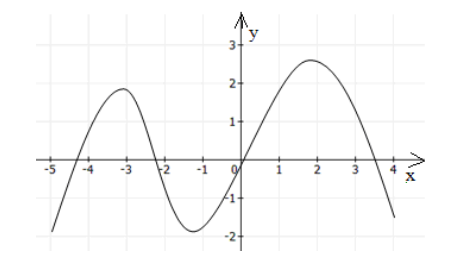
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021
Четность и нечетность функции
Определения и свойства четных и нечетных функций
\(\ f(x) \) называется четной функцией, если для любого x из области определения выполняется равенство \(\ f(-x)=f(x) \)
Функция \(\ f(x) \) называется нечетной функцией, если для любого x из области определения выполняется равенство \(\ f(-x)=-f(x) \)
Если ни одно из условий \(\ f(-x)=f(x) \) или \(\ f(-x)=-f(x) \) не выполняется, то говорят, что функция \(\ f(x) \) не является ни четной, ни нечетной (или функцией общего вида)
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
При исследовании функции на четность и нечетность можно использовать следующие свойства:
1.Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
2.Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.
3.Если функция \(\ f(x) \) четная (нечетная), то и функция \(\ \frac<1>
Примеры решения задач
Используя определение исследовать на четность и нечетность следующие функции
1) Рассмотрим значение функции \(\ f_<1>(x)=2 x^<4>-3 x^<2>+6 \) в точке \(\ (-x) \) :
2) Найдем значение функции \(\ f_<2>(x)=8 x^<3>-7 x \) в точке \(\ (-x) \) :
Для этой функции выполняется условие \(\ f_<2>(-x)=-f_<2>(x) \),следовательно, она является нечетной.
3) Найдем значение функции \(\ f_<3>(x)=x^<4>-4 x+5 \) в точке \(\ (-x) \) :
2) \(\ f_<2>(x)=8 x^<3>-7 x \) — нечетная;
3) \(\ f_<3>(x)=x^<4>-4 x+5 \) — ни четная, ни нечетная.
Исследовать функцию \(\ f(x)=\frac
Исследуем отдельно четность функции, которые находятся в числителе и знаменателе:
то есть функция \(\ g(x) \) четная; аналогично
а тогда и функция \(\ h(x) \) четная.