Как определить что функция симметрична

Четные и нечетные функции

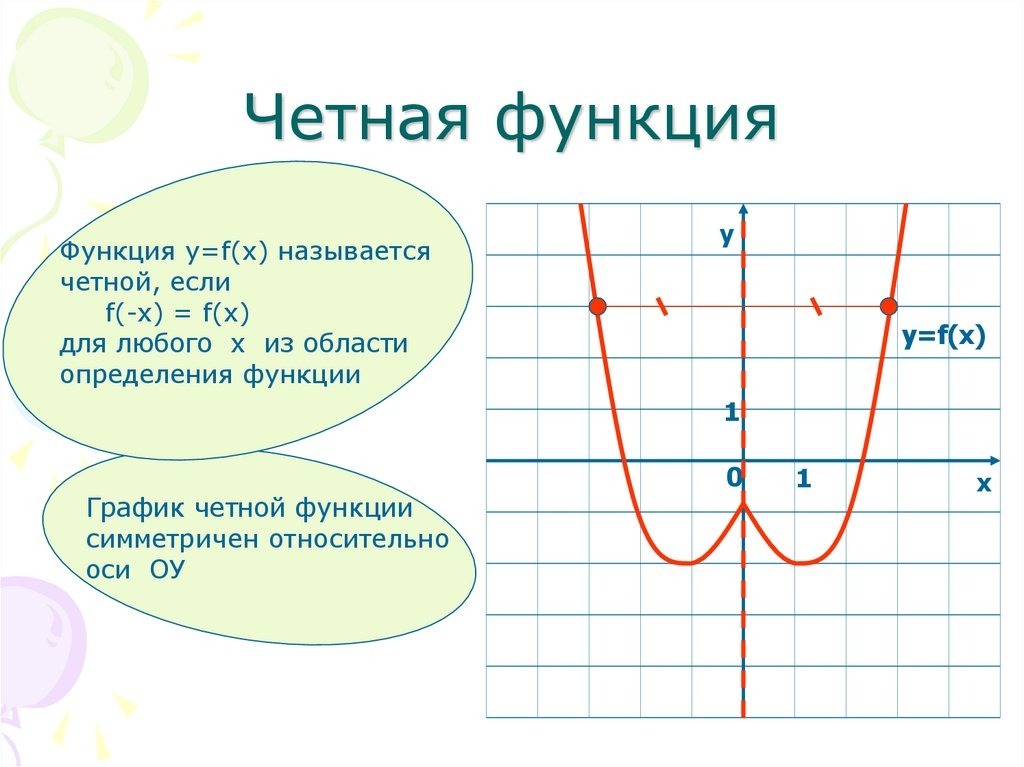
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График четной функции симметричен относительно оси ординат.

Например, — четные функции.

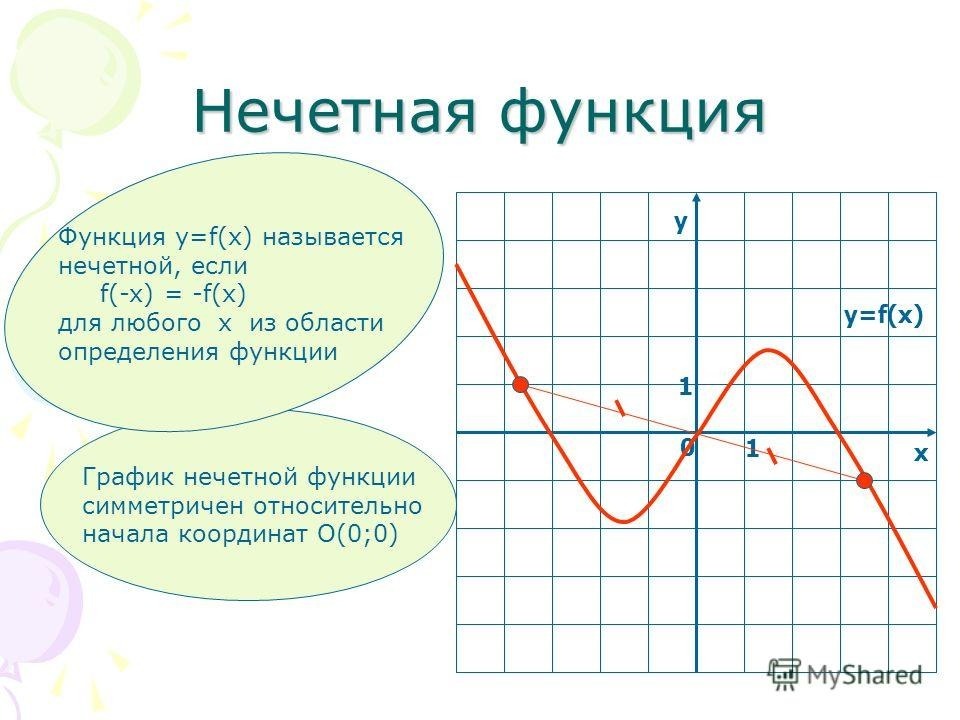
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График нечетной функции симметричен относительно начала координат.

Например, — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция четной (нечетной).

Область определения функции

Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.

— значит, функция нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция четной (нечетной)

Область определения: все действительные числа.

— чётная, как сумма двух чётных функций.

Её график симметричен относительно оси y.

3. Проверьте, является ли функция четной (нечетной).

Область определения функции симметрична относительно нуля.

— чётная, её график симметричен относительно оси y.

Источник

Понятие четной и нечетной функции

Понятие четности и нечетности функции

Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.

Четная функция

Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

График четной функции симметричен относительно оси Ох.

Нечетная функция

Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)

График нечетной функции симметричен относительно начала координат (точки (0;0)).

Произведение четной и нечетной функции

Произведение четной и нечетной функций есть нечетная функция.

Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)

Исследование функций в примерах

Доказать, что функция \(y=x^2\) четная.

1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)

1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)

Рассмотрим первую функцию:

1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.

Рассмотрим вторую функцию:

Источник

Презентация по математике «Симметрия в построении графиков функции»

XVI научная конференция молодых исследователей «Шаг в будущее»

Симметрия в построении графиков функции

Автор : Шматова Алёна Сергеевна, ученица 10 «А» класса, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44

Научный руководитель: Шибко Елена Николаевна, учитель математики, Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №44

Содержание

Аннотация

Данная исследовательская работа направлена на изучение использования симметрии в жизни человека и математических науках; изучение теоретической стороны темы; проведение практической работы по теме «Симметрия». Изучив проблему симметрии, мы увидели, что симметрия присутствует и в прошлом, и в настоящем, и в будущем. Симметрия – это не только математическое понятие. Его заимствовали из природы. А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, передаётся генетически из поколения в поколение.

Введение

Симметрия… является той идеей, посредством

которой человек на протяжении веков пытался

постичь и создать порядок, красоту и

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.

Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей. Его широко используют все без исключения направления современной науки.

Об этой закономерности задумывались многие великие люди. Например, Л.Н. Толстой говорил: «Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врождённое чувство. На чём же оно основано?»

Симме́три́я (др.-греч. συμμετρία — «соразмерность»), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

узнать где и как используется симметрия в жизни человека.

Выяснить, кто первым обратил внимание на использование симметрии в жизни человека.

Выявить где используется центральная симметрия.

Выявить где используется осевая симметрия.

Выяснить, как легче строить графики симметричных функций.

Выявить, можно ли наблюдать симметрию в неживой природе.

Проанализировать симметрию в природе и связь природы с математикой.

Определить связь между симметрией в природе, математики, физике, архитектуры.

Выявить симметричные функции.

Доказать, что существуют такие функции, которые связанны с природой.

Гипотеза: Симметрия существует в природе, математики, физике, архитектуре.

Объект исследования: симметрия в природе, математики, физике, архитектуре.

Методы исследования: изучение, анализ и обобщение данных научной литературы, наблюдение, фотографирование, анкетирование, интервьюирование, эксперимент, количественный и качественный учет данных, обработка и анализ полученных данных.

Глава 1. Симметрия

Симметрия является той идеей, посредством которой человек на протяжении веков пытался

постичь и создать порядок, красоту и

Формы восприятия и выражения во многих областях науки и искусства, в конечном счёте, опираются на симметрию, используемую и проявляющуюся в специфических понятиях и средствах, присущих отдельным областям науки и видам искусства.

Действительно, симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.

Весь мир можно рассмотреть как проявление единства симметрии и асимметрии. Асимметричное в целом сооружение может являть собой гармоничную композицию из симметричных элементов.

Симметрия многообразна, вездесуща. Она создает красоту и гармонию.

Идея симметрии часто является отправным пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии.

Глава 2. Виды симметрии

«симметрией» в математике понимается такое преобразование пространства (плоскости), при котором каждая точка M переходит в другую точку M’ относительно некоторой плоскости (или прямой), когда отрезок MM’ является перпендикулярным плоскости (или прямой) и делится ею пополам. Плоскость (прямая) называется при этом плоскостью (или осью) симметрии.

Осью симметрии L называется такая прямая линия, вокруг которой симметричная фигура может быть повернута несколько раз таким образом, что каждый раз фигура «самосовмещается» сама с собой в пространстве. Число таких поворотов вокруг оси

Наконец, центром симметрии C называется такая особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через точку прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) точки фигуры. «Идеальным» примером такой фигуры является шар, центр которого и является его центром симметрии.

Симметрия широко встречается в объектах живой и неживой природы. Например, симметрия в химии отражается в геометрической конфигурации молекул. Так, например, молекула метана СH4 обладает симметрией тетраэдра. Понятие «симметрии» является центральным при исследовании кристаллов. При этом симметрия внешних форм кристаллов определяется симметрией его атомного строения, которая обуславливает и симметрию физических свойств кристалла.

Особенно широко понятие «симметрии» применительно к физическим законам используется в современной физике. Если законы, устанавливающие соотношения между величинами или определяющие изменение этих величин со временем, не меняются при определенных операциях (преобразованиях), которым может быть подвергнута система, то говорят, что эти законы обладают симметрией (или инвариантны) относительно данных преобразований. Например, закон тяготения действует в любой точки пространства, то

есть он является инвариантным по отношению переноса системы как целого в пространстве.

На явление симметрии в живой природе обратили внимание еще пифагорейцы в связи с развитием ими учения о гармонии. Установлено, что в природе наиболее распространенной «Зеркальной» симметрией обладает бабочка, листок или жук (Рис.2) и часто такой вид симметрии называется «симметрией листка» или «билатеральной симметрией». К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево и часто такой вид симметрии называется «ромашко-грибной» симметрией.

Рис.2

Еще в 19-м веке исследования в этой области привели к заключению, что симметрия природных форм в значительной степени зависит от влияния сил земного тяготения, которое в каждой точке имеет симметрию конуса. В результате был найден следующий закон, которому подчиняются формы природных тел:

Все то, что растет или движется по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой («ромашко-грибной») симметрии (рис.3б). Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии – «симметрии листка» (одна плоскость симметрии) рис.3а.

рис.3б радиально-лучевая симметрия

Принцип симметрии очень часто используется совместно с принципом «золотого сечения». Таким примером может служить картина Рафаэля «Обручение Марии».

Глава 3. Симметрия в построении графиков функции.

Две точки А и А называются симметричными относительно точки О, если О – середина отрезка АА . Точка О считается симметричной самой себе.

Точка М называется симметричной точке М относительно прямой а, если прямая ММ перпендикулярна прямой а и МО = ОМ , где О — точка пересечения прямых ММ и а.

Преобразование фигуры F в фигуру F , при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии.

Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.

Свойство 1. График четной функции симметричен относительно оси ОУ.

Доказательство. Пусть y= f(x) — четная функция, тогда f(-x) = f(x). Рассмотрим произвольную точку графика M(x ; f(х )) и точку М (- x ; f (- x )). Так как функция

у = f(х) — четная, то f( х ) = f (-х ) =>вторые координаты точек М и M равны. Точки графика М и M симметричны относительно оси ОУ. Так как М — произвольная точка графика, то, значит, график четной функции симметричен относительно оси ОУ.

Свойство 2. График нечетной функции симметричен относительно начала координат.

Точки графика М и M симметричны относительно начала координат. Так как М —произвольная точка графика, то, значит, график четной функции симметричен относительно начала координат.

а) у=х

Докажем, что ось ОУ является осью симметрии данного графика.

у(-а) = (-а) = а , y(a) = a => y(a) = y(-a) => y = x — четная функция (определение 1) => ось ОУ является осью симметрии данного графика.

Докажем, что никакая другая прямая не будет являться осью симметрии.

Предположим, что некоторая прямая х = х является осью симметрии, тогда

у (x + a) = (x +а) = х + 2х а + а => y(x + a) у(x –a) => у(x –a) = (x +а) =

= х — 2х а + а

прямая х = х не является осью симметрии данного графика.

б) y= ax + bx + c.

Докажем, что для данного графика ось симметрии будет проходить через вершину параболы (x ; y ) параллельно оси ОУ.

Первую координату вершины параболы можно вычислить по формуле:

. Рассмотрим произвольную точку графика M(x +а; у (х +а)) и точку

М (x — а; у ( x — а)).

у(x +а) = а(x +а) + b(x +а)+с = а x + 2а x + а + bx + аb + с =

Значит, точки М и М симметричны относительно прямой, проходящей через вершину параболы y= ax + bx + c. Следовательно, график данной функции симметричен относительно прямой

в) у= х .

Докажем, что начало координат будет точкой симметрии данного графика.

симметрии данного графика является начало координат (доказательство 2).

Графиком данной функции является прямая.

1. Каждая точка, принадлежащая этой прямой, будет являться ее центром симметрии, т.е. у этого графика бесконечно много центров симметрии.

Рассмотрим точку М(x ;y ). Пусть M ( x ; y )—точка графика данной функции, отличная от точки М, а точка М такая точка графика, что М M =М М . Тогда первая координата

точки М равна 2 x — x . Убедимся, что точка М принадлежит графику данной функции.

у = k(2 x — x )+ b

y= 2kx — k х +b

Следовательно, точка М принадлежит графику функции.

Осью симметрии данного графика будет являться прямая параллельная оси ОУ и проходящая через некоторую координату (x ; 0), которая принадлежит графику функции.

у(-х) = k|-x|+b = k|x| + b = у(х) => функция y = k|x| + b является четной (определение 1) Значит, она симметрична относительно оси ОУ.

з)y = а + b│х│+с.

у(-х) = а(-х) + b│-х│+с = ах + b│х│+с = у(х). => ось ОУ является осью симметрии данного графика.

и) y=│ax +bx+c│

Так же мы знаем, что через вершину параболы ( х ; у ) проходит прямая, параллельная оси ординат, которая является осью симметрии параболы.(2)

Из свойств (1) и (2), следует, что ось симметрии параболы является осью данного графика.

Заключение

С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Существует множество видов симметрии, как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.

Симметрия в алгебре и геометрии имеет большое значение. Я рассмотрела основные теории, связанные с симметрическими системами уравнений. Научилась решать симметрические системы уравнений, и узнала кое-что новое про симметрию графиков функций. Выбранная тема актуальна, так как в средней школе не рассматриваются все виды симметрий в алгебре и геометрии.

Источник