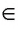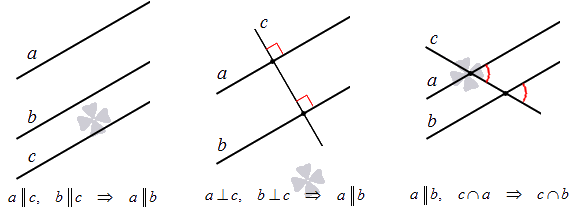Как показать что прямые не имеют общих точек

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

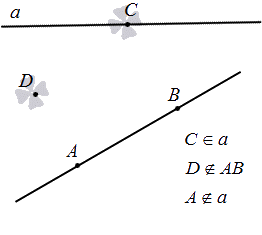
Опишем взаимное расположение точек и прямой.

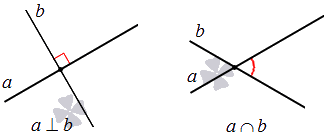
Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

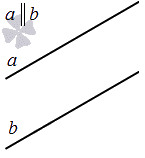
Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

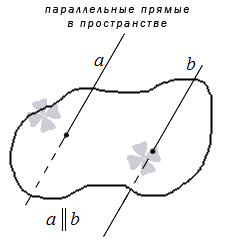
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

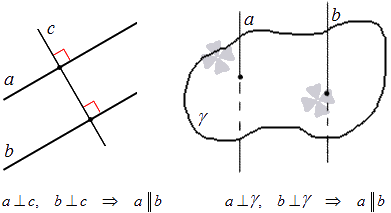
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

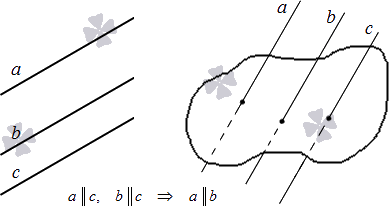
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

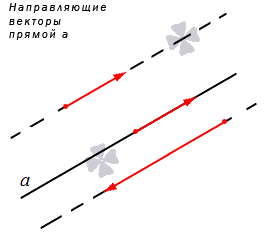
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

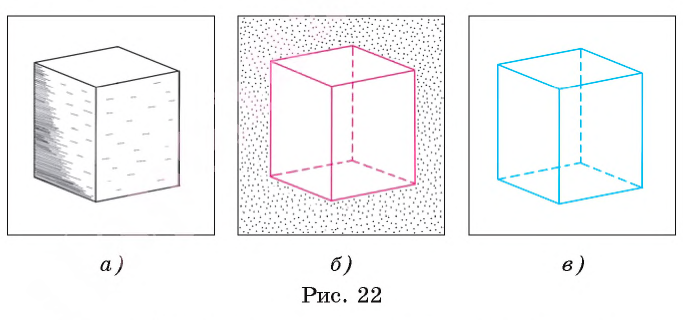
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 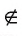b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

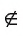
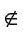
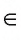
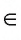
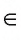
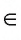
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

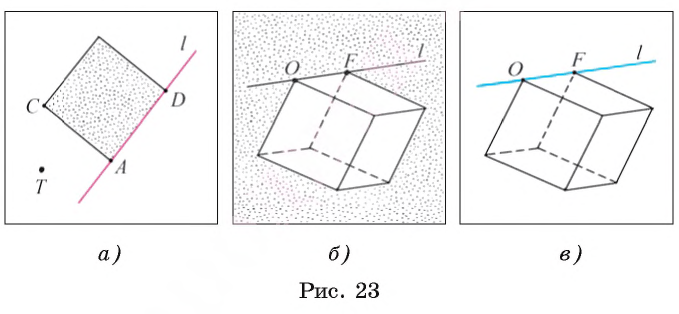
Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

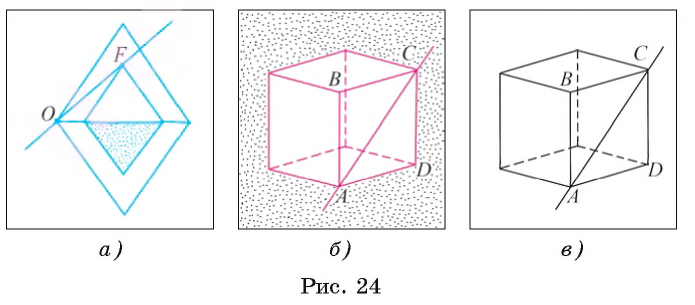
Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 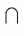ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 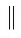l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС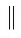АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Прямая на плоскости – необходимые сведения

Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.

Прямая на плоскости – понятие

Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.

Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.

Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.

Взаимное расположение прямой и точки

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Точка делит прямую на две части, называемые лучами. Имеем аксиому:

Взаимное расположение прямых на плоскости

Расположение прямых на плоскости может принимать вид двух состояний.

Две прямые на плоскости могут совпадать.

Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.

Две прямые на плоскости могут пересекаться.

Две прямые на плоскости могут быть параллельны.

Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.

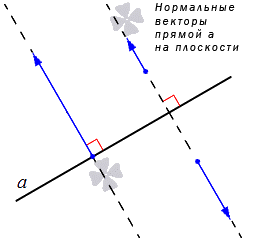
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.

Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.

Для этого приводим необходимы факторы, доказывающие их взаимное расположение:

Рассмотрим это на рисунках.

Способы задания прямой на плоскости

Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.

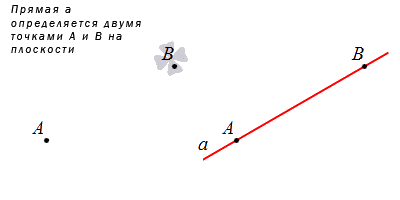
Прямая задается при помощи указанных двух точек, расположенных в плоскости.

Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.

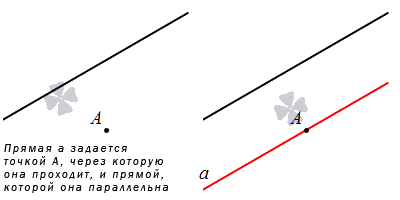
Прямая может быть задана через точку и прямую, которой она параллельна.

Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.

Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.

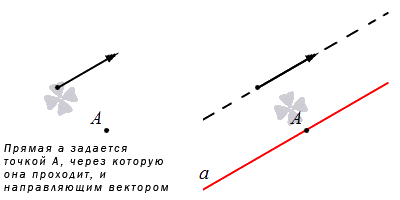
Прямая задается через указанную точку и направляющий вектор.

Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.

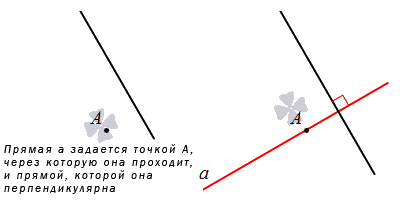
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:

Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.

И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.

Источник