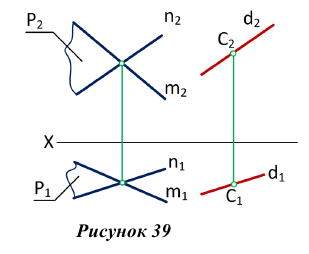
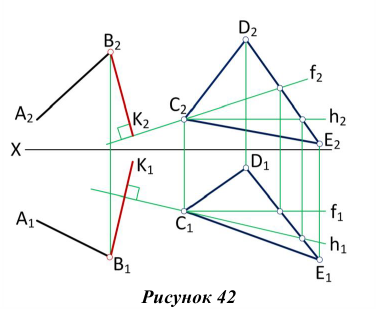
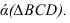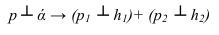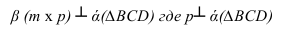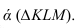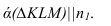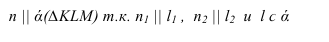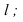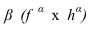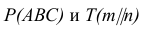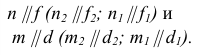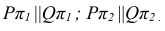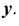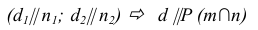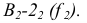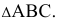Как записать что прямая лежит в плоскости
Прямая на плоскости – необходимые сведения.
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.
Теперь можно переходить и к понятию прямой линии на плоскости.
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Взаимное расположение прямой и точки.
Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.
Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В ), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА ).
Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Взаимное расположение прямых на плоскости.
Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?
Во-первых, две прямые на плоскости могут совпадать.
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться.
В-третьих, две прямые на плоскости могут быть параллельными.
Две прямые на плоскости называются параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение 
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой. В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой. О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости.
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
Способы задания прямой на плоскости.
Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Во-первых, прямую можно задать, указав две точки на плоскости.
Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.
Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки.
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.
Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.
Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости.
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.
Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.
Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой.
Взаимное положение прямой и плоскости с примерами
Содержание:
Проекции прямого угла:
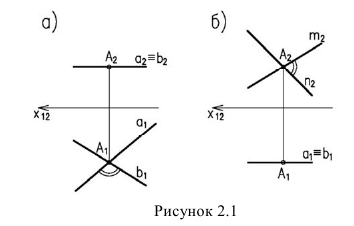
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).
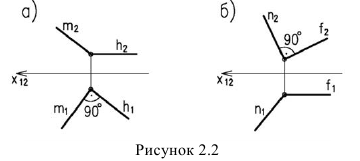
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).
Взаимное положение примой и плоскости, двух плоскостей
Прямая относительно плоскости может занимать следующие положения: лежать в плоскости (что рассматривалось ранее); быть ей параллельна; пересекать плоскость; быть перпендикулярной плоскости (т.е. пересекать под прямым углом).
Две плоскости могут быть:
Перпендикулярность примой и плоскости
Условие перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.
Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронгали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.
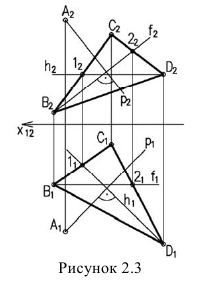
На рисунке 2.3 через точку 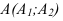
В плоскости 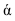
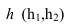
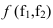
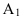
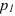
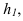
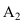
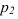
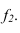
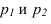
Перпендикулярности двух плоскостей
Две плоскости взаимно перпендикулярны, если одна из них содержи! перпендикуляр к другой.
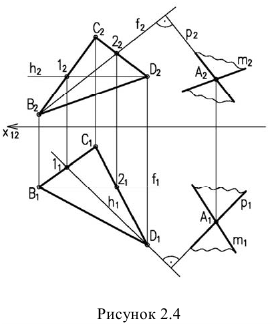
Пусть через данную прямую т необходимо провести плоскость, перпендикулярную плоскости а. заданной треугольником 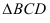
Для решения задачи достаточно на прямой т взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости 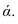
Пересекающиеся прямые m и р образуют плоскость 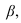
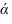
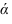
Параллельность прямой и плоскости
Условие параллельности прямой и плоскости:
Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.
Рассмотрим пример решения задачи на параллельности прямой и плоскости.
Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной
Для решения задачи:
Проводим горизонтальную проекцию прямой 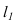
Строим фронтальную проекцию
Через точку 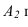
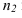
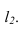
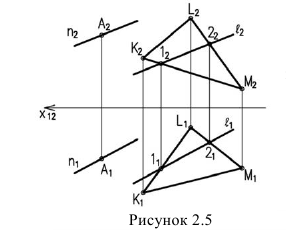
Параллельность двух плоскостей
Условие параллельности двух плоскостей:
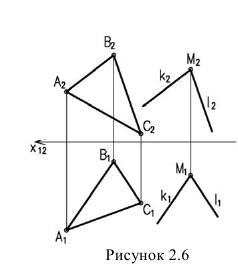
Изображенные на рисунке 2.6 плоскости 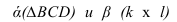
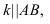
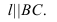
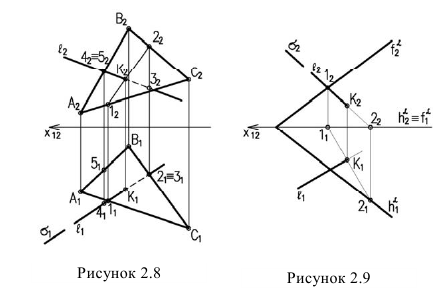
Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертательной геометрии.
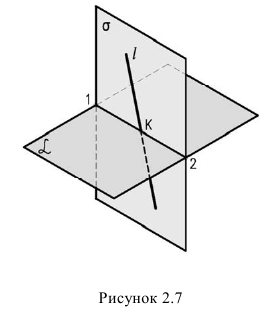
Алгоритм решения задачи (рисунок 2.7):
1. Прямую 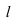
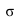
2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной
3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой
4. Определяем видимость прямой 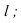
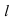
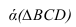
Пересечение двух плоскостей
Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.
Рассмотрим несколько случаев построения линии пересечения двух плоскостей.
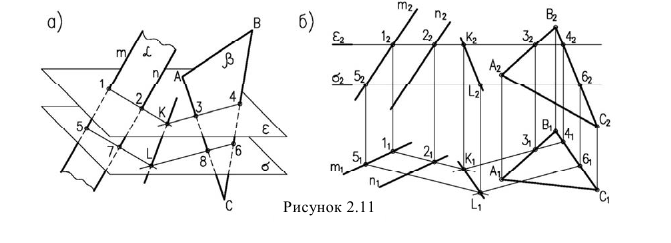
Задача сводится к нахождению точек пересечения прямых m и n с плоскостью а. 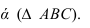
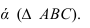
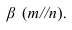
Алгоритм решения задачи (рисунок 2.11):
Видимость при этом не определяется.
В данном случае в качестве плоскостей-посредников могут быть использованы плоскость проекций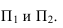
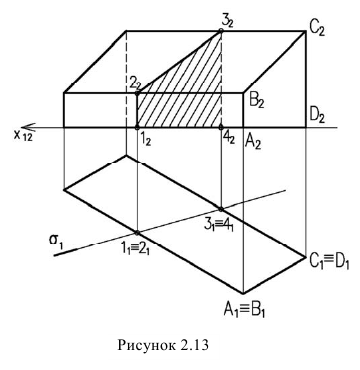
Пересечение многогранника проецирующей плоскостью
Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью о (рисунок 2.13)
Взаимное положение двух плоскостей
Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться.
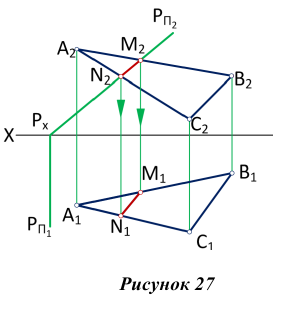
Пересечение плоскости общего положения с плоскостью частного положения
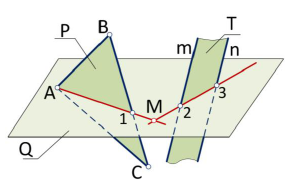
На рис. 27 показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника AВС.
Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция 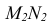
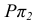
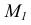
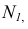
Пересечение двух плоскостей общего положения
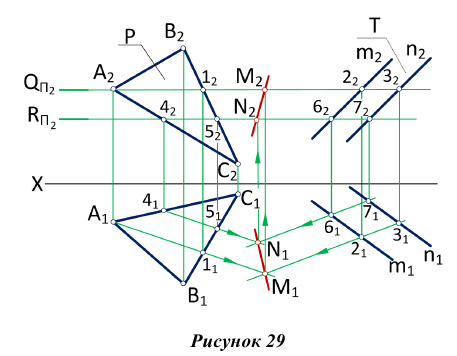
Задача. Построить линию пересечения двух плоскостей общего положения
Алгоритм решения задачи (рис. 28)
Плоскости параллельны
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
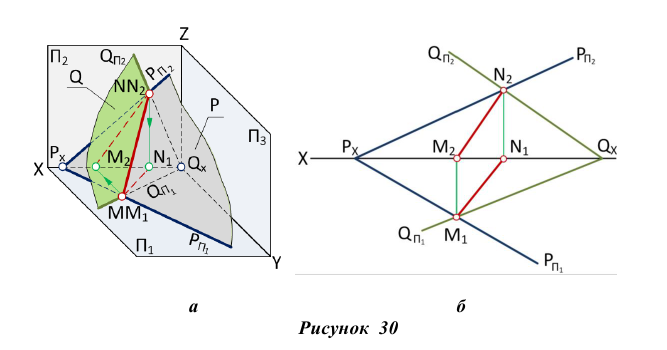
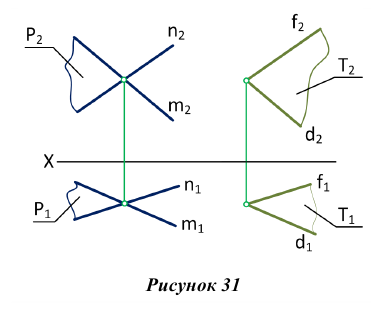
Изображенные на рис. 31 плоскости 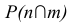
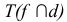
Плоскости общего положения также параллельны, если два любых одноименных следа параллельны между собой.
Изображенные на рис. 32 плоскости Р и Q параллельны, т.к.
Взаимное положение прямой линии и плоскости
Прямая может лежать в плоскости, пересекать плоскость и быть параллельной плоскости.
Пересечение прямой линии с плоскостью частного положения
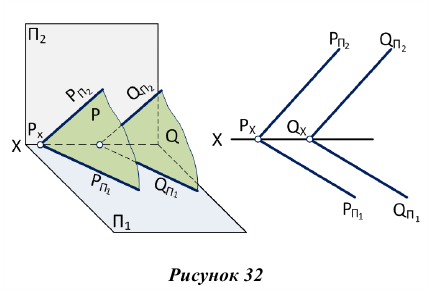
Если заданная плоскость перпендикулярна к какой-либо плоскости проекций (рис.33, а), то она проецируется на эту плоскость проекций в виде прямой линии, на которой обязательно будут находиться соответствующие проекции всех точек, принадлежащих данной плоскости, в том числе и проекции точки пересечения какой-то прямой с заданной плоскостью (точка встречи прямой с плоскостью). Поэтому точка встречи прямой с плоскостью частного положения находится па эпюре без дополнительных построений (рис. 33,6).
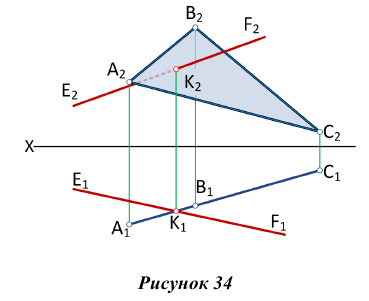
На рис. 34 точка встречи прямой EF с горизонтально-проецирующей плоскостью, заданной треугольником ABC, является точкой пересечения горизонтальных проекций 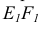
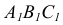
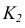
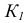
Определение видимости на эпюрах
Вопрос о видимости линий или поверхностей всегда может быть сведен к вопросу о видимости точек. Если несколько точек находятся на общей для них линии связи, то видимой будет только одна из них — наиболее удаленная от той плоскости проекций, по отношению к которой определяется видимость.
Точки, расположенные на одной линии связи, называются конкурирующими. Точки А, В и С, D — конкурирующие (рис. 35).
Относительно плоскости проекций 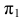
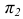
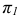
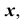
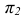
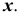
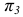
Пересечение прямой линии с плоскостью общего положения
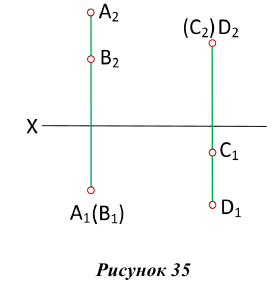
Точку пересечения прямой линии АВ с плоскостью общего положения Р (рис. 36) находят следующим образом:
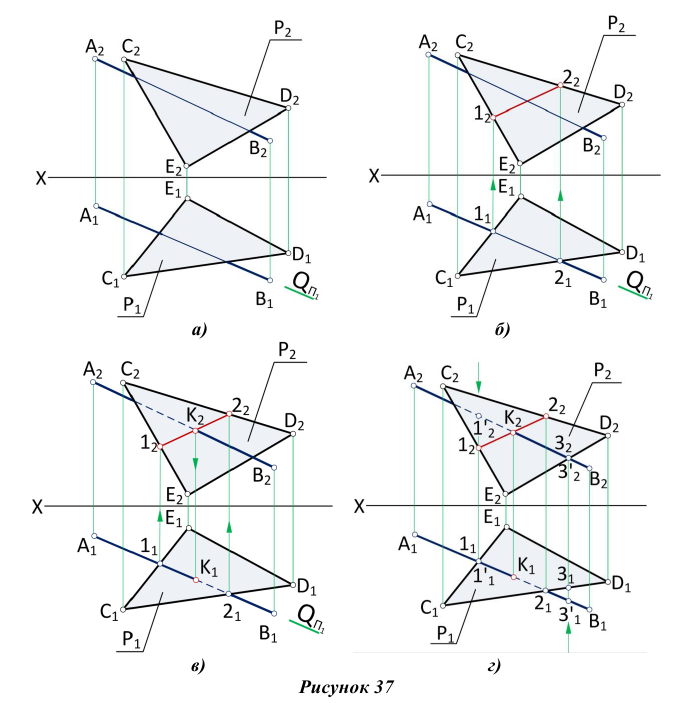
Пошаговые построения по определению точки пересечения прямой АВ с плоскостью треугольника CDE на эпюре приведены на рис. 37 (а-в).
Аналогично, используя конкурирующие точки 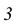
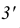
Задачи, на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение прямой с плоскостью.
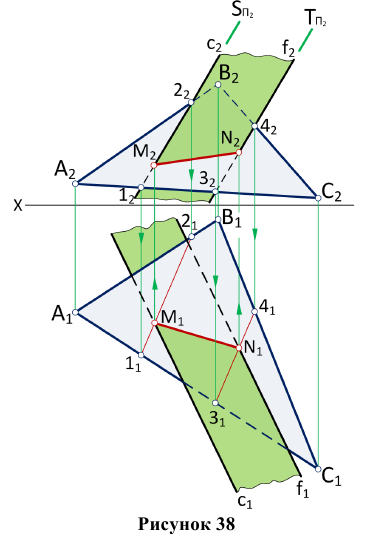
Одна из изображенных на рис. 38 плоскостей задана треугольником AВС, а вторая — двумя параллельными прямыми с и f.
Точка N найдена аналогично. Прямая MN — искомая. Видимость на рис. 86 определена из условия, что заданные плоскости ограничены треугольником и двумя параллельными прямыми, определяющими их.
Прямая параллельна плоскости
На рис. 39 через точку С проведена прямая d, параллельная плоскости Р, заданной пересекающимися прямыми т и п.
Прямая d параллельна прямой n, принадлежащей плоскости 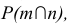
Прямая перпендикулярна плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Чтобы построить перпендикуляр из точки D на плоскость треугольника AВС (рис.40) необходимо предварительно построить
горизонталь 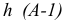
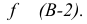
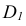
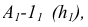
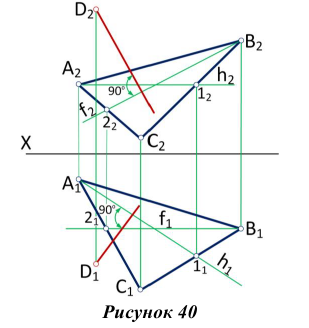
Если же плоскость задана следами, то, учитывая, что фронтальная проекция любой фронтали в этой плоскости всегда параллельна фронтальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 41), что проекции перпендикуляра к плоскости должны быть перпендикулярны соответствующим следам плоскости.
Плоскости перпендикулярны
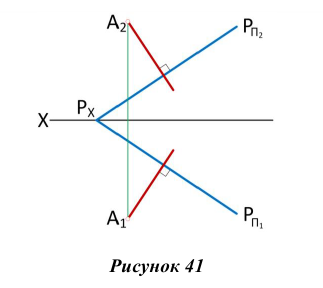
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. На рис. 42 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой АВ восстановлен перпендикуляр ВК к плоскости треугольника 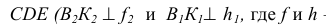
Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.
Задача.
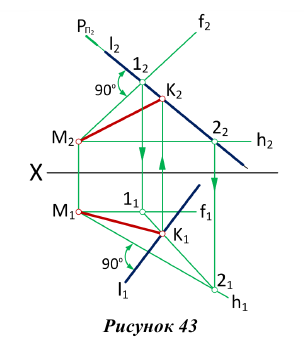
Через точку М провести прямую, перпендикулярную прямой
Для построения взаимно перпендикулярных прямых (рис. 43), одна из которых 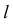
Задача:
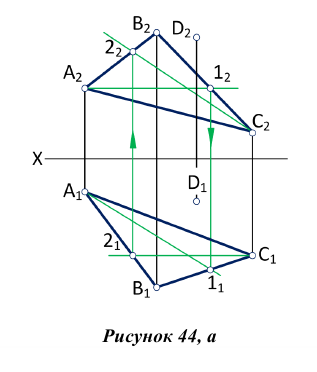
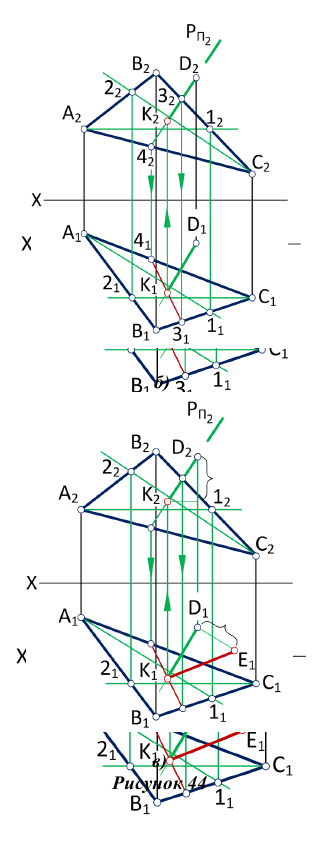
Определить расстояние от точки до плоскости, заданной треугольником ABC (рис.44)
Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:
1. Из точки D опускаем перпендикуляр на плоскость треугольника AВС (рис.44, а), для этого в плоскости треугольника проводим горизонталь 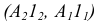
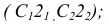
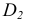
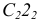
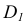
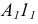
2. Находим точку пересечения перпендикуляра с плоскостью 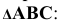
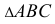
3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости 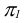
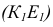
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.