Кубик бросается 5 раз найти вероятность что шестерка выпадет 2 раза

6.3. Решение задач

Пример 1. Игральную кость подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет: а) два раза; б) хотя бы один раз.

Решение. Проводится 10 независимых испытаний. Каждое испытание имеет два исхода: шестерка выпадет, шестерка не выпадет. Вероятность выпадения шестерки в каждом испытании постоянна и равна . Таким образом, мы имеем дело со схемой Бернулли.

Для нахождения искомых вероятностей воспользуемся формулой Бернулли (13) и формулой (14) соответственно.

А) Здесь n = 10, m = 2, , . Тогда по формуле (4.1) .

Б) По формуле (14) найдем, что .

Пример 2. Всхожесть семян данного сорта растений составляет 70 %. Найти наивероятнейшее число всхожих семян в партии из 240 семян.

Решение. Наивероятнейшее число всхожих семян находим из условия (15). Поскольку n = 240, p = 0,7 и q = 0,3, то , т. е. . Отсюда следует, что .

Пример 3. В урне 10 красных и 40 синих шаров. Вынимают подряд 14 шаров, причем цвет вынутого шара регистрируют, а затем шар возвращают в урну. Определить наивероятнейшее число появлений красного шара

Решение. Здесь , , . Используя двойное неравенство (15) при указанных значениях n, p и q, получим ,

Т. е. . Таким образом, задача имеет два решения: , .

Пример 4. По мишени, состоящей из внутреннего круга и двух концентрических колец, производится 10 выстрелов из спортивного пистолета. Вероятности попадания в указанные области при каждом выстреле равны соответственно 0,15; 0,22 и 0,13. Определить вероятность того, что при этом будет шесть попаданий в круг, три – в первое кольцо и одно попадание во второе кольцо.

Решение. Пусть событие — попадание в круг при одном выстреле, — попадание в первое кольцо, — попадание во второе кольцо. По условию , , . Всего производится опытов. Определяется вероятность P того, что при этих опытах событие произойдет шесть раз, событие — три раза и событие — один раз. Тогда , , . Поэтому искомая вероятность по формуле (16) равна .

Источник

Решение задач о бросании игральных костей

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

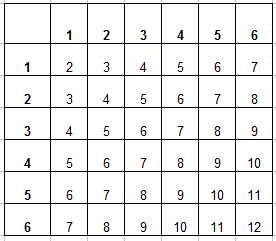
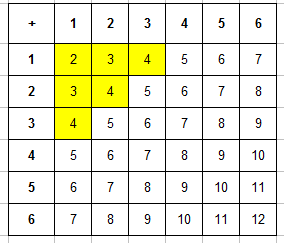
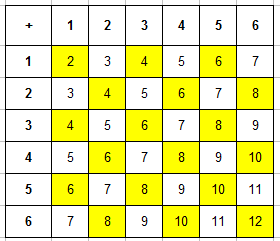
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

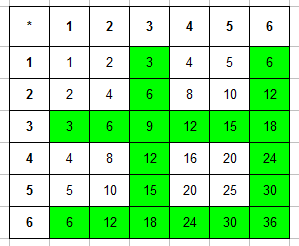
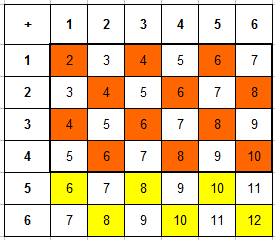
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

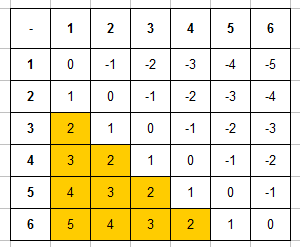
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

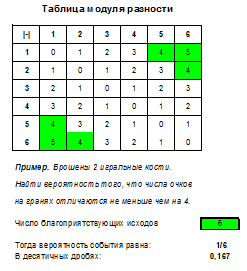
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Теперь подберем такие исходы, которые дают в сумме 15 очков.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Полезные ссылки

Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Источник

Вероятность игральной кости.

Задачи на вероятность игральной кости не менее популярны, чем задачи о подбрасывании монет. Условие такой задачи обычно звучит так: при бросании одной или нескольких игральных костей (2 или 3), какова вероятность того, что сумма очков будет равна 10, или число очков равно 4, или произведение числа очков, или делится на 2 произведение числа очков и так далее.

Применение формулы классической вероятности является основным методом решения задач такого типа.

Одна игральная кость, вероятность.

Задача 1. Один раз брошена игральная кость. Какова вероятность выпадения четного числа очков?

Поскольку игральная кость собой представляет кубик (или его еще называют правильной игральной костью, на все грани кубик выпадет с одинаковой вероятностью, так как он сбалансированный), у кубика 6 граней (число очков от 1 до 6, которые обычно обозначаются точками), это значит, что в задаче общее число исходов: n=6. Событию благоприятствуют только исходы, при которых выпадает грань с четными очками 2,4 и 6, у кубика таких граней: m=3. Теперь можем определить искомую вероятность игральной кости: P=3/6=1/2=0.5.

Задача 2. Брошен один раз игральный кубик. Какова вероятность, что выпадет не менее 5 очков?

Решается такая задача по аналогии с примером, указанным выше. При бросании игрального кубика общее число равновозможных исходов равно: n=6, а удовлетворяют условие задачи (выпало не менее 5 очков, то есть выпало 5 или 6 очков) только 2 исхода, значит m=2. Далее находим нужную вероятность: P=2/6=1/3=0.333.

Две игральные кости, вероятность.

Задача 3. Брошены одновременно 2 игральные кости. Какова вероятность выпадения суммы менее 5 очков?

Теперь можно заполнить таблицу, для этого в каждую ячейку заносится число суммы очков, которые выпали на первой и второй кости. Заполненная таблица выглядит так:

Благодаря таблице определим число исходов, которые благоприятствуют событию » выпадет в сумме менее 5 очков». Произведем подсчет числа ячеек, значение суммы в которых будет меньше числа 5 (это 2, 3 и 4). Такие ячейки для удобства закрашиваем, их будет m=6:

Учитывая данные таблицы, вероятность игральной кости равняется: P=6/36=1/6.

Задача 4. Было брошено две игральные кости. Определить вероятность того, что произведение числа очков будет делиться на 3.

Для решения задачи составим таблицу произведений очков, которые выпали на первой и на второй кости. В ней сразу же выделим числа кратные 3:

Записываем общее число исходов эксперимента n=36 (рассуждения такие же как в предыдущей задаче) и число благоприятствующих исходов (число ячеек, которые закрашены в таблице) m=20. Вероятность события равняется: P=20/36=5/9.

Задача 5. Дважды брошена игральная кость. Какова вероятность, что на первой и второй кости разность числа очков будет равна от 2 до 5?

Чтобы определить вероятность игральной кости запишем таблицу разностей очков и выделим в ней те ячейки, значение разности в которых будет между 2 и 5:

Число благоприятствующих исходов (число ячеек, закрашенных в таблице) равно m=10, общее число равновозможных элементарных исходов будет n=36. Определит вероятность события: P=10/36=5/18.

В случае простого события и при бросании 2-х костей, требуется построить таблицу, затем в ней выделить нужные ячейки и их число поделить на 36, это и будет считаться вероятностью.

Источник

LiveInternetLiveInternet

—Ссылки

—Рубрики

—Метки

—Приложения

—Поиск по дневнику

—Подписка по e-mail

—Статистика

100 готовых задач по теории вероятностей часть 33

3201. Игральную кость подбрасывают 3 раза. Найти вероятность того, что 1) дважды появится число очков, кратное трем; 2) число очков кратное трем появится хотя бы один раз. Готовое решение задачи

3202. Игральная кость подбрасывается 15 раз. Сколько раз в среднем может появиться 4 на верхней грани. Готовое решение задачи

3203. Игральную кость подбрасывают 3 раза. Найти вероятность того, что при этом шестерка:
а) не выпадет ни разу,
б) выпадет по крайней мере два раза. Готовое решение задачи

3204. Какова вероятность, что при пяти подбрасываниях игральной кости шестерка выпадет три раза. Готовое решение задачи

3205. Игральная кость подбрасывается до тех пор, пока не выпадет 3 раза число очков, отличное от 6. Какова вероятность, что «шестерка» выпадет 3 раза. Готовое решение задачи

3206. Игральная кость подбрасывается до тех пор, пока не выпадет 4 раза число очков, отличное от 6. Какова вероятность, что «шестерка» выпадет 2 раза? Готовое решение задачи

3207. Игральная кость подбрасывается до тех пор, пока не выпадет 6 раз число очков, отличное от 5. Какова вероятность, что будет произведено 9 бросков? Готовое решение задачи

3208. Игральная кость подбрасывается до тех пор, пока не выпадет 5 раз число очков, отличное от 6. Какова вероятность, что будет произведено 8 бросков? Готовое решение задачи

3209. Игральная кость подбрасывается восемь раз. Найти вероятность того, что грань с цифрой 5 выпадет ровно 6 раз. Готовое решение задачи

3210. Игральная кость подбрасывается 9 раз. Найдите вероятность того, что а) шестерка выпадет 3 раза; б) шестерка выпадет более 3 раз; в) шестерка выпадет не более семи. Готовое решение задачи

3211. Определить вероятность того, что при пятикратном бросании игральной кости четное число очков выпадает не менее трех раз (следует учесть, что «не менее трех раз» означает 3, 4 или 5 раз (в пяти бросаниях), т.е., рассматривается сумма несовместных событий). Готовое решение задачи

3212. Определить вероятность того, что при пятикратном бросании шестигранной игральной кости четное число очков выпадает не менее двух раз. Готовое решение задачи

3213. Товаровед осматривает 30 образцов товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,7. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже. Готовое решение задачи

3214. Испытание заключается в бросании трёх игральных костей. Найти вероятность того, что в пяти независимых испытаниях ровно два раза выпадет по три единицы. Готовое решение задачи

3215. Испытание состоит в бросании 3 игральных костей. Найдите вероятность того, что в 5 независимых испытаниях ровно 3 раза выпадет по 3 единицы. Готовое решение задачи

3216. Игральная кость подброшена 3 раза. Найдите вероятность того, что четное число очков не выпадет ни разу. Готовое решение задачи

3217. Бросают пять игральных костей. Чему равна вероятность того, что из пяти выпавших цифр одна – четная, а все остальные – нечетные? Готовое решение задачи

3218. Какова вероятность того, что при бросании семи игральных костей шестерка выпадет трижды? Готовое решение задачи

3219. Бросают 5 игральных костей. Найти вероятность того, что на трёх из них выпадет 5. Готовое решение задачи

3220. Игральный кубик подбрасывают три раза. Какова вероятность того, что:
а) шестерка не появится ни разу;
б) шестерка появится хотя бы один раз. Готовое решение задачи

3221. Игральная кость подбрасывается 7 раз. Найти вероятность того, что 6 очков выпадет 4 раза. Готовое решение задачи

3222. Игральную кость подбрасывают 7 раз. Найти вероятность того, что одно очко выпадет не более двух раз. Готовое решение задачи

3223. Найти вероятность того, что при пяти бросаниях игральной кости («пятерка») выпадет не более 2-х раз. Готовое решение задачи

3224. Игральную кость бросают 7 раз. Какова вероятность того, что ни разу не выпадет цифра 6. Готовое решение задачи

3225. Игральная кость подбрасывается семь раз. Найти вероятность того, что грань с цифрой два выпадет ровно четыре раза. Готовое решение задачи

3226. Игральную кость бросают 6 раз. Какова вероятность того, что дважды выпадет число очков, делящееся на три? Готовое решение задачи

3227. Игральную кость бросают 5 раз. Какова вероятность, что тройка выпадет дважды? Готовое решение задачи

3228. Игральную кость бросают 6 раз. Какова вероятность того, что четное число очков выпадет трижды? Готовое решение задачи

3229. Игральную кость бросают 6 раз. Какова вероятность того, что нечетное число очков выпадет в два раза чаще, чем четное. Готовое решение задачи

3230. Игральный кубик подбрасывают 4 раза. Какова вероятность того, что «шестерка» выпадет только один раз? Готовое решение задачи

3231. Игральную кость бросают 4 раза. Какова вероятность того, что цифра 3 выпадет 1 раз? Готовое решение задачи

3232. Игральная кость бросается 4 раза. Найти вероятность следующих событий:
а) «шестерка» выпадет 1 раз.
б) число выпавшей «шестерки» будет в пределах от 2 до 4. Готовое решение задачи

3233. Игральная кость бросается 37 раз. Каково наиболее вероятное количество испытаний, в которых выпадет более 4-x очков? Готовое решение задачи

3234. Чему равна вероятность того, что при 10 бросаниях игральной кости выпадет хотя бы один раз единица? Готовое решение задачи

3235. Игральная кость бросается трижды. Определить вероятность того, что: а) хотя бы один раз выпадет 5 очков; б) три раза выпадет 6 очков; в) два раза выпадет 3 очка. Готовое решение задачи

3236. Найти вероятность того, что при бросании игральной кости три раза не менее 2 раз выпадет 6 очков. Готовое решение задачи

3237. Игральную кость бросают пять раз. Найти вероятность того, что на верхней грани шесть очков при этом выпадет: 1) два раза; 2) более двух раз; 3) менее двух раз. Готовое решение задачи

3238. В урне 6 белых и 5 красных шаров. Случайным образом вынимают 4 шара. Какова вероятность того, что среди них имеется: а) ровно 3 белых шара; б) меньше, чем 3 белых шаров; в) хотя бы 1 белый шар. Готовое решение задачи

3239. В корзине имеется 6 белых и 6 черных шаров. Наудачу извлекается 6 шаров. Какова вероятность того, что это будут 3 белых и 3 черных шара? Готовое решение задачи

3240. В урне содержится 4 черных и 5 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3241. В корзине имеется 8 белых и 5 черных шаров. Наудачу извлекается 6 шаров. Какова вероятность того, что это будут 4 белых и 2 черных шара? Готовое решение задачи

3242. В урне содержится 7 черных и 4 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3243. В корзине имеется 7 белых и 6 черных шаров. Наудачу извлекается 5 шаров. Какова вероятность того, что это будут 2 белых и 3 черных шара? Готовое решение задачи

3244. В урне содержится 6 черных и 7 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 4 белых шара;
б) менее, чем 4 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3245. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 4 белых и 3 черных. Готовое решение задачи

3246. В корзине 9 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3247. В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3248. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 1 черный и 5 красных. Готовое решение задачи

3249. В урне содержится 4 черных и 6 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3250. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 4 черных и 2 красных. Готовое решение задачи

3251. В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3252. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 5 белых и 2 красных. Готовое решение задачи

3253. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 4 белых шара;
б) менее, чем 4 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3254. В корзине 20 белых и 5 чёрных шаров. Наудачу берут 4 шара. Какова вероятность того, что 3 белые и 1 черный? Готовое решение задачи

3255. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3256. В корзине 9 белых, 6 черных и 5 красных шаров. Наудачу извлекают 2 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3257. В урне содержится 6 черных и 5 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3258. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 5 черных и 1 красный. Готовое решение задачи

3259. В корзине 9 белых, 6 чёрных и 3 красных шара. Наудачу извлекают 3 шара. Какова вероятность того, что они разных цветов? Готовое решение задачи

3260. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 5 белых, 1 черный и 1 красный. Готовое решение задачи

3261. В корзине 8 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3262. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 2 черных и 4 красных. Готовое решение задачи

3263. В корзине 9 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что среди них 2 чёрных и 1 красный? Готовое решение задачи

3264. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 2 белых, 1 черный и 4 красных. Готовое решение задачи

3265. В корзине 20 белых и 5 чёрных шаров. Наудачу берут 5 шаров. Какова вероятность того, что 3 белые и 2 чёрный? Готовое решение задачи

3266. Из корзины, в которой находиться 15 белых и 5 черных шаров, вынимают наудачу 2 шара. Какова вероятность того, что оба шара окажутся черными? Готовое решение задачи

3267. Из корзины, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными? Готовое решение задачи

3268. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 2 белых, 4 черных и 1 красный. Готовое решение задачи

3269. В корзине 9 белых и 5 чёрных шаров. Какова вероятность того, что два вынутых шара, различного цвета? Готовое решение задачи

3270. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 4 белых, 1 черный и 2 красных. Готовое решение задачи

3271. В урне из 30 шаров 5 зеленые. Какова вероятность того, что из 7 наугад выбранных шаров один окажется зеленым? Готовое решение задачи

3272. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета. Готовое решение задачи

3273. В урне 3 белых и 7 черных шаров. Из урны вынимают одновременно два шара. Какое событие более вероятно: A – шары одного цвета, B – шары разных цветов? Готовое решение задачи

3274. В урне находится 25 одинаковых по размеру и внешнему виду шаров: среди них 5 белых и 20 черных. Наугад вынимаются 6 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 3 белых? Готовое решение задачи

3275. В урне находится 20 одинаковых по размеру и внешнему виду шаров: среди них 8 белых и 12 черных. Наугад вынимаются 7 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 6 белых? Готовое решение задачи

3276. В урне находится 28 одинаковых по размеру и внешнему виду шаров: среди них 7 белых и 21 черных. Наугад вынимаются 4 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 3 белых? Готовое решение задачи

3277. В урне находится 16 одинаковых по размеру и внешнему виду шаров: среди них 8 белых 8 черных. Наугад вынимаются 8 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 7 белых? Готовое решение задачи

3278. В урне находится 18 одинаковых по размеру и внешнему виду шаров: среди них 9 белых и 9 черных. Наугад вынимаются 7 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 4 белых? Готовое решение задачи

3279. В урне находятся 31 шар одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 8 шаров. Найти вероятность того, что среди вытянутых шаров будет 3 белых. Готовое решение задачи

3280. В урне находятся 13 шаров одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 5 шаров. Найти вероятность того, что среди вытянутых шаров будет 4 белых. Готовое решение задачи

3281. В урне 20 шаров одинакового размера, причем 6 шаров белого цвета, остальные красные. Наудачу вытягивается 7 шаров. Найти вероятность того, что среди вытянутых шаров будет 5 белых. Готовое решение задачи

3282. В урне находятся 31 шар одинакового размера, причем 6 шаров белого цвета, остальные красные. Наудачу вытягивается 8 шаров. Найти вероятность того, что среди вытянутых шаров будет 2 белых. Готовое решение задачи

3283. В урне находятся 23 шара одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 6 шаров. Найти вероятность того, что среди вытянутых шаров будет 1 белый. Готовое решение задачи

3284. В урне находится десять красных, восемь черных и семь белых шаров. Случайно выбирают шесть шаров. Найти вероятность того, что среди них три красных, два черных и один белый. Готовое решение задачи

3285. В урне 5 белых и 10 черных шаров. Чему равна вероятность того, что, вынув наудачу 4 шара, получим белых:
а) не менее 2,
б) ровно 3. Готовое решение задачи

3286. В урне 6 белых, 4 черных и 5 красных шаров. Из урны наугад вынимают 5 шаров. Найти вероятность того, что среди них окажутся 2 белых и 1 черный шар. Готовое решение задачи

3287. Из урны, в которой находятся 8 черных и 4 белых шара, наугад вынимают 2 шара. Найдите вероятность того, что оба шара окажутся белыми. Готовое решение задачи

3288. В урне 6 черных и 4 белых шаров. Из урны извлекают 3 шара. Найти вероятность того, что среди них будет 1 белый. Готовое решение задачи

3289. В урне 6 черных и 4 белых шара. Из урны вынули 3 шара. Найти вероятность того, что среди них будет 2 белых? Готовое решение задачи

3290. В урне находятся 12 шаров, третья часть которых – красные. Наугад взяли 6 шаров. Найти вероятность того, что 4 из них будут красные. Готовое решение задачи

3291. В урне 5 белых, 6 черных и 9 красных шаров. Из урны наугад извлекаются 3 шара. Какова вероятность того, что все они – разных цветов. Готовое решение задачи

3292. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Готовое решение задачи

3293. В урне 12 белых, 5 красных и 3 черных шара. Наудачу вынимается три шара. Найдите вероятность того, что
а) все шары будут красными?
б) хотя бы один шар будет черным?
в) два шара будут белыми? Готовое решение задачи

3294. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара? Готовое решение задачи

3295. В урне 40 шаров: 15 белых, 15 красных и 10 синих. Найти вероятность появления цветного шара. Готовое решение задачи

3296. В урне находятся 4 черных, 7 красных, 9 зеленых и 11 синих шаров. Оттуда вынули один шар. Найти вероятность появления цветного шара (не черного). Готовое решение задачи

3297. В ящике 20 шаров: 5 белых, 5 синих и 10 красных. Найти вероятность появления цветного шара. Готовое решение задачи

3298. В урне содержится 13 зеленых, 10 желтых, 8 белых шаров. Найдите вероятность появления цветного шара. Готовое решение задачи

3299. В урне 100 шаров, из них 5 белые, остальные – черные. Какова вероятность того, что из 4-х наугад выбранных шаров два окажутся белыми? Готовое решение задачи

3300. В урне 10 шаров, из них 4 белые, остальные – чёрные. Какова вероятность того, что из 3-х наугад выбранных шаров два окажутся белыми? Готовое решение задачи

Источник