Коэффициент что это значит

КОЭФФИЦИЕНТ

Смотреть что такое «КОЭФФИЦИЕНТ» в других словарях:

КОЭФФИЦИЕНТ — в алгебре: постоянная величина, показывающая, сколько раз взято слагаемым стоящее рядом с нею выражение; в физике: число, которым измеряется сила к. н. явления, нпр., упругости. Полный словарь иностранных слов, вошедших в употребление в русском… … Словарь иностранных слов русского языка

КОЭФФИЦИЕНТ — в статистике показатель, выраженный относительными величинами. Отражает: скорость развития какого либо явления (т. н. коэффициент динамики), частоту возникновения явления (напр., коэффициент рождаемости), взаимосвязь качественно различных явлений … Большой Энциклопедический словарь

КОЭФФИЦИЕНТ — КОЭФФИЦИЕНТ, число, на которое умножается некоторая неизвестная величина в алгебраическом выражении. В выражении 1 + 5х + 2х2 числа 5 и 2 являются коэффициентами х и х2 соответственно. В физике коэффициент это число, характеризующее определенное… … Научно-технический энциклопедический словарь

коэффициент — компонента, составляющая, член, множитель, фактор, отношение, пропорция, соотношение, степень, процент, показатель, индекс, параметр, характеристика; кпд Словарь русских синонимов. коэффициент сущ., кол во синонимов: 9 • брутто коэффици … Словарь синонимов

коэффициент — а, м. coefficient <, н. лат. coefficiens, ntis. 1. Мат. Множитель (числовой или буквенный) в алгебраическом выражении. Сл. 18. Надлежит же неоставить учинять делать примечании юношам при умножении алгебраическом возышение степеней. Как члены… … Исторический словарь галлицизмов русского языка

КОЭФФИЦИЕНТ — (от лат. co совместно и efficiens производящий) множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч … Большой Энциклопедический словарь

коэффициент J — коэффициент креновой девиации Изменение в девиации компаса на каждый градус крена судна на правый борт, если судно идет по компасу курсом на север. [ГОСТ Р 52682 2006] Тематики средства навигации, наблюдения, управления Синонимы коэффициент… … Справочник технического переводчика

КОЭФФИЦИЕНТ — (от латинского co совместно и efficiens производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициент при них называют также произведение всех постоянных, в … Современная энциклопедия

КОЭФФИЦИЕНТ — (coefficient) Числа или алгебраические выражения, определяющие структуру математического выражения или уравнения. Например, в уравнении y = ax2+bx+c, a является коэффициентом x2, b – коэффициентом х, а с – постоянным членом. Экономика. Толковый… … Экономический словарь

КОЭФФИЦИЕНТ — см. Коэффициент эффективности промышленных открытий. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Источник

КОЭФФИЦИЕНТ

Смотреть что такое «КОЭФФИЦИЕНТ» в других словарях:

КОЭФФИЦИЕНТ — в алгебре: постоянная величина, показывающая, сколько раз взято слагаемым стоящее рядом с нею выражение; в физике: число, которым измеряется сила к. н. явления, нпр., упругости. Полный словарь иностранных слов, вошедших в употребление в русском… … Словарь иностранных слов русского языка

КОЭФФИЦИЕНТ — в статистике показатель, выраженный относительными величинами. Отражает: скорость развития какого либо явления (т. н. коэффициент динамики), частоту возникновения явления (напр., коэффициент рождаемости), взаимосвязь качественно различных явлений … Большой Энциклопедический словарь

КОЭФФИЦИЕНТ — КОЭФФИЦИЕНТ, число, на которое умножается некоторая неизвестная величина в алгебраическом выражении. В выражении 1 + 5х + 2х2 числа 5 и 2 являются коэффициентами х и х2 соответственно. В физике коэффициент это число, характеризующее определенное… … Научно-технический энциклопедический словарь

коэффициент — компонента, составляющая, член, множитель, фактор, отношение, пропорция, соотношение, степень, процент, показатель, индекс, параметр, характеристика; кпд Словарь русских синонимов. коэффициент сущ., кол во синонимов: 9 • брутто коэффици … Словарь синонимов

коэффициент — а, м. coefficient <, н. лат. coefficiens, ntis. 1. Мат. Множитель (числовой или буквенный) в алгебраическом выражении. Сл. 18. Надлежит же неоставить учинять делать примечании юношам при умножении алгебраическом возышение степеней. Как члены… … Исторический словарь галлицизмов русского языка

КОЭФФИЦИЕНТ — (от лат. co совместно и efficiens производящий) множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч … Большой Энциклопедический словарь

коэффициент J — коэффициент креновой девиации Изменение в девиации компаса на каждый градус крена судна на правый борт, если судно идет по компасу курсом на север. [ГОСТ Р 52682 2006] Тематики средства навигации, наблюдения, управления Синонимы коэффициент… … Справочник технического переводчика

КОЭФФИЦИЕНТ — (от латинского co совместно и efficiens производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициент при них называют также произведение всех постоянных, в … Современная энциклопедия

КОЭФФИЦИЕНТ — см. Коэффициент эффективности промышленных открытий. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Источник

Коэффициент – что означает? Определение, значение, примеры употребления

Ищешь, что значит слово коэффициент? Пытаешься разобраться, что такое коэффициент? Вот ответ на твой вопрос:

Значение слова «коэффициент» в словарях русского языка

Коэффициент это:

Коэффицие́нт (от «совместно» + «производящий») — числовой множитель при буквенном выражении, множитель при той или иной степени неизвестного, или постоянный множитель при переменной величине.

Коэффициент

м.
1. Числовой или буквенный множитель в алгебраическом выражении.
2. величина, определяющая какое-либо свойство физического тела.
3. число, на которое нужно умножить какую-либо величину, чтобы получить требуемую при данных условиях.

Коэффициент

(лат. coefficiens (coelfi-cientis) содействующий) мат. обычно постоянная или известная величина, являющаяся множителем при другой, обычно переменной или неизвестной величине; к. пропорциональности — постоянное число, которое, будучи помножено на любое значение одной величины, дает произведение, равное соответствующему значению другой величины, пропорциональной первой; к. полезного действия — величина, показывающая, какая часть затрачиваемой энергии превращается в полезную работу; обычно выражается в процентах.

Коэффициент

м.
1) а) Числовой или буквенный множитель в алгебраическом выражении. б) Число, на которое нужно помножить какую-л. величину, чтобы получить требуемую при данных условиях.
2) Величина, определяющая какое-л. свойство физического тела.

Коэффициент

Коэффициент

[мат. обычно постоянная или известная величина, являющаяся множителем при другой, обычно переменной или неизвестной величине; к. пропорциональности — постоянное число, которое, будучи помножено на любое значение одной величины, дает произведение, равное соответствующему значению другой величины, пропорциональной первой; к. полезного действия — величина, показывающая, какая часть затрачиваемой энергии превращается в полезную работу; обычно выражается в процентах.

Коэффициент

Коэффициент

числовой или буквенный множитель в алгебрическом выражении коэффициент относительная величина, определяющая свойство какого-н, процесса или устройства К. трения. К. полезного действия (отношение количества полезной работы механизма, системы к количеству поглощаемой им энергии; спец.). К. трудового участия (в рабочих коллективах: относительная доля трудового вклада каждого работающего). Поправочный к. (устанавливаемый при поправках каких-н. величин; спец.).

Коэффициент

в статистике — показатель, выраженный относительными величинами. Отражает: скорость развития какого-либо явления (т. н. коэффициент динамики), частоту возникновения явления (напр., коэффициент рождаемости), взаимосвязь качественно различных явлений (напр., коэффициент плотности населения), степень использования материальных, трудовых или денежных ресурсов (напр., коэффициент эффективности), вариацию величин признака (напр., коэффициент ритмичности). — (от лат. co — совместно и efficiens — производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч. и выраженных буквами. Многие коэффициенты в физических законах имеют особые названия, напр. коэффициент трения, коэффициент поглощения света.

Коэффициент

коэффициент м.
1) а) Числовой или буквенный множитель в алгебраическом выражении. б) Число, на которое нужно помножить какую-л. величину, чтобы получить требуемую при данных условиях.
2) Величина, определяющая какое-л. свойство физического тела.

Коэффициент

соотношение двух величин, имеющих одинаковые единицы измерения. К. характеризует относительное изменение какого-либо одного признака.

Коэффициент

АБСЕНТЕИЗМА — отношение числа дней невыхода на работу к общему числу рабочих дней в течение месяца, года.

Коэффициент

Коэффициент

Коэффициент

ВОССТАНОВЛЕНИЯ (УТРАТЫ) ПЛАТЕЖЕСПОСОБНОСТИ — коэффициент, характеризующий наличие у предприятия реальной возможности восстановить либо утратить свою платежеспособность в течение определенного времени. Рассчитывается как отношение расчетного коэффициента текущей ликвидности к его установленному значению. Расчетный коэффициент текущей ликвидности определяется как сумма фактического значения коэффициента текущей ликвидности на конец отчетного периода и изменения значения этого коэффициента между окончанием и началом отчетного периода в пересчете на установленный период восстановления (утраты) платежеспособности.

Коэффициент

ВЫРУЧКИ — отношение разности между выручкой и переменными расходами к величине выручки.

Коэффициент

ДЕЛЬТА — отношение цены опциона к цене финансового инструмента, на который получен опцион.

Коэффициент

ДЖИНИ — коэффициент, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютного равного их распределения между всеми жителями страны. См. тж. ИНДЕКС КОНЦЕНТРАЦИИ ДОХОДОВ.

Коэффициент

ЗАДОЛЖЕННОСТИ — показатель финансовой деятельности предприятия равный отношению денежных обязательств предприятия (задолженности, заемного капитала) к ее собственному капиталу.

Коэффициент

КУКА — коэффициент платежеспособности кредитных учреждений и коммерческих банков, равный отношению собственного капитала к активам, взвешенным по степени риска.

Коэффициент

ЛИКВИДНОСТИ — коэффициент, характеризующий платежеспособность фирмы, отношение оборотных средств к краткосрочным обязательствам.

Коэффициент

Коэффициент

РЕЗЕРВИРОВАНИЯ. отношение суммы резервных средств к объему оборотного капитала.

Коэффициент

Коэффициент

РИТМИЧНОСТИ — отношение минимальных выпусков продукции к средним.

Коэффициент

СМЕННОСТИ — отношение числа человеко-дней, отработанных во всех сменах, к числу человеко-дней, отработанных в первой смене.

Коэффициент

СООТНОШЕНИЯ ПОКРЫТИЯ — коэффициент, показывающий, во сколько раз доходы компании превосходят сумму дивидендов.

Коэффициент

Коэффициент

Коэффициент

ТРУДОВОГО УЧАСТИЯ — коэффициент, отражающий количественную оценку меры трудового участия отдельного работника в общих результатах труда группы работников.

Коэффициент

ТРУДОЕМКОСТИ — коэффициент, отражающий затраты труда в расчете на единицу произведенной продукции.

Коэффициент

ФЕРТИЛЬНОСТИ — коэффициент, выражающий отношение числа рождений к численности женщин репродуктивного возраста

Коэффициент

ХЕДЖИРОВАНИЯ — см КОЭФФИЦИЕНТ «ДЕЛЬТА».

Коэффициент

ЭЛАСТИЧНОСТИ — показатель, характеризующий меру чувствительности экономической величины по отношению к факторам, от которых она зависит. Измеряется изменением количества экономической величины (например, величины спроса, предложения) при изменении фактора (например, цены) на единицу В математическом смысле Н.э. есть производная от экономической величины по фактору, от которого зависит данная величина.

Коэффициент

ЭФФЕКТИВНОСТИ — отношение результата к обусловившим его затратам. Результат и затраты могут быть выражены как в однородных, так и в неоднородных измерителях.

Коэффициент

МАРЖИНАЛЬНОГО ДОХОДА — отношение маржинального дохода предприятия к объему чистых продаж за тот же период времени.

Коэффициент

НАЛИЧНОСТИ — отношение суммы наличности и аналогичных активов к сумме обязательств.

Коэффициент

Коэффициент

ОБСЛУЖИВАНИЯ ВНЕШНЕГО ДОЛГА — показатель, характеризующий издержки, которые несет государство в связи с обслуживанием внешней задолженности, в т.ч. задолженности частных предпринимателей и долга, гарантированного государством. Издержки, включающие выплату процентов и погашение основной суммы долга, соотносятся с экспортными поступлениями. Точно определить максимальную допустимость задолженности достаточно трудно, однако считается, что 20 % валютной выручки от экспорта является предельной величиной.

Коэффициент

ОТНОСИТЕЛЬНОЙ ДОХОДНОСТИ — отношение прибыли, полученной компанией за последний год, в расчете на сто акций, к текущей их цене.

Коэффициент

ОХВАТА — доля производства товара корпорациями, группами предприятий в общем объеме производства в стране.

Коэффициент

ПОКРЫТИЯ ДОЛГОСРОЧНОЙ ЗАДОЛЖЕННОСТИ — отношение долгосрочной задолженности к совокупным активам или акционерному капиталу предприятия.

Коэффициент

ПРИБЫЛЬНОСТИ — отношение чистого дохода (прибыли) предприятия к объему реализации (выручке от продаж) или капиталу предприятия.

Коэффициент

Коэффициент

[от лат. со (cum) — совместно и efficiens — производящий], числовой множитель при буквенном выражении, известный множитель при той или иной степени неизвестного или постоянный множитель при переменной величине. Так, в одночлене a2b3 К. есть ; в уравнении x2 + 2 px + q 0 К. при x2 есть 1, а К. при х равен 2p; формуле длины окружности l 2p r К. есть 2p. В уравнении прямой у кх + b число k, выражающее тангенс угла наклона прямой к оси Ox, называется угловым К. Многие К. в формулах, выражающих физические законы, имеют особые названия, например К. трения, К. поглощения света и др.

Коэффициент

Коэффициент

показатель, фактор, параметр, представляющий отношение двух однородно исчисленных величин числовой множитель в функциональной зависимости

Где и как употребляется слово «коэффициент»?

Кроме значения слова «коэффициент» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «коэффициент».

Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «коэффициент» в тексте и устной речи.

Примеры употребления слова «коэффициент»

Часть 3 нацелена на быстрое повышение коэффициента интеллекта – IQ.

На сегодняшний день такие элементы обладают пока примерно в четыре раза более низким коэффициентом полезного действия, чем традиционные батареи на основе кремния, но они значительно проще и дешевле в производстве.

Люди с высоким коэффициентом умственного развития часто плохо работали, а те, чьи показатели были весьма скромны, проявляли себя в работе просто отлично.

Источник

коэффициент

Коэффициент прочности. | Это человек с чрезвычайно высоким коэффициентом интеллекта.

Полярный коэффициент зарплаты. | Высчитать коффициент производительности труда.

Смотреть что такое «коэффициент» в других словарях:

КОЭФФИЦИЕНТ — в алгебре: постоянная величина, показывающая, сколько раз взято слагаемым стоящее рядом с нею выражение; в физике: число, которым измеряется сила к. н. явления, нпр., упругости. Полный словарь иностранных слов, вошедших в употребление в русском… … Словарь иностранных слов русского языка

КОЭФФИЦИЕНТ — в статистике показатель, выраженный относительными величинами. Отражает: скорость развития какого либо явления (т. н. коэффициент динамики), частоту возникновения явления (напр., коэффициент рождаемости), взаимосвязь качественно различных явлений … Большой Энциклопедический словарь

КОЭФФИЦИЕНТ — КОЭФФИЦИЕНТ, число, на которое умножается некоторая неизвестная величина в алгебраическом выражении. В выражении 1 + 5х + 2х2 числа 5 и 2 являются коэффициентами х и х2 соответственно. В физике коэффициент это число, характеризующее определенное… … Научно-технический энциклопедический словарь

коэффициент — компонента, составляющая, член, множитель, фактор, отношение, пропорция, соотношение, степень, процент, показатель, индекс, параметр, характеристика; кпд Словарь русских синонимов. коэффициент сущ., кол во синонимов: 9 • брутто коэффици … Словарь синонимов

коэффициент — а, м. coefficient <, н. лат. coefficiens, ntis. 1. Мат. Множитель (числовой или буквенный) в алгебраическом выражении. Сл. 18. Надлежит же неоставить учинять делать примечании юношам при умножении алгебраическом возышение степеней. Как члены… … Исторический словарь галлицизмов русского языка

КОЭФФИЦИЕНТ — (от лат. co совместно и efficiens производящий) множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч … Большой Энциклопедический словарь

коэффициент J — коэффициент креновой девиации Изменение в девиации компаса на каждый градус крена судна на правый борт, если судно идет по компасу курсом на север. [ГОСТ Р 52682 2006] Тематики средства навигации, наблюдения, управления Синонимы коэффициент… … Справочник технического переводчика

КОЭФФИЦИЕНТ — (от латинского co совместно и efficiens производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициент при них называют также произведение всех постоянных, в … Современная энциклопедия

КОЭФФИЦИЕНТ — (coefficient) Числа или алгебраические выражения, определяющие структуру математического выражения или уравнения. Например, в уравнении y = ax2+bx+c, a является коэффициентом x2, b – коэффициентом х, а с – постоянным членом. Экономика. Толковый… … Экономический словарь

КОЭФФИЦИЕНТ — см. Коэффициент эффективности промышленных открытий. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Источник

КОЭФФИЦИЕНТ

— числовой множитель при буквенном выражении, известный множитель при той или иной степени неизвестного или постоянный множитель при переменной величине. Так, в одночлене К. есть в уравнении К. при х 2 есть 1, а К. при хравен 2р; в формуле длины окружности l=2pr К. есть 2p. В уравнении прямой y=kx+b число k, выражающее тангенс угла наклона прямой к оси Ох, наз. угловым коэффициентом. БСЭ-З.

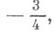
Смотреть что такое «КОЭФФИЦИЕНТ» в других словарях:

КОЭФФИЦИЕНТ — в алгебре: постоянная величина, показывающая, сколько раз взято слагаемым стоящее рядом с нею выражение; в физике: число, которым измеряется сила к. н. явления, нпр., упругости. Полный словарь иностранных слов, вошедших в употребление в русском… … Словарь иностранных слов русского языка

КОЭФФИЦИЕНТ — в статистике показатель, выраженный относительными величинами. Отражает: скорость развития какого либо явления (т. н. коэффициент динамики), частоту возникновения явления (напр., коэффициент рождаемости), взаимосвязь качественно различных явлений … Большой Энциклопедический словарь

КОЭФФИЦИЕНТ — КОЭФФИЦИЕНТ, число, на которое умножается некоторая неизвестная величина в алгебраическом выражении. В выражении 1 + 5х + 2х2 числа 5 и 2 являются коэффициентами х и х2 соответственно. В физике коэффициент это число, характеризующее определенное… … Научно-технический энциклопедический словарь

коэффициент — компонента, составляющая, член, множитель, фактор, отношение, пропорция, соотношение, степень, процент, показатель, индекс, параметр, характеристика; кпд Словарь русских синонимов. коэффициент сущ., кол во синонимов: 9 • брутто коэффици … Словарь синонимов

коэффициент — а, м. coefficient <, н. лат. coefficiens, ntis. 1. Мат. Множитель (числовой или буквенный) в алгебраическом выражении. Сл. 18. Надлежит же неоставить учинять делать примечании юношам при умножении алгебраическом возышение степеней. Как члены… … Исторический словарь галлицизмов русского языка

КОЭФФИЦИЕНТ — (от лат. co совместно и efficiens производящий) множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициентом при них называют также произведение всех постоянных, в т. ч … Большой Энциклопедический словарь

коэффициент J — коэффициент креновой девиации Изменение в девиации компаса на каждый градус крена судна на правый борт, если судно идет по компасу курсом на север. [ГОСТ Р 52682 2006] Тематики средства навигации, наблюдения, управления Синонимы коэффициент… … Справочник технического переводчика

КОЭФФИЦИЕНТ — (от латинского co совместно и efficiens производящий), множитель, обычно выражаемый цифрами. Если произведение содержит одну или несколько переменных (или неизвестных) величин, то коэффициент при них называют также произведение всех постоянных, в … Современная энциклопедия

КОЭФФИЦИЕНТ — (coefficient) Числа или алгебраические выражения, определяющие структуру математического выражения или уравнения. Например, в уравнении y = ax2+bx+c, a является коэффициентом x2, b – коэффициентом х, а с – постоянным членом. Экономика. Толковый… … Экономический словарь

КОЭФФИЦИЕНТ — см. Коэффициент эффективности промышленных открытий. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Источник