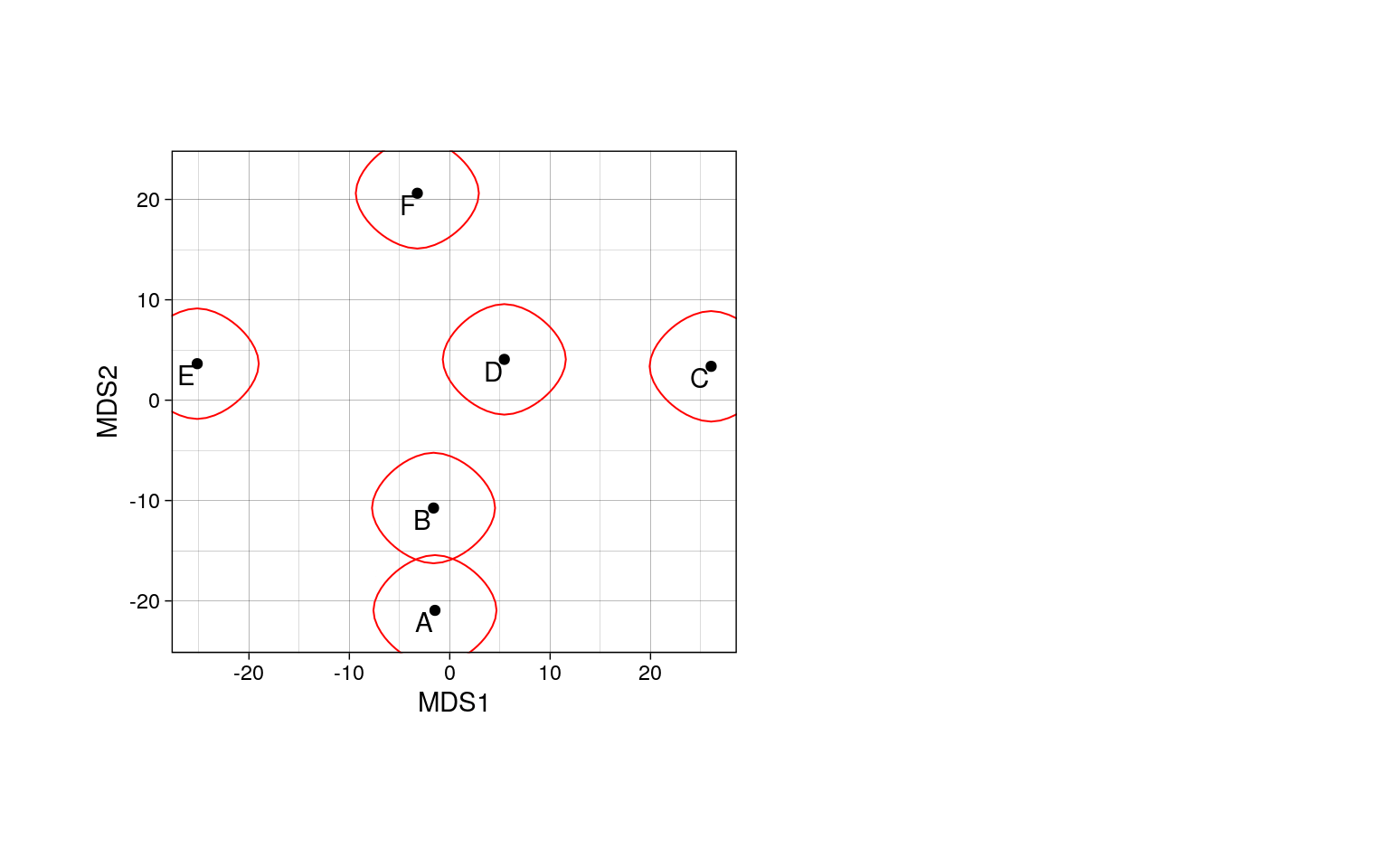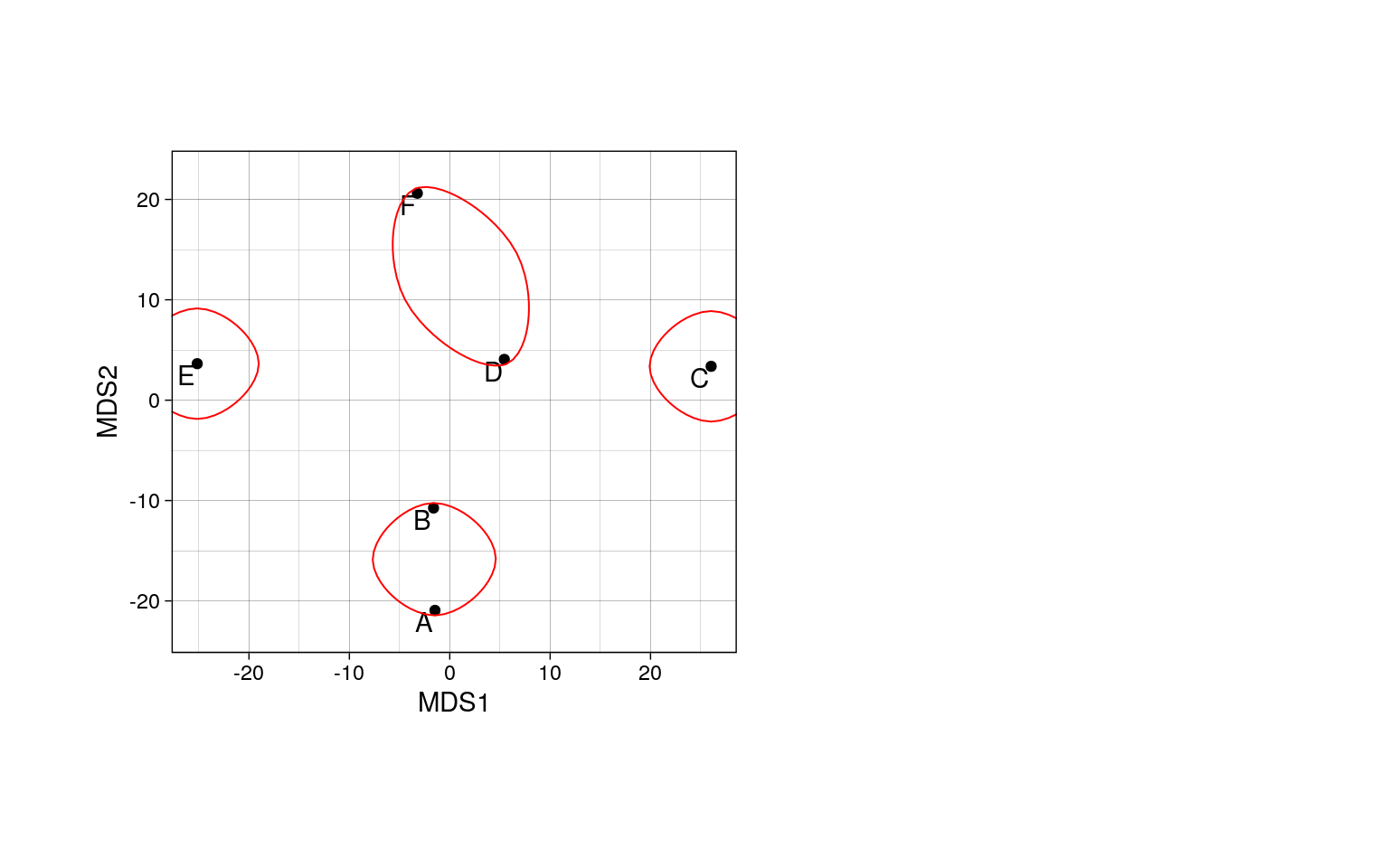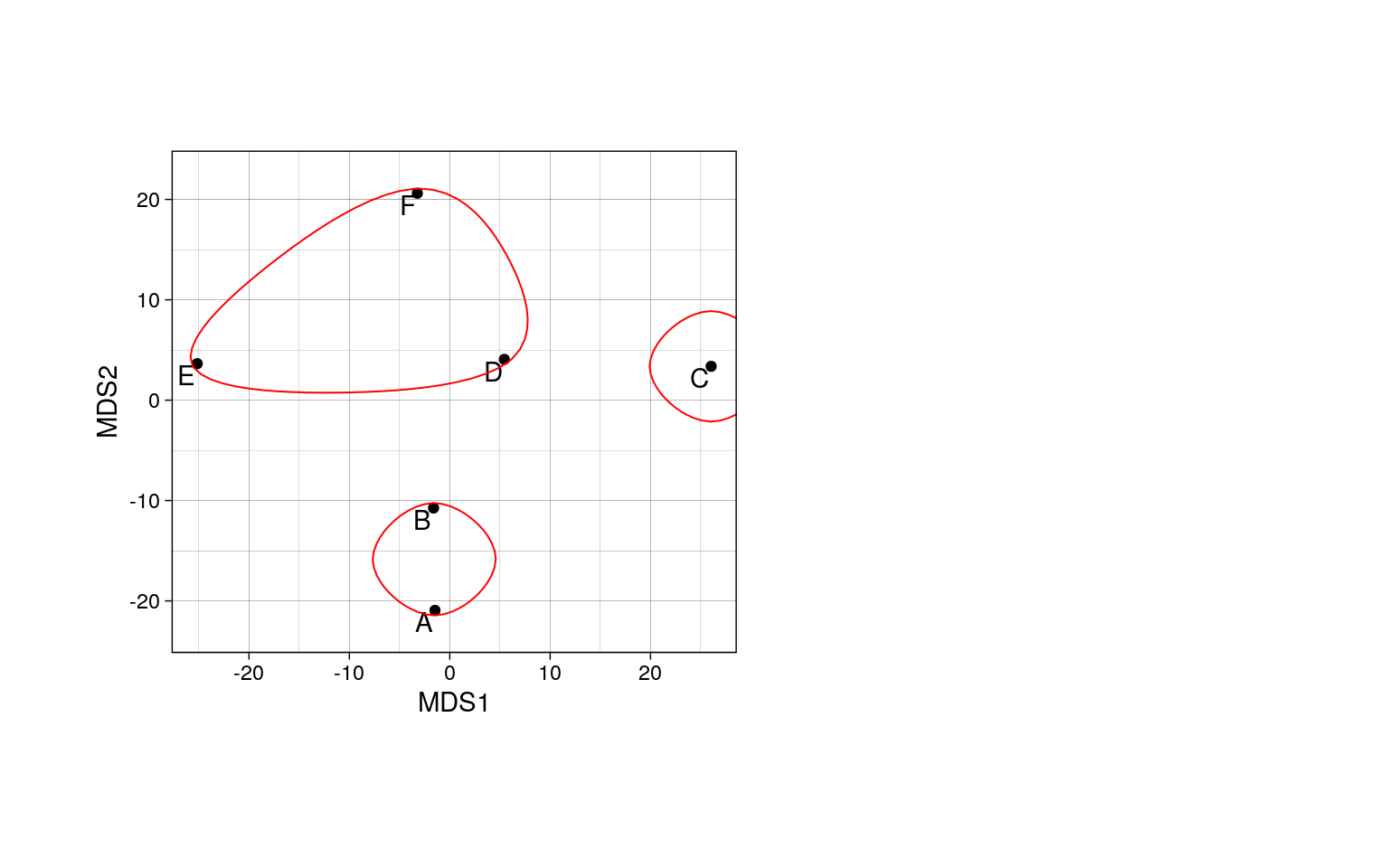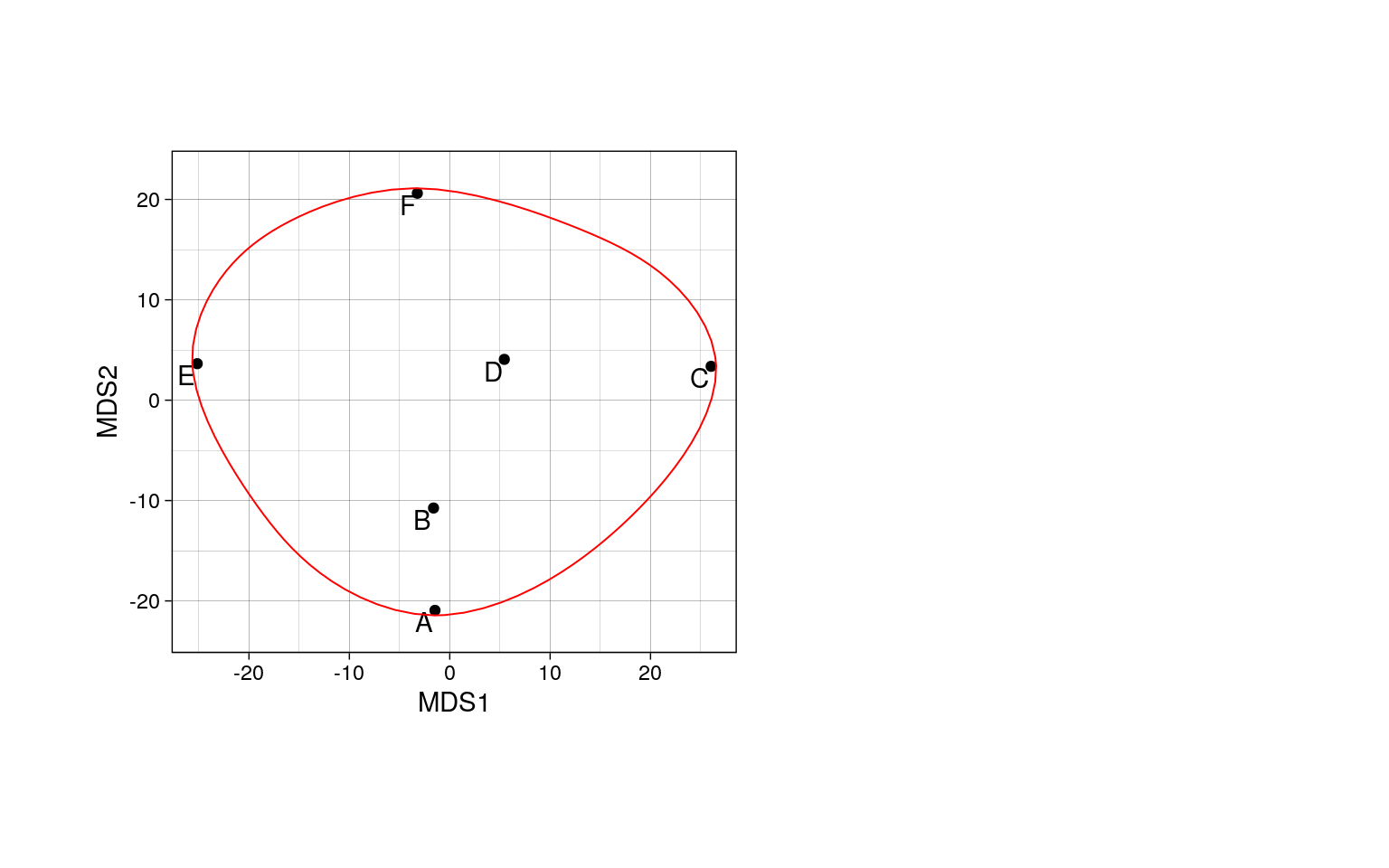
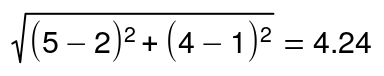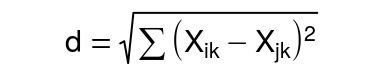Коэффициент жаккара показывает что
Классификация и ординация
Марина Варфоломеева
Данные о протеоме жабр гребешка Pecten maximus от авторов пакета prot2D (Artigaud et al. 2013) :
Данные о протеоме сыворотки крови пациентов, страдающих разной степенью гиперплазии предстательной железы, из пакета digeR (Fan et al. 2009) :
Пакеты (инсталлируйте при необходимости)
Многомерные данные
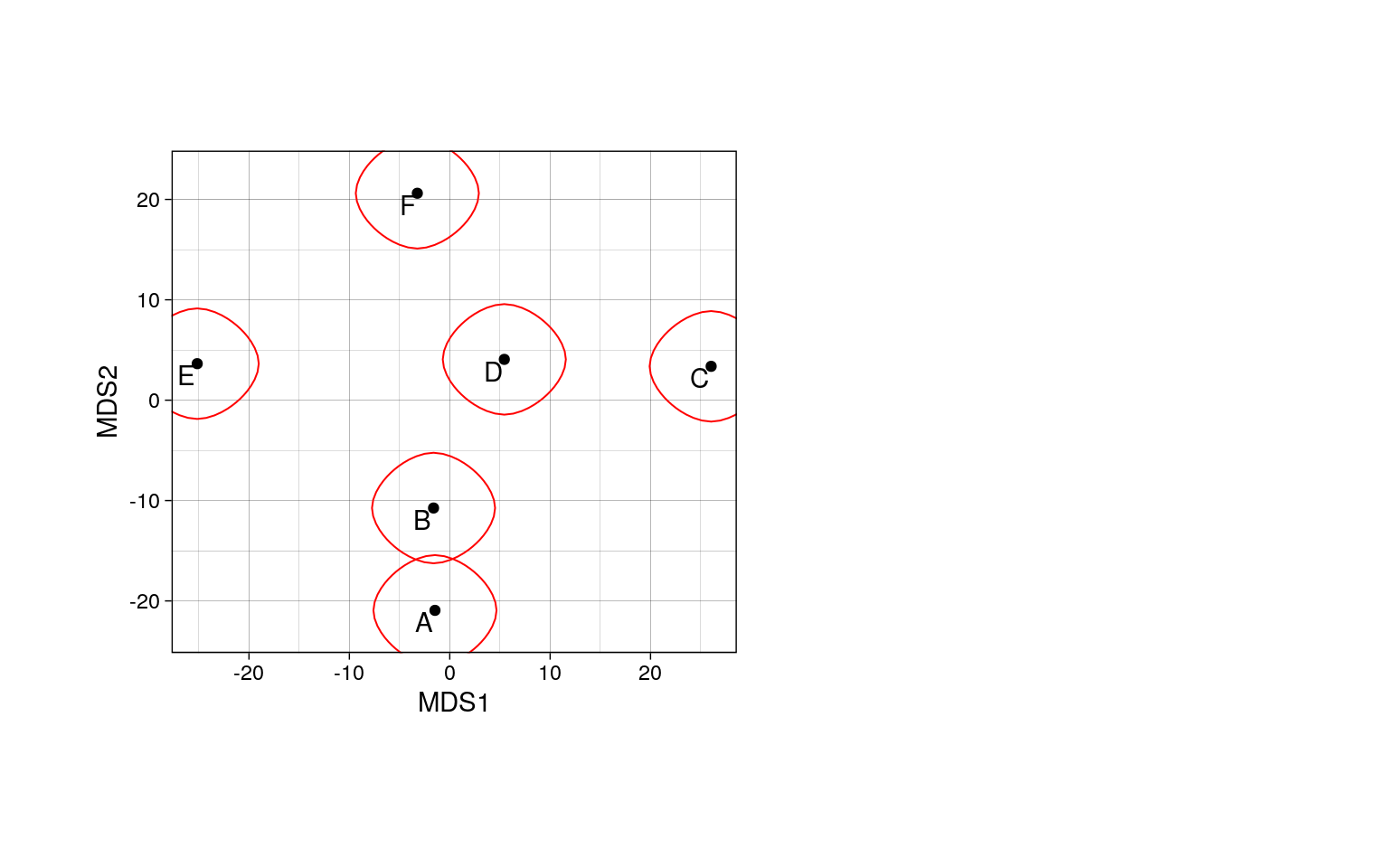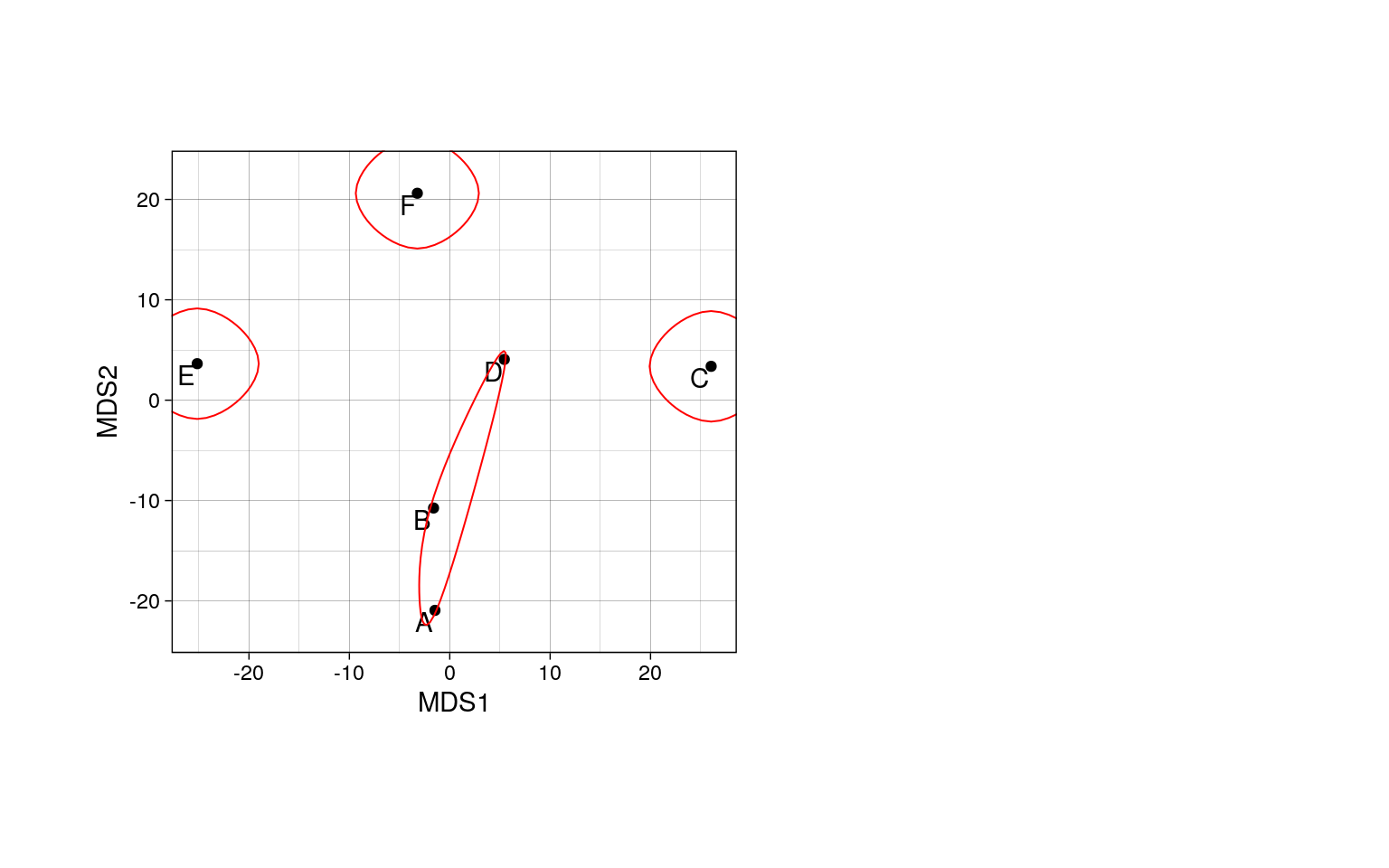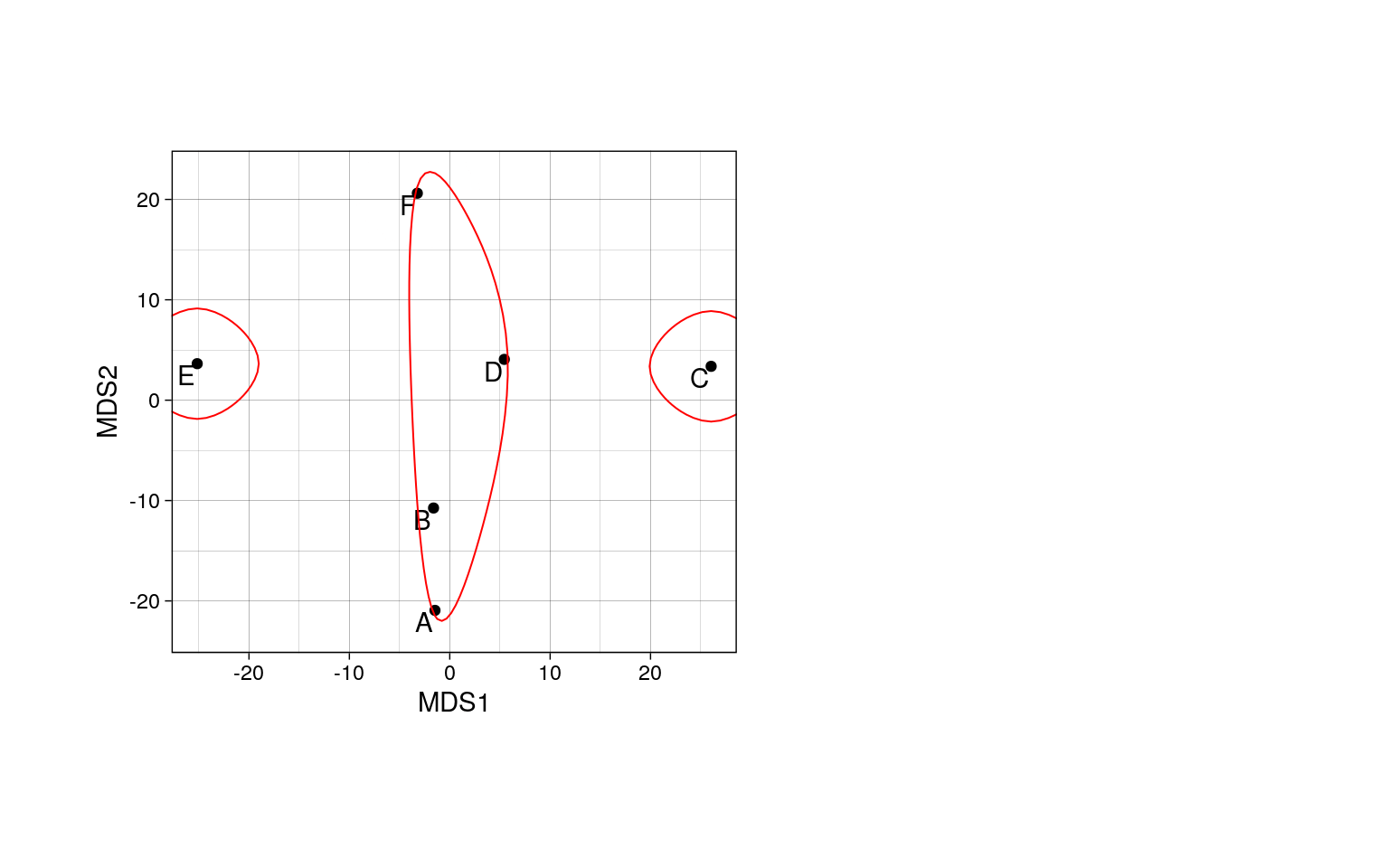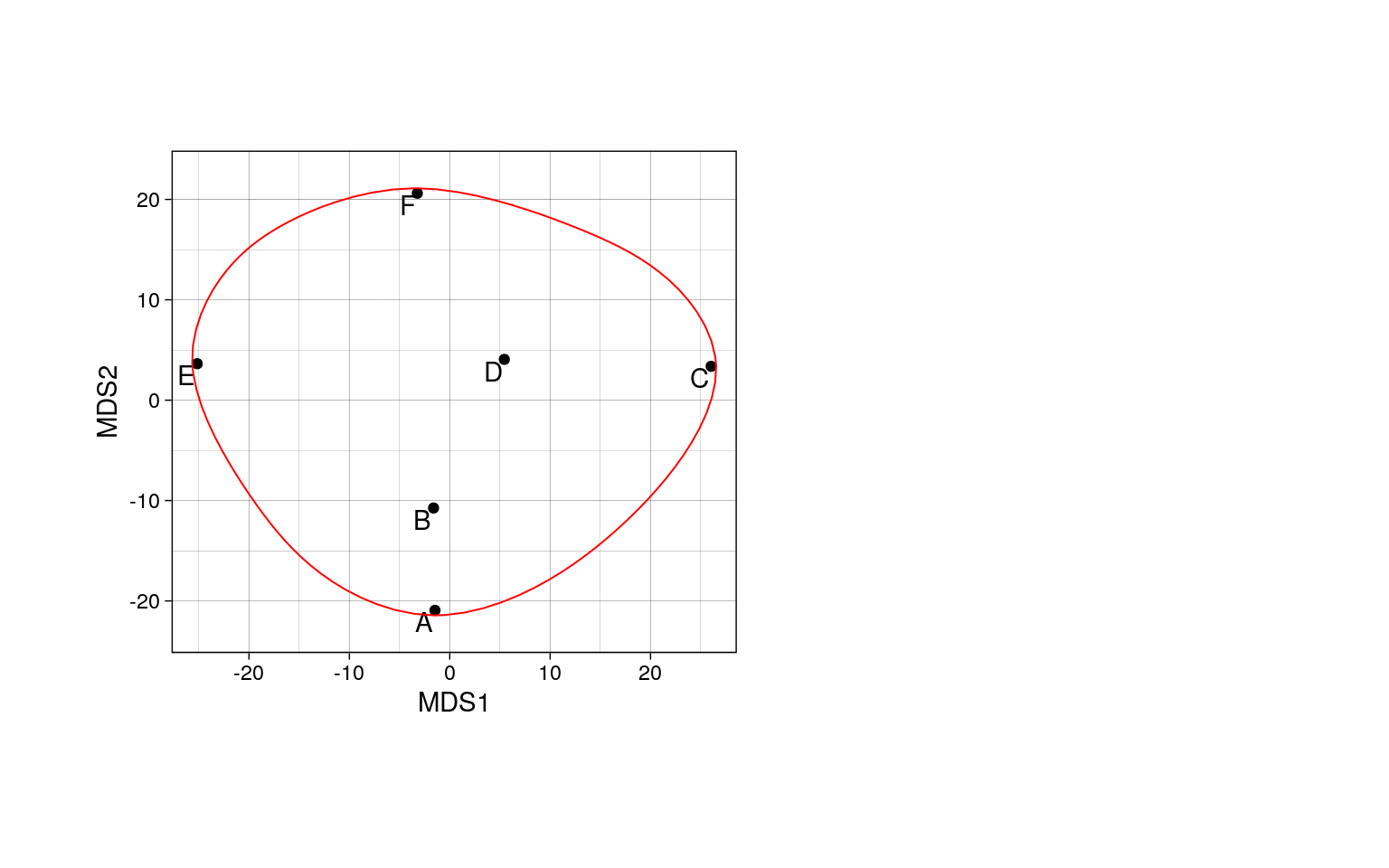
Облако точек в многомерном пространстве
Когда признаков много, можно представить все объекты как облако точек в многомерном пространстве.
Migration by Don McCullough on Flickr
Для изображения N объектов в идеале нужно N-1 измерений
Многомерное пространство сложно изобразить. Есть два пути:
black shadows for a white horses / les negres ombres dels cavalls blancs by Ferran Jordà on Flickr
Коэффициенты сходства-различия
\(0 \le S \le 1\) или \(-1 \le S \le 1\)
Евклидово расстояние
Для двумерного пространства Евклидово расстояние рассчитывается так:
Т.е. Евклидово расстояние в этом гипотетическом примере будет
Для пространства с большим числом измерений формула Евклидова расстояния выглядит так:
Евклидово расстояние — это метрика.
Для всех метрик (расстояний) справедливы три свойства:
Триангулярность есть только у метрик! Именно потому, что для них выполняется неравенство треугольника, они имеют право называться расстояниями, а не просто мерами различия.
Коэффициент Жаккара
Если используются бинарные данные, то посчитать сходство можно, учитывая присутствие-отсутствие признаков.
Коэффициентов сходства-различия для качественных данных придумано великое множество.
Коэффициент Жаккара рассчитывается по формуле:
Соответствующий коэффициент различия Жаккара можно посчитать так:
У коэффициента Жаккара есть одно забавное свойство. Обратите внимание, в знаменателе фигурирует не общее число признаков — сходство по отсутствию не учитывается! Это свойство очень полезно для работы с протеомными данными. Пятно может отсутствовать на геле не только потому, что белка не было в пробе, но и в силу самых разных других причин (например, экспрессия ниже порога определения, плохо прокрашен образец и проч.).
Например, пусть у нас есть три пробы, у которых мы нашли всего 5 пятен.
| Objects | Spot.1 | Spot.2 | Spot.3 | Spot.4 | Spot.5 |
|---|---|---|---|---|---|
| Object 1 | 1 | 1 | 0 | 1 | 0 |
| Object 2 | 1 | 1 | 1 | 1 | 0 |
| Object 3 | 0 | 0 | 0 | 1 | 0 |
Чтобы оценить различие между этими пробами, можно посчитать коэффициент Жаккара.
| Object 1 | Object 2 | Object 3 | |
|---|---|---|---|
| Object 1 | 0.00 | 0.25 | 0.67 |
| Object 2 | 0.25 | 0.00 | 0.75 |
| Object 3 | 0.67 | 0.75 | 0.00 |
Точно так же, чтобы оценить различие белков, можно посчитать коэффициент Жаккара между белками.
| Spot 1 | Spot 2 | Spot 3 | Spot 4 | Spot 5 | |
|---|---|---|---|---|---|
| Spot 1 | 0.00 | 0.00 | 0.50 | 0.33 | 1 |
| Spot 2 | 0.00 | 0.00 | 0.50 | 0.33 | 1 |
| Spot 3 | 0.50 | 0.50 | 0.00 | 0.67 | 1 |
| Spot 4 | 0.33 | 0.33 | 0.67 | 0.00 | 1 |
| Spot 5 | 1.00 | 1.00 | 1.00 | 1.00 | 0 |
Визуализация многомерных данных
Иерархическая кластеризация
Существует много методов классификации: методы кластеризации на основании расстояний и методы кластеризации на основании признаков.
В этом курсе мы будем затрагивать только методы иерархической кластеризации на основании расстояний.
Классификация данных проходит в несколько этапов. Результат кластеризации будет сильнее всего зависеть (1) от выбора коэффициента сходства-различия и (2) от алгоритма кластеризации. Нет формальных способов выбрать наиболее подходящий коэффициент и алгоритм.
Алгоритмы иерархической кластеризации на основании расстояний
Мы рассмотрим несколько алгоритмов, которые строят иерархическую кластеризацию объектов на основании матрицы различий между ними:
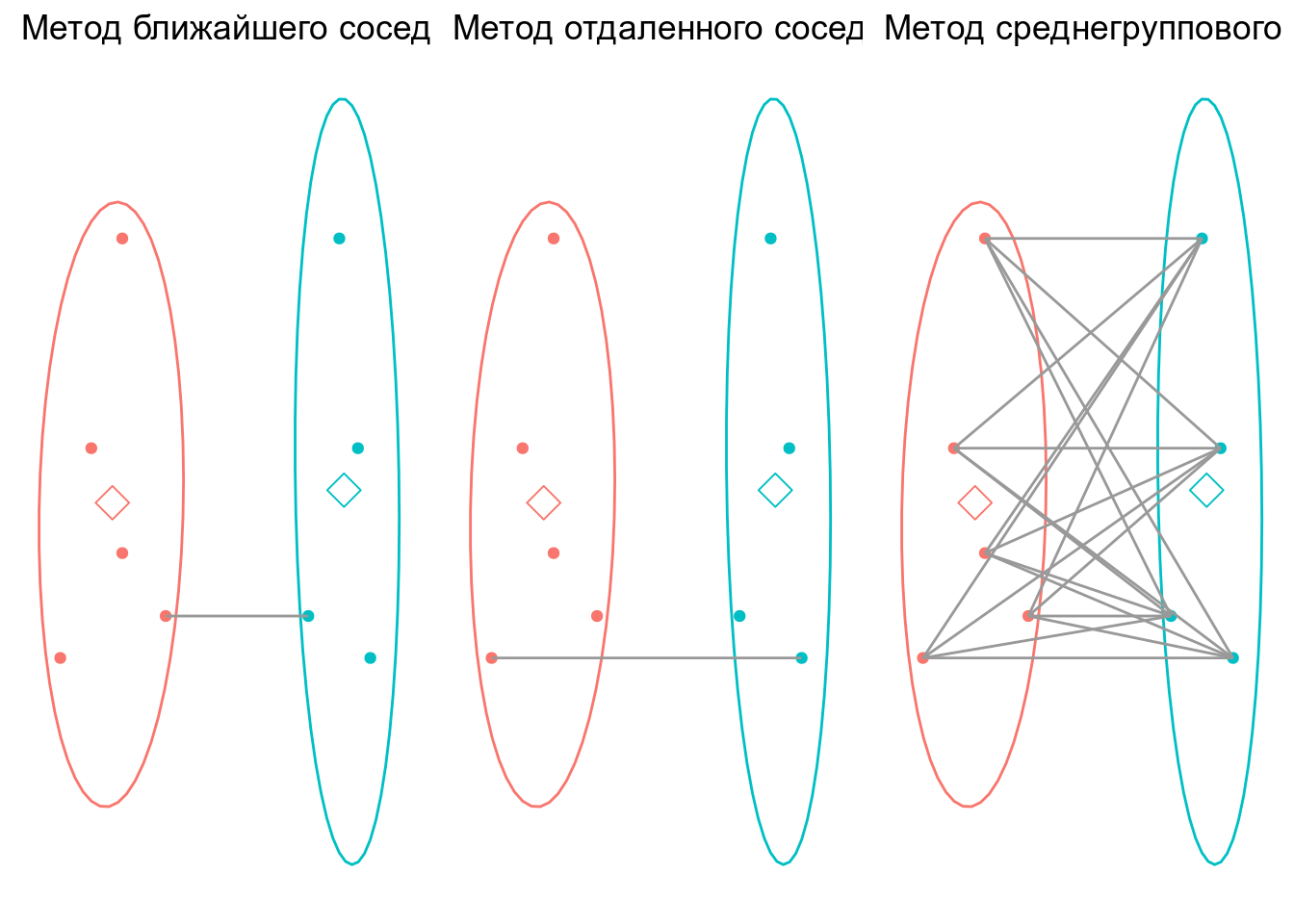
Метод ближайшего соседа (= nearest neighbour = single linkage)
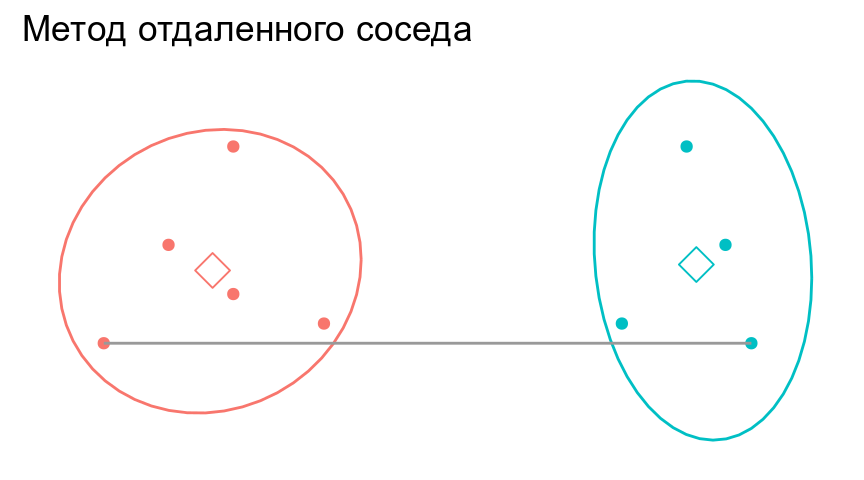
Метод отдаленного соседа (= furthest neighbour = complete linkage)
Метод невзвешенного попарного среднего (= UPGMA = Unweighted Pair Group Method with Arithmetic mean)
Инверсии на дендрограммах
из Borcard et al., 2011
Кластерный анализ в R: гребешки
Вспомним, на чем мы остановились в прошлый раз.
Названия проб в этом файле — длинные непонятные аббревиатуры.
Вместо них нужно создать осмысленные и краткие лейблы для проб.
Информацию о лейблах возьмем из датафрейма с факторами
Чтобы строить деревья для проб, нам понадобится транспонировать исходные данные
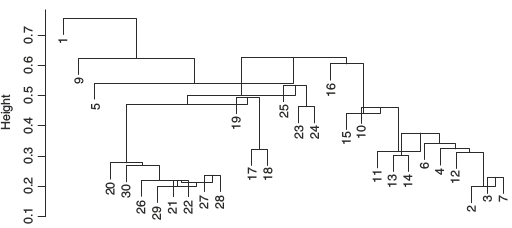
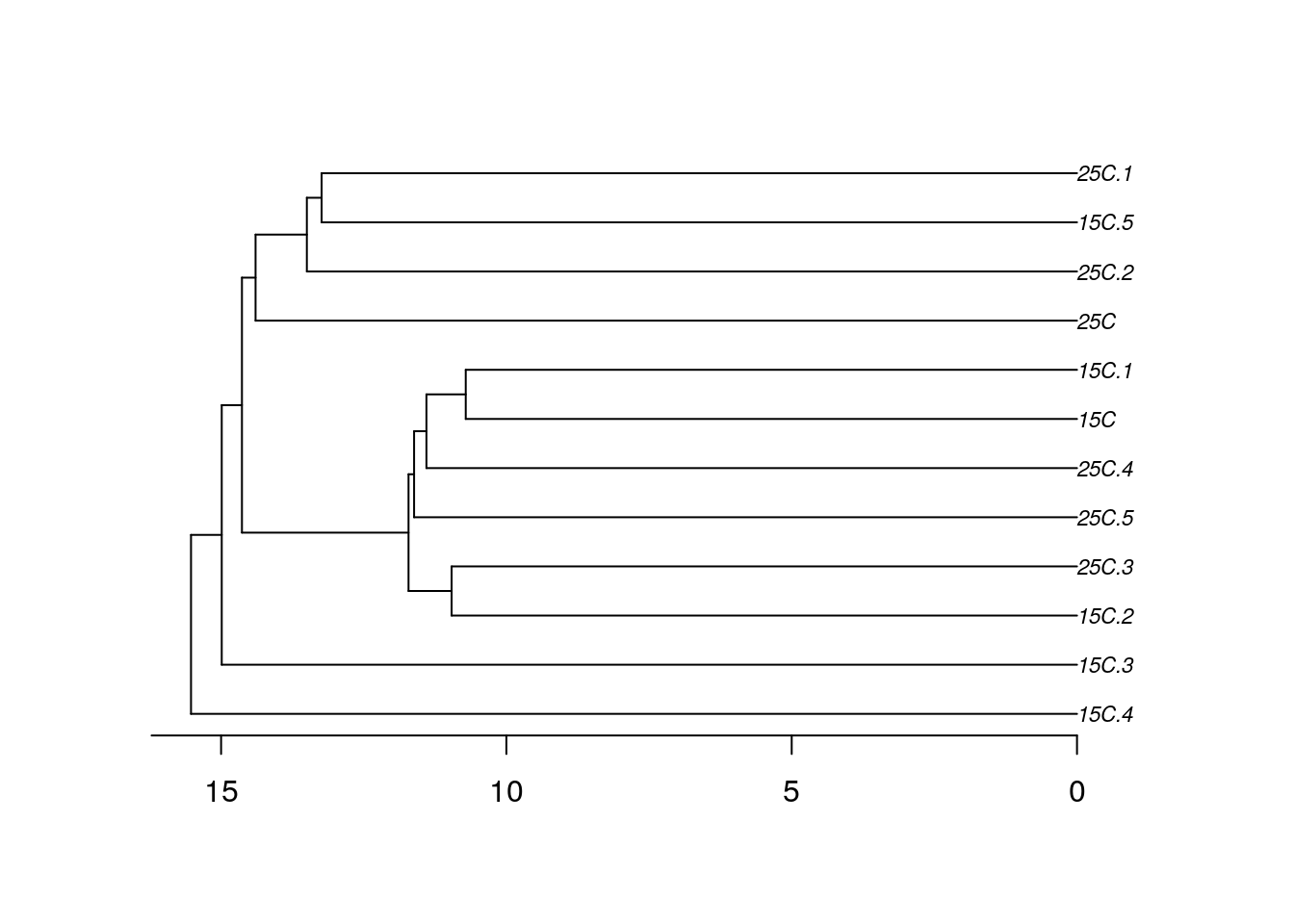
Давайте построим деревья при помощи нескольких алгоритмов кластеризации (по стандартизованным данным, с использованием Евклидова расстояния) и сравним их. Нам понадобится матрица расстояний.
Деревья можно визуализировать при помощи базовой графики, но у нее довольно мало возможностей для настройки внешнего вида.
При желании можно раскрасить лейблы. Это можно сделать вручную, просто передав вектор нужных цветов в том порядке, в котором идут лейблы на дендрограмме.
Чтобы не пришлось вручную создавать вектор цветов, можно попробовать при помощи функции вытащить информацию из лейблов на дендрограмме. Эта функция берет дендрограмму, экстрагирует из нее порядок лейблов, берет первые несколько букв в имени лейбла и на основании этого фактора создает вектор цветов.
Теперь можно легко раскрасить группы на дендрограмме, ориентируясь на первые несколько символов в названии лейбла.
Задание 1
Постройте дендрограммы, описывающие сходство проб, при помощи методов отдаленного соседа и среднегруппового расстояния.
Семантический поиск: от простого сходства Жаккара к сложному SBERT
В материале, переводом которого мы решили поделиться к старту курса о машинном и глубоком обучении, простым языком рассказывается о семантическом поиске, статья охватывает шесть его методов; начиная с простых сходства по Жаккару, алгоритма шинглов и расстояния Левенштейна, автор переходит к поиску с разреженными векторами — TF-IDF и BM25 и заканчивает современными представлениями плотных векторов и Sentence-BERT. Простые примеры сопровождаются кодом и иллюстрациями, а в конце вы найдёте ссылки на соответствующие блокноты Jupyter.
Поиск сходства — одна из самых быстрорастущих областей в ИИ и машинном обучении. По своей сути, это процесс сопоставления релевантных частей информации друг с другом. Велика вероятность, что вы нашли эту статью через поисковую систему — скорее всего, Google. Возможно, вы искали что-то вроде «what is semantic similarity search?» или «traditional vs vector similarity search». Google обработал ваш запрос и использовал многие основные принципы поиска по сходству, о которых рассказывается в этой статье.
Два видео о двух классах подходов
Традиционный поиск
Мы начинаем с лагеря традиций и там находим нескольких ключевых игроков:
Сходство Жаккара.
Алгоритм шинглов.
Расстояние Левенштейна.
Все это показатели отлично работают при поиске сходства, из них мы рассмотрим три самых популярных: сходство по Жаккару, алгоритм шинглов и расстояние Левенштейна.
Сходство Жаккара
Сходство Жаккара — это простая, но иногда мощная метрика сходства. Даны две последовательности A и B: находим число общих элементов в них и делим найденное число на количество элементов обеих последовательностей.
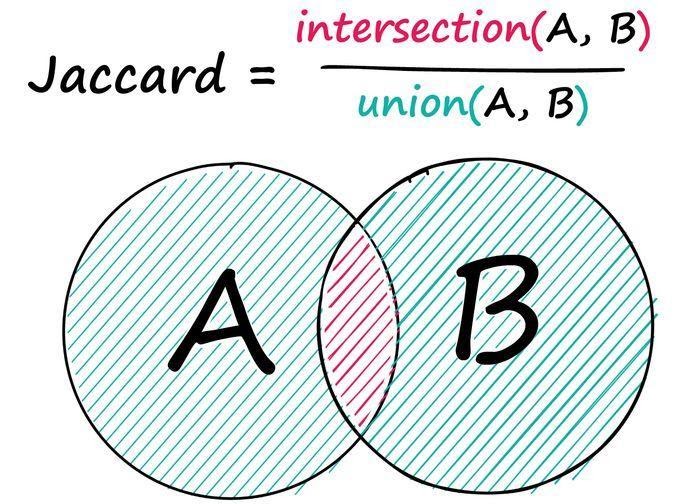
Пример: даны две последовательности целых чисел, запишем:
Здесь мы определили два общих неодинаковых целых числа, 3 и 4 — между двумя последовательностями с общим количеством десяти целых чисел в обеих, где восемь чисел являются уникальными значениями — 2/8 даёт нам оценку сходства по Жаккарду 0,25. Ту же операцию можно выполнить и для текстовых данных: всё, что мы делаем, — заменяем целые числа на токены.

Мы обнаружили, что, как и ожидалось, предложения b и c набрали гораздо больше баллов. Конечно, это не лучшее решение — два предложения, в которых нет ничего общего, кроме слов ‘the’, ‘a’, ‘is’ и т. д., могут получить высокие оценки Жаккара, несмотря на то, что они неодинаковы по смыслу. Эти недостатки могут быть частично устранены с помощью методов предварительной обработки, таких как удаление стоп-слов, стемминг/лемматизация и т. д. Однако, как мы скоро увидим, некоторые методы позволяют полностью избежать этих проблем.
Алгоритм шинглов
Другая похожая техника — алгоритм использует точно такую же логику пересечения/объединения — но с «шинглом». 2-шингловое предложение a будет выглядеть так:
После можно применить тот же расчёт пересечения/объединения между разбитыми на шинглы предложениями:
При помощи двух шинглов находим три совпадающих шингла между предложениями b и c, в результате сходство составляет 0,125.
Расстояние Левенштейна
Другая популярная метрика сравнения двух строк — расстояние Левенштейна — это количество операций, необходимых для преобразования одной строки в другую, вот его формула:

На вид она довольно сложна; если вы её поняли, это прекрасно! Если нет, не волнуйтесь — мы разберём её. Переменные a и b представляют две наши строки, i и j — позиции символов в a и b соответственно. Итак, даны строки:


Это легко! Прекрасный способ понять логику этой формулы — визуализировать алгоритм Вагнера — Фишера, рассчитывающий расстояние Левенштейна при помощи простой матрицы. Мы берём два слова a и b и размещаем их по обеим осям нашей матрицы, включая символ ничего как пустое пространство:

Код инициализации пустой матрицы Вагнера — Фишера:
Переберём все позиции в матрице и применим ту сложную формулу, которую видели ранее. Первый шаг в нашей формуле if min(i, j) = 0 — здесь мы уточняем, не равны ли i и j нулю? Если да, переходим к функции max(i, j), которая присваивает текущей позиции в нашей матрице больше из двух значений — i и j:

Код операций min(i, j) == 0, за которой следует визуализированная выше max(i, j).
С внешними краями нашей матрицы мы разобрались, но нам всё ещё нужно вычислить внутренние значения — именно там будет проходить оптимальный путь. Вернёмся к if min(i, j) = 0 — что, если ни одно из них не равно 0? Затем переходим к сложной части уравнения в разделе min <. Нам нужно вычислить значение для каждой строки, а после взять минимальное значение. Сейчас эти значения известны — они находятся в нашей матрице:

Эта операция в цикле по всей матрице выглядит так:
Полная реализация расчёта расстояния Левенштейна при помощи матрицы Вагнера — Фишера.
Векторное сходство
Для поиска на основе вектора мы обычно используем один из нескольких методов построения векторов:
В тандеме с некоторыми реализациями приблизительных ближайших соседей (ANN) эти векторные методы в мире поиска сходства, если говорить терминами программирования, — минимально жизнеспособные продукты. Рассмотрим подходы на основе TF-IDF, BM25 и BERT, поскольку они являются наиболее распространёнными и охватывают как разреженные, так и плотные векторные представления.
1. TF-IDF
Почтенный дедушка векторного поиска сходства, родившийся ещё в 1970-х годах. Он состоит из двух частей: Term Frequency (TF) и Inverse Document Frequency (IDF). Компонент TF подсчитывает, сколько раз термин встречается в документе, и делит его на общее количество терминов этого же документа.

Это первая половина нашего расчёта, мы имеем частоту запроса в рамках текущего документа f(q, D) в числителе и частоту всех терминов в рамках текущего документа f(t, D) в знаменатели дроби. TF — хороший показатель, но не позволяет нам провести различие между распространёнными и необычными словами. Если бы мы искали слово «the», используя только TF, мы бы присвоили этому предложению ту же релевантность, что и при поиске «bananas». Это хорошо, пока мы не начнём сравнивать документы или искать что-то с помощью длинных запросов. Мы не хотим, чтобы такие слова, как ‘the’, ‘is’ или ‘it’, были оценены так же высоко, как ‘bananas’ или ‘street’.
В идеале хочется, чтобы совпадения между более редкими словами оценивались выше. Для этого мы можем умножить TF на второй член — IDF. Обратная частота документа измеряет, насколько часто встречается слово во всех наших документах.

Здесь три предложения. Вычислив IDF для нашего распространённого слова ‘is’, получаем гораздо меньшее число, чем в случае более редкого слова ‘forest’. Если бы после мы искали оба слова ‘is’ и ‘forest’, то объединили бы TF и IDF следующим образом:
Мы вычисляем оценки TF(‘is’, D) и TF(‘forest’, D) для документов a, b и c. Значение IDF относится ко всем документам, поэтому IDF(‘is’) и IDF(‘forest’) вычисляются только один раз. Затем мы получаем значения TF-IDF для обоих слов в каждом документе путём умножения компонентов TF и IDF. Предложение a набирает наибольшее количество баллов для ‘forest’, а ‘is’ всегда набирает 0, поскольку IDF(‘is’) равно 0.
Это замечательно, но где здесь применяется векторное сходства? Итак, мы берём наш словарный запас (большой список всех слов в нашем наборе данных) и вычисляем TF-IDF для каждого слова.

Чтобы сформировать векторы TF-IDF, мы можем собрать это воедино:
Отсюда мы получаем вектор TF-IDF. Стоит отметить, что словарь легко может иметь более 20 000 слов, поэтому созданные этим методом векторы невероятно разрежены, а это означает, что закодировать какой-либо семантический смысл мы не можем.
2. BM25
Преемник TF-IDF, Okapi BM25, является результатом оптимизации TF-IDF в первую очередь для нормализации результатов на основе длины документа. TF-IDF — отличный инструмент, но он может давать сомнительные результаты, когда мы начинаем сравнивать несколько упоминаний. Если мы возьмём две статьи по 500 слов и обнаружим, что «Черчилль» в статье А упоминается 6 раз, а в статье Б — 12 раз, должны ли мы считать статью А в два раза менее релевантной? Скорее всего, нет. BM25 решает эту проблему путём модификации TF-IDF:

Уравнение выглядит довольно неприятно, но это не что иное, как наша формула TF-IDF с несколькими новыми параметрами! Давайте сравним два компонента TF:

И затем часть IDF, которая даже не вводит никаких новых параметров — она просто переставляет IDF из TF-IDF.

Итак, каков результат этой модификации? Если взять последовательность из 12 лексем и постепенно подавать в неё всё больше и больше «подходящих» лексем, то получим следующие результаты:


Показатель TF-IDF линейно увеличивается с ростом числа релевантных лексем. Таким образом, если частота удваивается — увеличивается и показатель TF-IDF. Звучит круто! Но как реализовать это на Python? Опять же напишем простую и понятную реализацию, как с TF-IDF.
Мы использовали параметры по умолчанию для k и b, и наши результаты выглядят многообещающе. Запрос ‘purple’ соответствует только предложению a, а ‘bananas’ набирает приемлемые баллы и для b, и для c, но для c — немного выше благодаря меньшему количеству слов. Чтобы построить векторы на основе этих данных, сделаем то же самое, что и с TF-IDF.
Опять же, как и в случае с векторами TF-IDF, эти векторы разрежены. Мы не сможем кодировать семантическое [смысловое] значение, вместо этого сосредоточимся на синтаксисе.
Теперь давайте посмотрим, как можно начать рассматривать семантику.
3. BERT
Каждый плотный вектор обычно содержит 768 значений, и мы обычно имеем 512 таких векторов для каждого закодированного BERT предложения. Эти векторы содержат то, что мы можем рассматривать как числовые представления языка. Эти векторы также возможно извлечь (если этого захочется) из разных слоёв, но обычно из последнего слоя. Теперь, имея два правильно закодированных плотных вектора, мы можем использовать метрику сходства, такую как косинусное сходство, чтобы рассчитать теперь уже семантическое сходство. Более выровненные векторы семантически схожи, и наоборот.

Рассмотрим оба варианта, начиная с подхода через transformers и PyTorch, чтобы получить интуитивное представление о построении векторов. Если вы уже использовали библиотеку трансформаторов HF, первые несколько шагов покажутся вам очень знакомыми: инициализируем SBERT и токенизатор, токенизируем наш текст и обработаем токены моделью.
Мы добавили сюда новое предложение, предложение g несёт тот же семантический смысл, что и b, — без тех же ключевых слов. Из-за отсутствия общих слов все наши предыдущие методы не смогли бы найти сходство между этими двумя последовательностями — запомните это на будущее.
У нас есть векторы длины 768, но это не векторы предложений, так как мы имеем векторное представление каждой лексемы в последовательности (поскольку мы работаем SBERT, их здесь 128, а в случае BERT их 512). Для создания вектора предложений нам необходимо выполнить вычислить среднее значение.
Первое, что мы делаем, — умножаем каждое значение в тензоре embeddings на соответствующее значение attention_mask. Маска attention_mask содержит единицы там, где у нас есть «настоящие токены» (например, не токен заполнения), и нули в других местах — эта операция позволяет нам игнорировать ненастоящие токены.
И вот наши векторы предложений, при помощи которых мы можем измерить сходство, вычислив косинусное сходство между всеми векторами.
Визуализировав массив, можно легко определить предложения с более высоким уровнем сходства:

Теперь вспомните замечание о том, что предложения b и g имеют по сути одинаковый смысл, но не имеют ни одного одинакового ключевого слова. Мы надеемся, что SBERT с его превосходными семантическими представлениями языка определит эти два предложения как похожие — и вот, пожалуйста, сходство между ними составляет 0,66 балла (обведено выше). Итак, альтернативный (простой) подход заключается в применении SBERT. Чтобы получить точно такой же результат, как выше, напишем:
Что, конечно, гораздо проще. На этом завершаем прогулку по истории с Жаккаром, Левенштейном и Bert!
[1] Market Capitalization of Alphabet (GOOG), Companies Market Cap.
[2] N. Reimers, I. Gurevych, Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks (2019), Proceedings of the 2019 Conference on Empirical Methods in 2019.