Коническая проекция для чего

Коническая проекция

В конической проекции изображение строится на боковой поверхности конуса, секущего земной шар по двум параллелям или касательного к нему. Вершина конуса лежит на продолжении земной оси.

Параллели нормальной сетки являются дугами концентрических окружностей, а меридианы — их радиусами, углы между которыми пропорциональны соответствующим разностям долгот.

Искажения не зависят от долготы.

В равноугольной конической проекции меридианы сетки растянуты в такой же степени, в какой растянуты ее параллели.

Ссылки

Полезное

Смотреть что такое «Коническая проекция» в других словарях:

коническая проекция — Картографическая проекция, в которой параллели изображаются дугами концентрических окружностей, а меридианы – прямыми, расходящимися из общего центра параллелей, углы между которыми равны разностям их долгот. → Рис. 67 … Словарь по географии

коническая проекция — kūginė projekcija statusas T sritis fizika atitikmenys: angl. conic projection; conical projection vok. Kegelprojektion, f; konische Projektion, f rus. коническая проекция, f pranc. projection conique, f … Fizikos terminų žodynas

коническая картографическая проекция — коническая проекция Картографическая проекция, в которой параллели нормальной сетки дуги концентрических окружностей, а меридианы их радиусы, углы между которыми пропорциональны соответствующим разностям долгот. [ГОСТ 21667 76] Тематики… … Справочник технического переводчика

Проекция Альберса — … Википедия

Равновеликая проекция — Равновеликая проекция. Равновеликая проекция один из основных типов картографических проекций. Не искажает площадей и сохраняет на всей карте единый масштаб площадей, благодаря чему площади фигур на карте пропорциональны площадям… … Википедия

КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображение всей поверхности земного эллипсоида или какой либо ее части на плоскость, получаемое в основном с целью построения карты. К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель… … Математическая энциклопедия

легенда к географическим картам — НАСЕЛЕННЫЕ ПУНКТЫ :: более 1 млн. жителей :: от 250 тыс. до 1 млн. жителей :: от 100 тыс. до 250 тыс. жителей :: менее 100 тыс. жителей Прописными буквами выделены столицы. ПУТИ СООБЩЕНИЯ :: Железные дороги … Географическая энциклопедия

Карты географические — (истор.) Первоначальное понятие о К. можно встретить даже у дикарей, особенно живущих по берегам и о вам и имеющих более или менее ясное представление об окружающих их территорию местностях. Путешественники, расспрашивавшие эскимосов С. Америки и … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Конические проекции.

Основные виды картографических проекций.

В авиации карты используются как при подготовке к полету, так и в процессе полета. При подготовке к полету карта необходима для прокладки и изучения маршрута полета; измерения путевых углов и расстояний между пунктами маршрута; определения географических координат пунктов; нанесения точек расположения радиотехнических средств, обеспечивающих полет; получения данных о магнитном склонении в районе полета; изучения рельефа местности.

В полете карта применяется для ведения визуальной и радиолокационной ориентировки; контроля пути и прокладки линий положения самолета; определения навигационных элементов полета.

Карты нужны также службе движения для руководства полетами и контроля за их выполнением. Авиационные карты создаются в определенных картографических проекциях.

Картографической проекцией называется способ изображения земной поверхности на плоскости. Сущность любой картографической проекции состоит в том, что поверхность земного шара переносится сначала на глобус определенного размера, а затем с глобуса по намеченному способу на плоскость.

При переносе поверхности Земли с глобуса на плоскость приходится в одних местах растягивать изображения, а в других сжимать, т.е. допускать искажения. Каждая проекция имеет определенную степень искажения длин, направлений и площадей и определенный вид сетки меридианов и параллелей. Выбор проекции для построения карты зависит от того, каким требованиям должна отвечать данная карта.

По виду сетки меридианов и параллелей все картографические проекции делятся на конические (поликонические) цилиндрические, и азимутальные.

Конические проекции.

Конические проекции могут строиться на касательном или секущем конусе.

В зависимости от расположения оси конуса относительно оси вращения глобуса конические проекции могут быть нормальные, поперечные и косые. Большинство авиационных карт конической проекции построено в нормальной равноугольной проекции на касательном или секущем конусах.

Равноугольная коническая проекция на касательном конусе. Построение этой проекции (рис. 1) наглядно можно объяснить следующим образом. Все меридианы выпрямляют до соприкосновения с боковой поверхностью конуса. При этом все параллели, кроме параллели касания, будут растягиваться до размеров окружности конуса. Для того чтобы сделать проекцию равноугольной и сохранить подобие фигур,

Рисунок 1. Равноугольная коническая проекция на касательном конусе

производят растягивание меридианов в такой степени, в какой были растянуты параллели в данной точке карты. Затем конус разрезается по образующей и разворачивается на плоскость. Карты в равноугольной конической проекции на касательном конусе имеют следующие свойства:

— меридианы изображаются в виде прямых, сходящихся к полюсу;

— угол схождения меридианов определяется по формуле

,

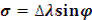
— параллели имеют вид дуг концентрических окружностей, расстояния между которыми увеличиваются по мере удаления от параллели касания;

— на параллели касания искажения длин отсутствуют, а в полосе ±5° от этой параллели они незначительны и в практике не учитываются;

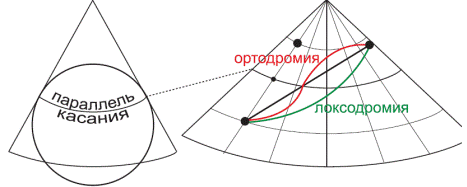
— локсодромия изображается кривой линией, обращенной своей выпуклостью к экватору;

— ортодромия для расстояний до 1200 км изображается прямой линией, а для больших расстояний имеет вид кривой, обращенной своей выпуклостью в сторону более крупного масштаба.

В равноугольной конической проекции на касательном конусе издаются бортовые карты масштабов 1:2000000; 1:2500000; 1:3000000; 1:4000000 и обзорная карта масштаба 1:5000000.

Рисунок 2. Равноугольная коническая проекция на секущем конусе

Источник

Картографическая коническая проекция: характеристики, достоинства, недостатки

Содержание:

В конических проекциях поверхности Земли меридианы становятся радиальными линиями с центром в вершине и равным угловым интервалом, а параллели Земли становятся дугами окружности, концентричными по отношению к вершине.

На рисунке 1 видно, что коническая проекция не позволяет представить оба полушария. Кроме того, ясно видно, что расстояния искажены в сторону от параллелей, пересекающих конус.

По этим причинам этот тип проекции используется для представления регионов средних широт, протяженных с востока на запад и меньшей протяженности с севера на юг. Так обстоит дело в континентальной части Соединенных Штатов.

Преимущество

Землю можно аппроксимировать сферой с радиусом 6378 км, учитывая, что все массы суши и воды находятся на этой большой сфере. Речь идет о преобразовании этой поверхности, которая покрывает объект в трех измерениях, например, сферу, в другой объект в двух измерениях: плоскую карту. Это приносит недостаток, заключающийся в том, что криволинейная поверхность искажается при ее проецировании на плоскость.

Картографические проекции, такие как коническая проекция, пытаются решить эту проблему с минимальной потерей точности. Следовательно, есть несколько вариантов построения проекции в зависимости от характеристик, которые вы хотите выделить.

Транспортировать глобус повсюду непросто, так как он занимает много места. Также невозможно увидеть всю поверхность Земли сразу, и невозможно воспроизвести все детали на масштабной модели.

Возможны следующие варианты проецирования:

— Проецировать на самолет или

— На цилиндре, который может разворачиваться в прямоугольную плоскость.

— Наконец-то на конусе.

Преимущество конической системы проецирования состоит в том, что она точна по сравнению с параллелями, выбранными для пересечения конуса.

Кроме того, он сохраняет ориентацию по меридианам практически неизменной, хотя может немного исказить шкалу по меридианам для широт, далеких от стандартных или опорных параллелей. Вот почему он подходит для представления очень больших стран или континентов.

Эквидистантная коническая проекция

Это коническая проекционная система, первоначально использовавшаяся Птолемеем, греческим географом, жившим между 100-170 годами нашей эры. Позже в 1745 году его улучшили.

Часто используется в атласах регионов с промежуточными широтами. Он подходит для отображения областей с несколькими градусами широты, принадлежащих одному из экваториальных полушарий.

В этой проекции расстояния истинны по меридианам и по двум стандартным параллелям, то есть параллелям, выбранным для пересечения с конусом проекции.

В эквидистантной конической проекции точка на сфере проходит радиально до пересечения с касательным или секущим конусом, принимая центр сферы за центр проекции.

Недостатки

Основным недостатком конической проекции является то, что она неприменима к экваториальным областям.

Кроме того, коническая проекция не подходит для картографирования больших регионов, а скорее отдельных областей, таких как Северная Америка.

Коническая проекция Альберта

Используйте две стандартные параллели и сохраните площадь, но не масштаб и форму. Этот тип конического выступа был введен Х. К. Альберсом в 1805 году.

Все области на карте пропорциональны земным. В ограниченных регионах направления относительно точны. Расстояния соответствуют расстояниям от сферической поверхности на стандартных параллелях.

В Соединенных Штатах эта система проекции используется для карт, показывающих границы штатов Союза, для которых 29,5º с.ш. и 45,5º с.ш. выбраны в качестве стандартных параллелей, что приводит к максимальной ошибке шкалы в 1, 25%.

Карты, сделанные с помощью этой проекции, не сохраняют углы, соответствующие углам сферы, а также перспективу или равноудаленность.

Конформная коническая проекция Ламберта

Он был предложен в 1772 году одноименным швейцарским математиком и географом. Его основная характеристика заключается в том, что он использует касательный или секущий конус к сфере, а проекция сохраняет неизменными углы. Эти качества делают его очень полезным в аэронавигационных картах.

Геологическая служба США (USGS) использует проекцию конуса Ламберта. В этой проекции расстояния истинны по стандартным параллелям.

В конической проекции Ламберта направления остаются достаточно точными. Области и формы слегка искажаются в положениях, близких к стандартным параллелям, но изменение формы и площади увеличивается с расстоянием между ними.

Поскольку целью этой проекции является поддержание направлений и углов, равных исходным на сфере или эллипсоиде, не существует геометрического метода их получения, в отличие от эквидистантной проекции Птолемея.

Скорее, это метод аналитического проектирования, основанный на математических формулах.

Базовые карты USGS для 48 континентальных штатов используют 33º и 45º с.ш. в качестве стандартных параллелей, что дает максимальную ошибку карты в 2,5%.

Для навигационных карт на Аляске используются базовые параллели: 55 ° и 65 °. Вместо этого в национальном атласе Канады используются 49º и 77º северной широты.

Ссылки

5 измерений устойчивости и их характеристики

Источник

Справка

Самая простая коническая проекция проходит по касательной к глобусу вдоль линии широты. Эта линия называется стандартной параллелью. Меридианы проецируются на коническую поверхность, сходясь на вершине или в точке конуса. Параллели проецируются на коническую поверхность как кольца. Конус затем “рассекается” вдоль любого меридиана для создания конечной конической проекции, в которой имеются прямые сходящиеся меридианы и параллели, представленные концентрическими окружностями. Меридиан, противолежащий линии сечения, становится центральным меридианом.

В целом, чем дальше от стандартной параллели, тем больше искажение. Соответственно, отсечение верхушки конуса создает более точную проекцию. Этого можно достичь, если не использовать полярную область при проецировании объектов. Конические проекции используются для среднеширотных зон, имеющих ориентацию с востока на запад.

Более сложные конические проекции соприкасаются с поверхностью глобуса в двух местах. Эти проекции называются секущими коническими проекциями и определяются двумя стандартными параллелями. Можно также определить секущую проекцию с помощью одной стандартной параллели и коэффициента масштабирования. Характер искажений при секущих проекциях различается для районов, расположенных между стандартными параллелями, и для районов, расположенных за их пределами. Как правило, секущая проекция дает меньшее суммарное искажение, чем касательная проекция. В еще более сложных конических проекциях ось конуса не совпадает с полярной осью глобуса. Такие проекции называются косыми.

Изображение географических объектов зависит от расстояния между параллелями. При их равном удалении друг от друга проекция получается равнопромежуточной в направлении с севера на юг, но не равноугольной и не равновеликой. Примером такого типа проекций является Равнопромежуточная Коническая проекция. Для небольших областей общее искажение минимально. В равноугольной конической проекции Ламберта расстояние между центральными параллелями меньше, чем у параллелей ближе к границам, и не искажаются формы малых географических объектов на мелкомасштабных и крупномасштабных картах. В равновеликой конической проекции Альберса параллели вблизи северного и южного полюса расположены ближе друг к другу, чем центральные параллели, и проекция отображает эквивалентные площади.

Источник

Ликбез по картографическим проекциям с картинками

Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.

Легкое введение

Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.

Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.

Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.

Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.

Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.

Проблема

Начнем с того, что же это за самые распространенные проекции, и что с ними не так.

Первая проекция — так называемая «Географическая», она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).

Другая весьма популярная проекция — «проекция Меркатора», Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).

На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.

Варианты решения

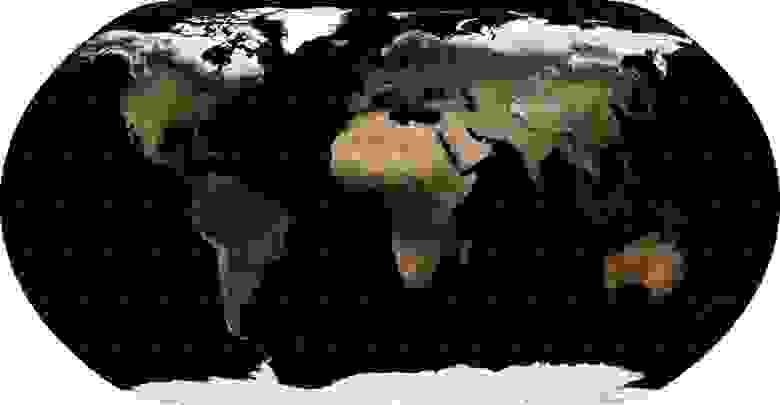
Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами: «Тройная проекция Винкеля» Winkel Tripel WKID:54042 PROJ.4:wintri, «проекция Робинсона» Robinson projection WKID:54030 PROJ.4:robin, «проекция Каврайского» (Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.

Вот так описание этой проекции выглядит в формате ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,0],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]

Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.

Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:

А вот измененное для этого случая описание в ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,11],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]

В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.

11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.

Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.

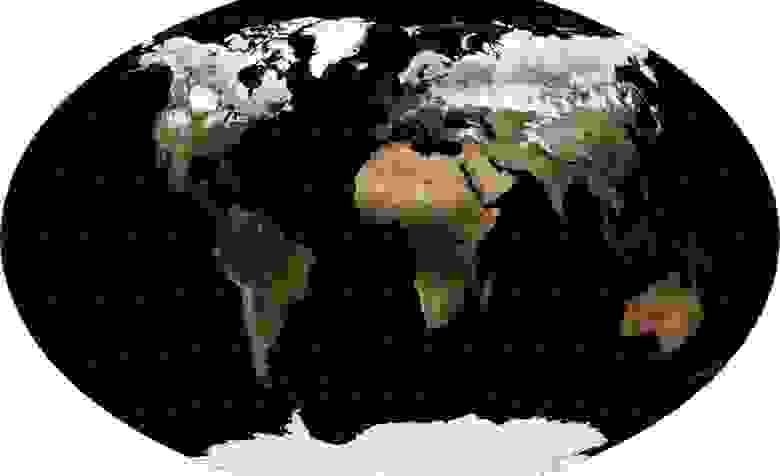
Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции — «проекцию Моллвейде», Mollweide projection WKID:54009 PROJ.4:moll.

Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.

Самым молодым конкурентом этих проекций является проекция Natural Earth PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.

Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.

Немного экзотики и специальных случаев

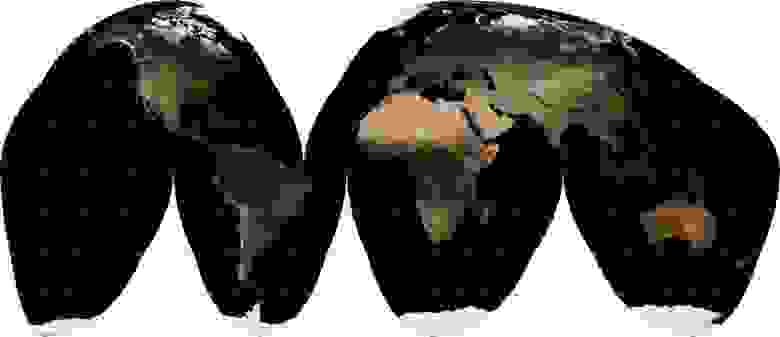
Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была «Разрывная гомолосинусоидальная проекция Гуда» Interrupted Goode Homolosine projection WKID:54052.

Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.

На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.

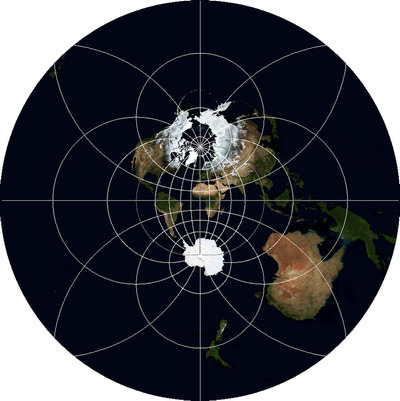
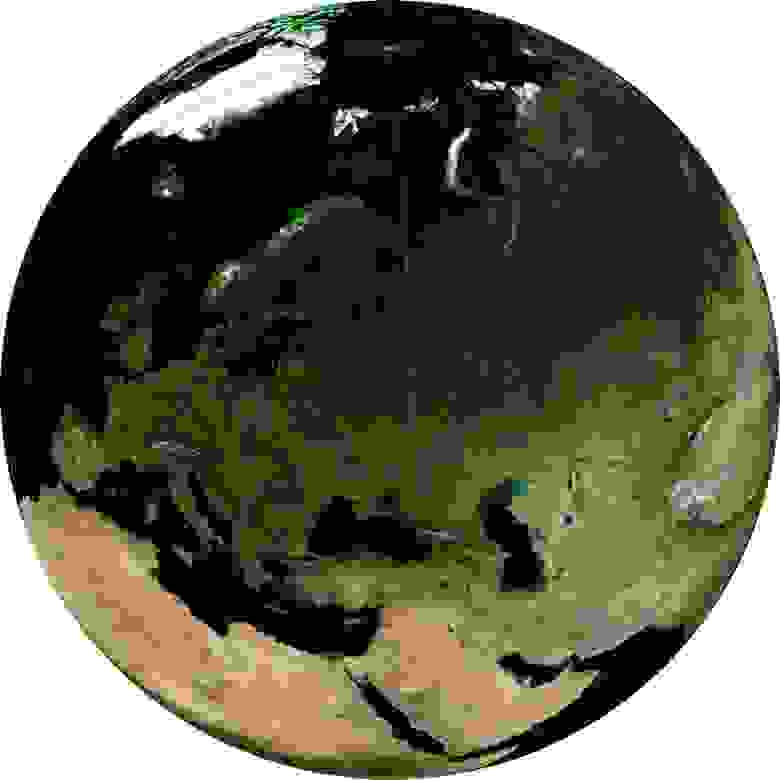
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется «Ортографическая проекция» Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.

Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.

Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.

Источник