Корень 43200 чему равен
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.
Сейчас изучают числа:
Число 43200
Сорок три тысячи двести
RGB(0, 168, 192) или #00A8C0
(возможное основание)
доброжелательность, благородство, прощение, раскаяние, благодарность, исцеление, щедрость, великодушие
Описание числа 43200
Неотрицательное вещественное пятизначное число 43200 – составное. Произведение цифр числа: 0. 84 — количество делителей. 43200 и 0.000023148148148148147 являются взаимно обратными числами.
Число 43200 можно представить произведением простых чисел: 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 * 5 * 5.
Число 43200 не является числом Фибоначчи.
Число секунд 43200 можно представить как 12 часов ноль секунд. Нумерологическая цифра этого числа — 9.
Число 43200
Основные свойства числа 43200:
Четное натуральное целое положительное число. Число примерно равно 43.2 тыс.. Число 43200 прописью сорок три тысячи двести. Сумма цифр числа равна 9.
Квадрат числа (вторая степень) 43200 равен 1866240000. Куб числа (третья степень) равен 80621568000000. Квадратный корень числа (корень 2-й степени) 43200 равен 207.8461. Кубический корень числа (корень 3-й степени) равен 35.0882.
Число 43200 является составным и имеет 84 делителя: 1, 43200, 2, 21600, 3, 14400, 4, 10800, 5, 8640, 6, 7200, 8, 5400, 9, 4800, 10, 4320, 12, 3600, 15, 2880, 16, 2700, 18, 2400, 20, 2160, 24, 1800, 25, 1728, 27, 1600, 30, 1440, 32, 1350, 36, 1200, 40, 1080, 45, 960, 48, 900, 50, 864, 54, 800, 60, 720, 64, 675, 72, 600, 75, 576, 80, 540, 90, 480, 96, 450, 100, 432, 108, 400, 120, 360, 135, 320, 144, 300, 150, 288, 160, 270, 180, 240, 192, 225, 200, 216.
Десятичное число 43200 в двоичной системе счисления 1010100011000000 (двоичный вид), в восьмеричной системе счисления 124300, в шестнадцатеричной системе счисления A8C0. Римскими цифрами (римское написание) число пишется X X X X MMMCC.
Свойство числа
Длина числа
Цифры в числе
Сумма цифр
Произведение цифр
Произведение цифр без ноля
Процент
Умножение
Деление
/2 21600 /3 14400 /4 10800 /5 8640 /6 7200 /7 6171.4285714286 /8 5400 /9 4800 /10 4320 /11 3927.2727272727 /12 3600 /13 3323.0769230769 /14 3085.7142857143 /15 2880 /16 2700 /17 2541.1764705882 /18 2400 /19 2273.6842105263 /20 2160
Чётность
Простое число?
Следующее простое число
Плоское число?
Полупростое число?
Линейное число?
Квадратное пирамидальное число?
Треугольное число
Избыточное число?
Число Фибоначчи?
Число Харшад?
Количество делителей
Делители
Сумма делителей
Факторизация
Степени числа
2 1866240000 3 80621568000000 4 3482851737600000000 5 150459195064320000000000 6 6499837226778624000000000000 7 280792968196836556800000000000000 8 12130256226103339253760000000000000000 9 524027068967664255762432000000000000000000 10 22637969379403095848937062400000000000000000000
Корни
2 √ 207.84609690827 3 √ 35.088212858554 4 √ 14.416868484809 5 √ 8.454671719826 6 √ 5.9235304387295 7 √ 4.5942218590438 8 √ 3.7969551597048 9 √ 3.2738121009617 10 √ 2.9076918199538 2.6388069141928
Квадратный корень с остатком
Полный квадрат?
Полный куб?
Натуральный логарифм
Десятичный логарифм
Двоичный логарифм
Тригонометрические функции и углы
Золотое сечение
× φ 69899.068313995 / φ 26699.068313995
43200 градус
радиан 753.982 градиан 48000 угловая минута 2592000 угловая секунда 155520000
43200 радиан
градус 2475177.675 градиан 2750197.417 угловая минута 148510660.498 угловая секунда 8910639629.875
Синус
Косинус
Тангенс
Котангенс
Гиперболический синус
градус INF радиан INF
Гиперболический косинус
градус INF радиан INF
Гиперболический тангенс
π ×43200 135716.80263508 2× π ×43200 271433.60527016 2× π ×43200 2 11725931747.671
Число 43200 в других системах счисления
Римское написание
Двоичная система счисления
Шестнадцатеричная система счисления
Восьмеричная система счисления
Как пишется число 43200 на других языках
На английском языке
forty-three thousand two hundred
по цифрам: four three two zero zero
На испанском языке
cuarenta y tres mil doscientos
по цифрам: cuatro tres dos cero cero
На итальянском языке
quarantatre mila duecento
по цифрам: quattro tre due zero zero
На немецком языке
dreiundvierzig tausend zweihundert
по цифрам: vier drei zwei null null
На французском языке
quarante-trois mille deux cents
по цифрам: quatre trois deux zero zero
На португальском языке
quarenta e três mil e duzentos
по цифрам: quatro tres dois zero zero
На китайском языке
四万三千二百
по цифрам: 四 三 二 零 零
На русском языке
сорок три тысячи двести
по цифрам: четыре три два ноль ноль
На латыни
по цифрам: quattuor tres duo nihil nihil
Конвертация времени, длины, веса, скорости и температуры
Конвертация времени
43200 миллисекунд (мс) это 43.2 секунды (с), 0.72 минут (мин), 0.012 часов (ч).
43200 секунд (с) это 43200000 миллисекунд (мс), 720 минут (мин), 12 часов (ч), 0.5 дней.
43200 минут (мин) это 2592000 секунд (с), 720 часов (ч), 30 дней, 4.286 недели, 1 месяц.
43200 часов (ч) это 155520000 секунд (с), 2592000 минут (мин), 1800 дней, 257.143 недель, 60 месяцев, 4.932 года.
43200 дней это 3732480000 секунд (с), 62208000 минут (мин), 1036800 часов (ч), 6171.429 неделя, 1440 месяцев, 118.356 лет.
43200 недель это 435456000 минут (мин), 7257600 часов (ч), 302400 дней, 10080 месяцев, 830.769 лет.
43200 месяцев это 1866240000 минут (мин), 31104000 часов (ч), 1296000 дней, 185760 недель, 3600 лет.
43200 лет это 22705920000 минут (мин), 378432000 часов (ч), 15768000 дней, 2246400 недель, 518400 месяцев.
Конвертация длины и расстояния
43200 миллиметров (мм) это 4320 сантиметров (см), 43.2 метра (м), 0.043 километров (км); 1700.787 дюймов, 141.732 фут, 47.244 ярдов, 0.027 миль, 0.023 морских миль.
43200 сантиметров (см) это 432000 миллиметров (мм), 432 метра (м), 0.432 километров (км); 17007.874 дюймов, 1417.323 футов, 472.441 ярда, 0.268 миль, 0.233 морских миль.
43200 метров (м) это 43200000 миллиметров (мм), 4320000 сантиметров (см), 43.2 километра (км); 1700784 дюйма, 141739.2 футов, 47260.8 ярдов, 26.843 миль, 23.326 морские мили.
43200 километров (км) это 43200000000 миллиметров (мм), 4320000000 сантиметров (см), 43200000 метров (м); 1700787412.8 дюймов, 141732288 футов, 47244081.6 ярд, 26848.975 миль, 23326.134 морских миль.
43200 дюймов это 1097280 миллиметров (мм), 109728 сантиметров (см), 1097.282 метров (м), 1.097 километр (км); 3600 футов, 1200 ярдов, 0.682 миль, 0.592 морских миль.
43200 футов это 13167360 миллиметров (мм), 1316736 сантиметров (см), 13166.717 метров (м), 13.167 километров (км); 518400 дюймов, 14400 ярдов, 8.182 миль, 7.11 морских миль.
43200 ярдов это 39502080 миллиметров (мм), 3950208 сантиметров (см), 39488.117 метров (м), 39.502 километров (км); 1555200 дюймов, 129600 футов, 24.545 мили, 21.329 морская миля.
43200 миль это 69523660800 миллиметров (мм), 6952366080 сантиметров (см), 69523660.8 метров (м), 69508.8 километров (км); 2737152000 дюймов, 228096000 футов, 76032000 ярдов, 37532.58 морские мили.
43200 морских миль это 80006400000 миллиметров (мм), 8000640000 сантиметров (см), 80006400 метров (м), 80006.4 километров (км); 3149858275.2 дюймов, 262488168 футов, 87496070.4 ярдов, 49723.2 мили.
Конвертация веса и массы
43200 миллиграммов (мг) это 216 карат (кар), 43.2 грамма (г), 0.043 килограммов (кг), 1.524 унция, 0.095 фунтов.
43200 граммов (г) это 43200000 миллиграммов (мг), 216000 карат (кар), 43.2 килограмма (кг), 1523.81 унции, 95.24 фунтов.
43200 карат (кар) это 8640000 миллиграммов (мг), 8640 граммов (г), 8.64 килограммов (кг), 304.766 унции, 19.048 фунтов.
43200 килограммов (кг) это 43200000000 миллиграммов (мг), 216000000 карат (кар), 43200000 граммов (г), 1523836.8 унций, 95256 фунтов.
43200 унций это 1224699393.6 миллиграмма (мг), 6091200 карат (кар), 1224720 граммов (г), 1224.698 килограмма (кг), 2700 фунтов.
43200 фунтов это 19595190384 миллиграмма (мг), 97975958.4 карат (кар), 19595174.4 грамма (г), 19591.837 килограмм (кг), 691200 унций.
Конвертация скорости движения
43200 километров/час (км/ч) это 12000 метров/секунду (м/с), 26848.975 миль/час, 23326.134 узлов (уз).
43200 метров/секунду (м/с) это 155520 километров/час (км/ч), 96638.4 миль/час, 83980.8 узлов (уз).
43200 миль/час это 69508.8 километров/час (км/ч), 19311.578 метров/секунду (м/с), 37532.58 узла (уз).
43200 узлов (уз) это 80006.4 километров/час (км/ч), 22222.222 метра/секунду (м/с), 49723.2 мили/час.
Конвертация температуры
43200 градусов по Цельсию (°C) это 77792 градуса по Фаренгейту (°F) и 43473.15 градуса по Кельвину (K).
43200 градусов по Фаренгейту (°F) это 23982.22 градуса по Цельсию (°C) и 24255.37 градусов по Кельвину (K).
43200 градусов по Кельвину (K) это 42926.85 градусов по Цельсию (°C) и 77300.33 градусов по Фаренгейту (°F).
Что такое квадратный корень
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
Это два нетождественных друг другу выражения.
Из выражения x 2 = 16 следует, что:
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
Ищем в таблице число 7396.
Ищем в таблице число 9025.
Ищем в таблице число 1600.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
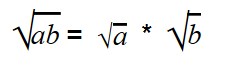 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
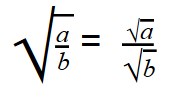 |
Примеры:
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
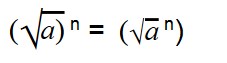 |
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10
Вычислить квадратный корень из числа

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
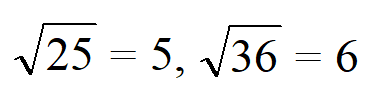
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 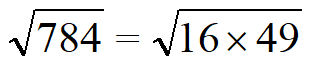 |
| Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 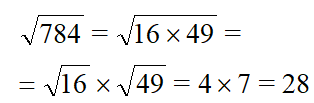 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 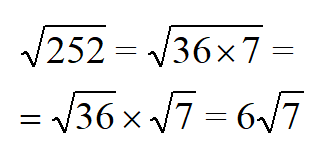 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76 7. |
| Вычисляем корень | 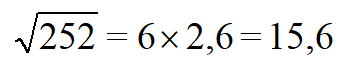 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. |  |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 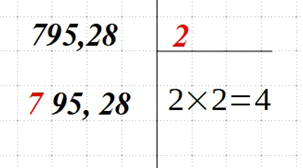 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 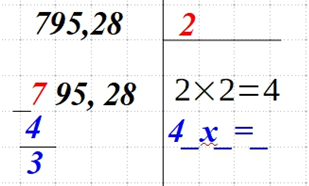 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 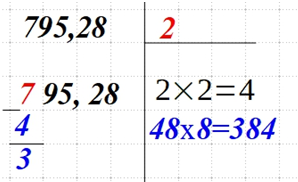 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 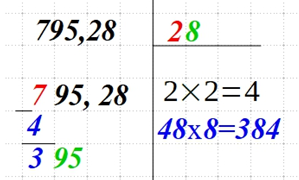 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 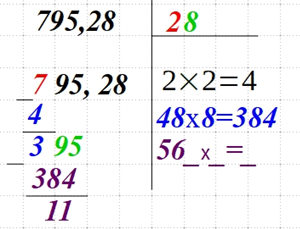 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 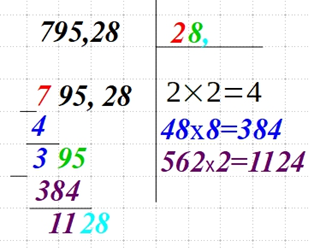 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 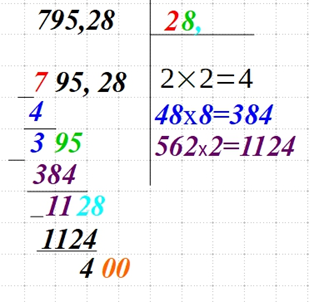 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.




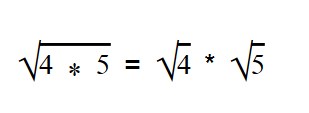
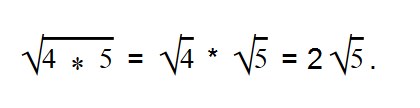


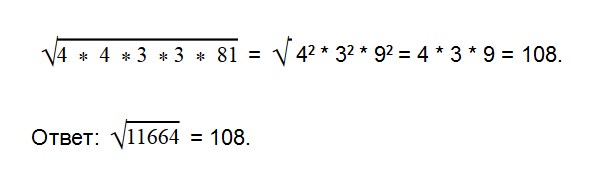






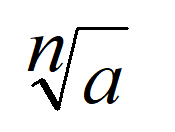
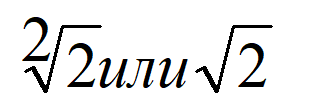
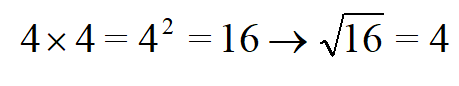
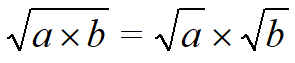
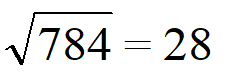
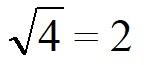
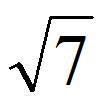 между 2 и 4.
между 2 и 4.