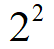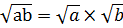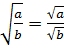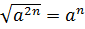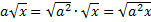Корень 7056 чему равен
Число 7056
Основные свойства числа 7056:
Четное натуральное целое положительное число. Число примерно равно 7.1 тыс.. Число 7056 прописью семь тысяч пятьдесят шесть. Сумма цифр числа равна 18.
Квадрат числа (вторая степень) 7056 равен 49787136. Куб числа (третья степень) равен 351298031616. Квадратный корень числа (корень 2-й степени) 7056 равен 84. Кубический корень числа (корень 3-й степени) равен 19.1802.
Число 7056 является составным и имеет 45 делителей: 1, 7056, 2, 3528, 3, 2352, 4, 1764, 6, 1176, 7, 1008, 8, 882, 9, 784, 12, 588, 14, 504, 16, 441, 18, 392, 21, 336, 24, 294, 28, 252, 36, 196, 42, 168, 48, 147, 49, 144, 56, 126, 63, 112, 72, 98, 84.
Десятичное число 7056 в двоичной системе счисления 1101110010000 (двоичный вид), в восьмеричной системе счисления 15620, в шестнадцатеричной системе счисления 1B90. Римскими цифрами (римское написание) число пишется V MMLVI.
Свойство числа
Длина числа
Цифры в числе
Сумма цифр
Произведение цифр
Произведение цифр без ноля
Процент
Умножение
Деление
/2 3528 /3 2352 /4 1764 /5 1411.2 /6 1176 /7 1008 /8 882 /9 784 /10 705.6 /11 641.45454545455 /12 588 /13 542.76923076923 /14 504 /15 470.4 /16 441 /17 415.05882352941 /18 392 /19 371.36842105263 /20 352.8
Чётность
Простое число?
Следующее простое число
Плоское число?
Полупростое число?
Линейное число?
Квадратное пирамидальное число?
Треугольное число
Избыточное число?
Число Фибоначчи?
Число Харшад?
Количество делителей
Делители
Сумма делителей
Факторизация
Обратное число
Степени числа
2 49787136 3 351298031616 4 2478758911082496 5 17490122876598091776 6 123410307017276135571456 7 870783126313900412592193536 8 6144245739270881311250517590016 9 43353797936295338532183652115152896 10 305904398238499908683087849324518834176
Корни
2 √ 84 3 √ 19.180187896644 4 √ 9.1651513899117 5 √ 5.8845290942271 6 √ 4.3795191398879 7 √ 3.5464519635232 8 √ 3.0274001040351 9 √ 2.6768104503763 10 √ 2.4258048343235 2.2380457551366
Квадратный корень с остатком
Полный квадрат?
Полный куб?
Натуральный логарифм
Десятичный логарифм
Двоичный логарифм
Тригонометрические функции и углы
Золотое сечение
× φ 11416.847824619 / φ 4360.8478246193
7056 градус
радиан 123.15 градиан 7840 угловая минута 423360 угловая секунда 25401600
7056 радиан
градус 404279.02 градиан 449198.911 угловая минута 24256741.215 угловая секунда 1455404472.88
Синус
Косинус
Тангенс
Котангенс
Гиперболический синус
градус 1.522380017833E+53 радиан INF
Гиперболический косинус
градус 1.522380017833E+53 радиан INF
Гиперболический тангенс
π ×7056 22167.07776373 2× π ×7056 44334.155527459 2× π ×7056 2 312821801.40175
Число 7056 в других системах счисления
Римское написание
Двоичная система счисления
Шестнадцатеричная система счисления
Восьмеричная система счисления
Как пишется число 7056 на других языках
На английском языке
seven thousand fifty-six
по цифрам: seven zero five six
На испанском языке
siete mil cincuenta y seis
по цифрам: siete cero cinco seis
На итальянском языке
sette mila cinquantasei
по цифрам: sette zero cinque sei
На немецком языке
sieben tausend sechsundfünfzig
по цифрам: sieben null fünf sechs
На французском языке
sept mille cinquante-six
по цифрам: sept zero cinq six
На португальском языке
sete mil e cinqüenta e seis
по цифрам: sete zero cinco seis
На китайском языке
七千零五十六
по цифрам: 七 零 五 六
На русском языке
семь тысяч пятьдесят шесть
по цифрам: семь ноль пять шесть
На латыни
по цифрам: septem nihil quinque sex
Конвертация времени, длины, веса, скорости и температуры
Конвертация времени
7056 миллисекунд (мс) это 7.056 секунд (с), 0.118 минут (мин), 0.002 часов (ч).
7056 секунд (с) это 7056000 миллисекунд (мс), 117.6 минут (мин), 1.96 час (ч), 0.082 дней.
7056 минут (мин) это 423360 секунд (с), 117.6 часов (ч), 4.9 дня, 0.7 недель, 0.163 месяцев.
7056 часов (ч) это 25401600 секунд (с), 423360 минут (мин), 294 дня, 42 недели, 9.8 месяцев, 0.805 лет.
7056 дней это 609638400 секунд (с), 10160640 минут (мин), 169344 часа (ч), 1008 недель, 235.2 месяцев, 19.332 лет.
7056 недель это 71124480 минут (мин), 1185408 часов (ч), 49392 дня, 1646.4 месяцев, 135.692 лет.
7056 месяцев это 304819200 минут (мин), 5080320 часов (ч), 211680 дней, 30340.8 недель, 588 лет.
7056 лет это 3708633600 минут (мин), 61810560 часов (ч), 2575440 дней, 366912 недель, 84672 месяца.
Конвертация длины и расстояния
7056 миллиметров (мм) это 705.6 сантиметров (см), 7.056 метров (м), 0.007 километров (км); 277.795 дюймов, 23.15 фута, 7.717 ярдов, 0.004 миль, 0.004 морских миль.
7056 сантиметров (см) это 70560 миллиметров (мм), 70.56 метров (м), 0.071 километров (км); 2777.953 дюймов, 231.496 фут, 77.165 ярдов, 0.044 миль, 0.038 морских миль.
7056 метров (м) это 7056000 миллиметров (мм), 705600 сантиметров (см), 7.056 километров (км); 277794.72 дюйма, 23150.736 футов, 7719.264 ярдов, 4.384 мили, 3.81 морские мили.
7056 километров (км) это 7056000000 миллиметров (мм), 705600000 сантиметров (см), 7056000 метров (м); 277795277.424 дюймов, 23149607.04 футов, 7716533.328 ярда, 4385.333 миль, 3809.935 морских миль.
7056 дюймов это 179222.4 миллиметра (мм), 17922.24 сантиметра (см), 179.223 метров (м), 0.179 километров (км); 588 футов, 196 ярдов, 0.111 миль, 0.097 морских миль.
7056 футов это 2150668.8 миллиметров (мм), 215066.88 сантиметров (см), 2150.564 метров (м), 2.151 километра (км); 84672 дюйма, 2352 ярда, 1.336 миля, 1.161 морская миля.
7056 ярдов это 6452006.4 миллиметров (мм), 645200.64 сантиметров (см), 6449.726 метров (м), 6.452 километров (км); 254016 дюймов, 21168 футов, 4.009 мили, 3.484 морские мили.
7056 миль это 11355531264 миллиметра (мм), 1135553126.4 сантиметров (см), 11355531.264 метр (м), 11353.104 километра (км); 447068160 дюймов, 37255680 футов, 12418560 ярдов, 6130.321 морских миль.
7056 морских миль это 13067712000 миллиметров (мм), 1306771200 сантиметров (см), 13067712 метров (м), 13067.712 километров (км); 514476851.616 дюйм, 42873067.44 футов, 14291024.832 ярда, 8121.456 миля.
Конвертация веса и массы
7056 миллиграммов (мг) это 35.28 карат (кар), 7.056 граммов (г), 0.007 килограммов (кг), 0.249 унций, 0.016 фунтов.
7056 граммов (г) это 7056000 миллиграммов (мг), 35280 карат (кар), 7.056 килограммов (кг), 248.889 унций, 15.556 фунтов.
7056 карат (кар) это 1411200 миллиграммов (мг), 1411.2 граммов (г), 1.411 килограмм (кг), 49.778 унций, 3.111 фунта.
7056 килограммов (кг) это 7056000000 миллиграммов (мг), 35280000 карат (кар), 7056000 граммов (г), 248893.344 унции, 15558.48 фунтов.
7056 унций это 200034234.288 миллиграмма (мг), 994896 карат (кар), 200037.6 граммов (г), 200.034 килограммов (кг), 441 фунт.
7056 фунтов это 3200547762.72 миллиграмма (мг), 16002739.872 карат (кар), 3200545.152 граммов (г), 3200 килограммов (кг), 112896 унций.
Конвертация скорости движения
7056 километров/час (км/ч) это 1960 метров/секунду (м/с), 4385.333 миль/час, 3809.935 узлов (уз).
7056 метров/секунду (м/с) это 25401.6 километр/час (км/ч), 15784.272 мили/час, 13716.864 узлов (уз).
7056 миль/час это 11353.104 километра/час (км/ч), 3154.224 метра/секунду (м/с), 6130.321 узлов (уз).
7056 узлов (уз) это 13067.712 километров/час (км/ч), 3629.63 метров/секунду (м/с), 8121.456 миля/час.
Конвертация температуры
7056 градусов по Цельсию (°C) это 12732.8 градуса по Фаренгейту (°F) и 7329.15 градусов по Кельвину (K).
7056 градусов по Фаренгейту (°F) это 3902.22 градуса по Цельсию (°C) и 4175.37 градусов по Кельвину (K).
7056 градусов по Кельвину (K) это 6782.85 градуса по Цельсию (°C) и 12241.13 градус по Фаренгейту (°F).
Информация о числах
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители.
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел.
Сейчас изучают числа:
Число 7056
Семь тысяч пятьдесят шесть
RGB(0, 27, 144) или #001B90
(возможное основание)
доброжелательность, благородство, прощение, раскаяние, благодарность, исцеление, щедрость, великодушие
Описание числа 7056
Вычислить квадратный корень из числа

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
| Число знаков после запятой: |
| √ |
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
25, 36, 49 — квадратные числа, поскольку:
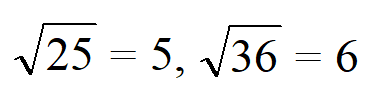
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 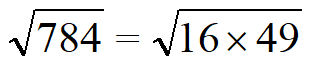 |
| Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 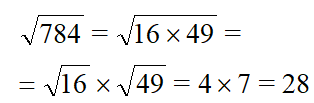 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 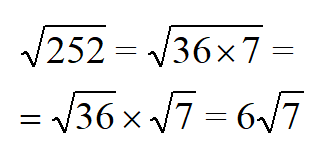 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76 7. |
| Вычисляем корень | 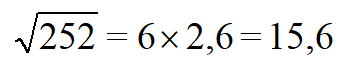 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. |  |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 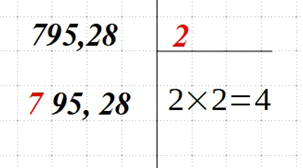 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 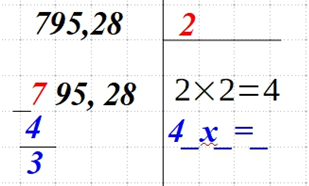 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 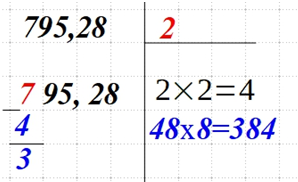 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 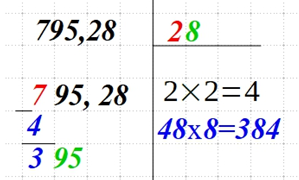 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 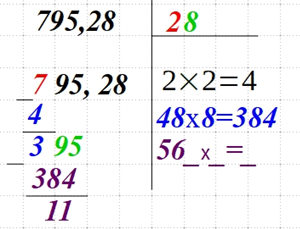 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 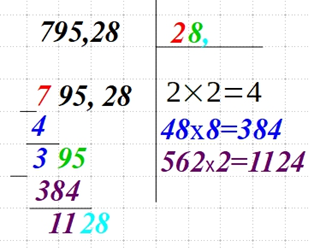 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 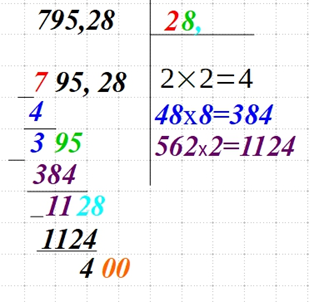 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни. Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
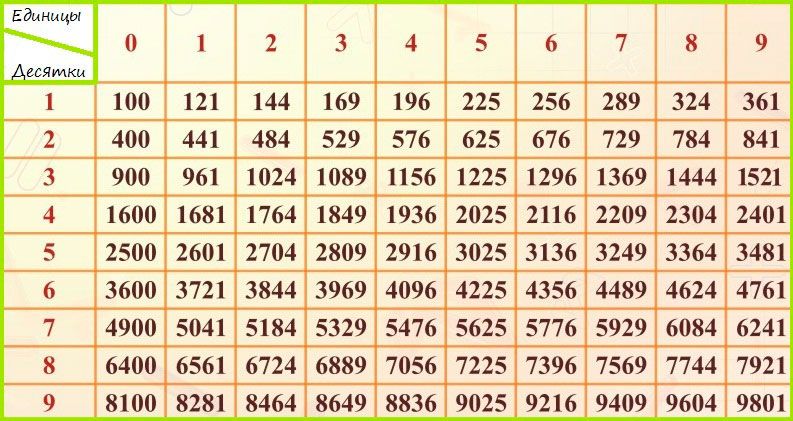
Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9. Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.
Внесение под знак корня
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 2 2 х3 и 3 2 х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные. Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто.

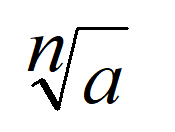
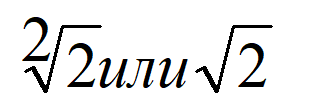
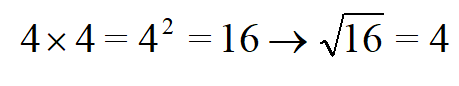
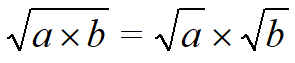
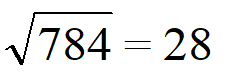
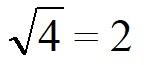
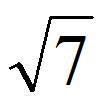 между 2 и 4.
между 2 и 4.