Критерий архимеда в чем измеряется

Число Архимеда

Механика сплошных сред

Сплошная среда

Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

См. также: Портал:Физика

Число Архимеда [1] () — названная в честь древнегреческого учёного Архимеда, безразмерная величина, используется при нахождении движения жидкости, возникающего из-за неоднородностей её плотности:

где — ускорение свободного падения (9,81 м/с²);

— плотность жидкости, кг/м³;

— плотность тела, кг/м³;

— динамическая вязкость, Па·с;

— кинематическая вязкость;

— определяющий линейный размер тела, м.

Примечания

Безразмерные величины в физике
Понятия	Размерность физической величины · Безразмерная величина · π-Теорема · Критерий подобия
Числа	Аббе · Альфвена · Архимеда · Атвуда · Багнольда · Био · Бонда · Бринкмана · Булыгина · Вебера · Вайсенберга · Галилея · Гартмана · Гей-Люссака · Грасгофа · Гретца · Гуше · Дамкёлера · Деборы · Дерягина · Дина · капиллярности · Кармана · Каулинга · Кирпичёва · Клаузиуса · Кнудсена · Коссовича · Коши · Лапласа · Лундквиста · Лыкова · Льюиса · Лященко · Маха · Марангони · Мортона · Нуссельта · Ньютона · Онезорге · Пекле · Поснова · Прандтля (магнитное, турбулентное) · Пуазёйля · Рейнольдса (магнитное) · Ричардсона · Россби · Роуза · Рошко · Руарка · Рэлея · Соре · Стэнтона · Стокса · Струхаля · Стюарта · Суратмана · Тейлора · Уомерсли · Фёдорова (в гидродинамике · в теории сушки) · Фруда · Фурье · Хагена · Чандрасекара · Шмидта · Шервуда · Эйлера · Эккерта · Экмана · Элсассера · Этвёша

Полезное

Смотреть что такое «Число Архимеда» в других словарях:

число Архимеда — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN Archimedes numberAr … Справочник технического переводчика

Число Бонда — ( или ) критерий подобия в гидродинамике, определяющий соотношение между внешними силами (обычно силой тяжести) и силами поверхностного натяжения. Оно выражается следующим образом: где коэффициент поверхностного натяжения жидкости 2; … Википедия

Число Этвёша — (Eo) критерий подобия в гидродинамике, определяющий соотношение между внешними силами (обычно силой тяжести) и силами поверхностного натяжения. Оно выражается следующим образом: где σ коэффициент поверхностного натяжения жидкости 2;… … Википедия

Число Ричардсона — ( ) критерий подобия в гидродинамике, равный отношению потенциальной энергии тела, погружённого в жидкость к его кинетической энергии. Под «телом» здесь обычно понимается рассматриваемая жидкость или газ. В общем случае число Ричардсона… … Википедия

АРХИМЕДА ЧИСЛО — подобия критерий двух гидродинамич. или тепловых явлений, при к рых определяющими явл. выталкивающая (архимедова) сила (см. АРХИМЕДА ЗАКОН) и сила вязкости. где l характерный линейный размер, v коэфф. кинематич. вязкости, r и r1 плотность среды в … Физическая энциклопедия

Число (матем.) — Число, важнейшее математическое понятие. Возникнув в простейшем виде ещё в первобытном обществе, понятие Ч. изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности и связанного с ним… … Большая советская энциклопедия

Число Лященко — ( ) критерий подобия в гидродинамике, выражающий соотношение сил инерции, тяжести и подъёмной силы. Оно определяется следующим образом: где: плотность; динамическая вязкость; ускорение свободного п … Википедия

Число Мортона — (Mo) критерий подобия в гидродинамике, которое наряду с числом Этвёша характеризует форму пузырей и капель, движущихся внутри жидкости. где ускорение свободного падения; динамическая вязкость; плотность окружающей… … Википедия

Архимеда число — характеризует собой соотношение между архимедовой силой, обусловленной различием плотностей в отдельных областях рассматриваемой системы, и вязкими силами в основном потоке. Используется в качестве параметра подобия при анализе задач по… … Энциклопедия техники

Источник

Архимедова сила

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сила: что это за величина

Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.

В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.

Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Открытие закона Архимеда

Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.

Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.

Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.

Формула плотности тела

ρ = m/V

ρ — плотность тела [кг/м 3 ]

m — масса тела [кг]

V — объем тела [м 3 ]

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻‍♂️

Формула и определение силы Архимеда для жидкости

На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.

Определение архимедовой силы для жидкостей звучит так:

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

Формула архимедовой силы для жидкости

ρ_ж — плотность жидкости[кг/м 3 ]

V_погр — объем погруженной части тела [м 3 ]

g — ускорение свободного падения [м/с 2 ]

А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.

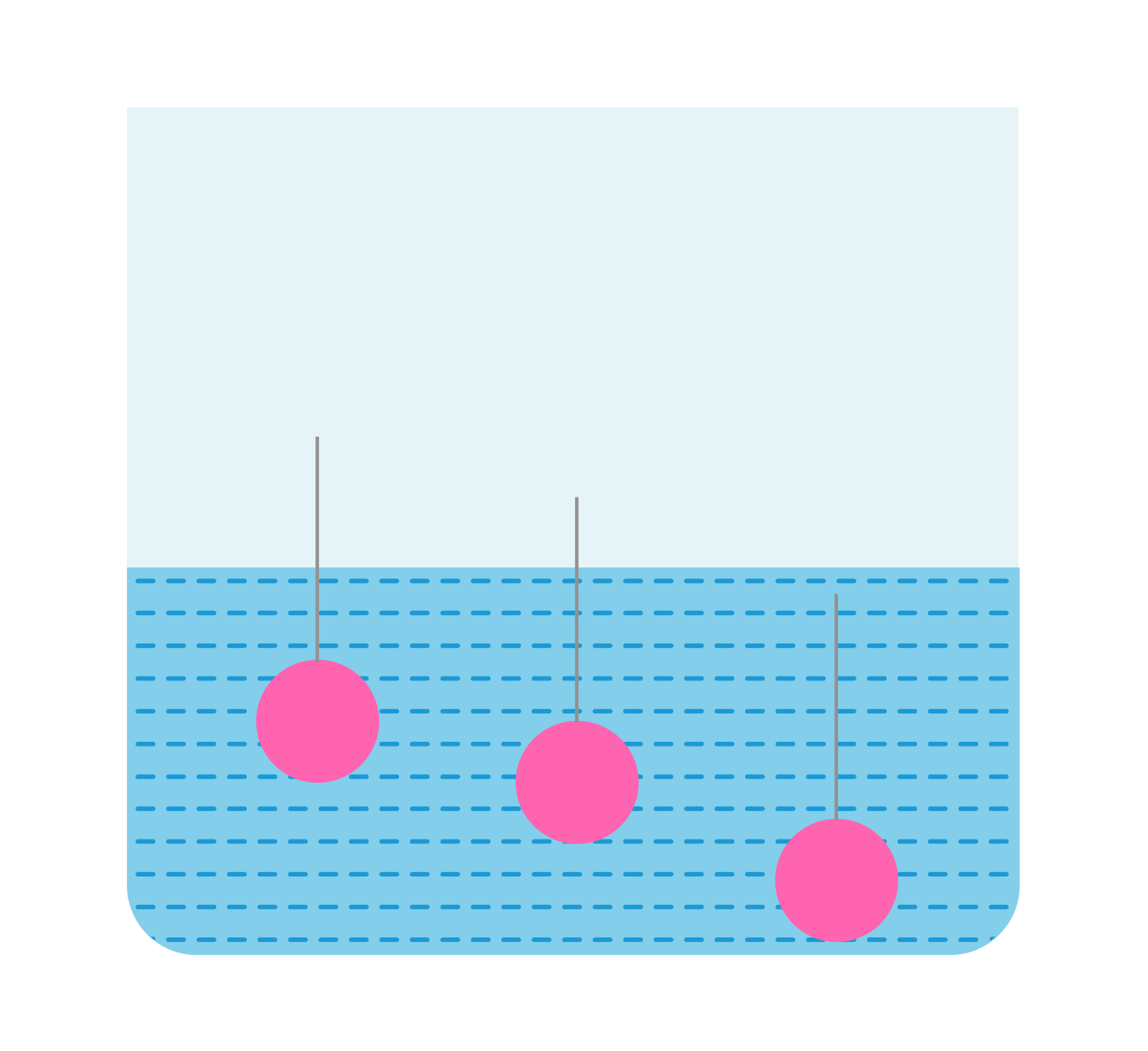
Задача 1

В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.

Решение

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

Задача 2

Решение

Сила Архимеда, действующая на кубик, равна F_Арх = ρ_жgV_погр.

V_погр. — объем погруженной части кубика,

ρ_ж — плотность жидкости.

Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:

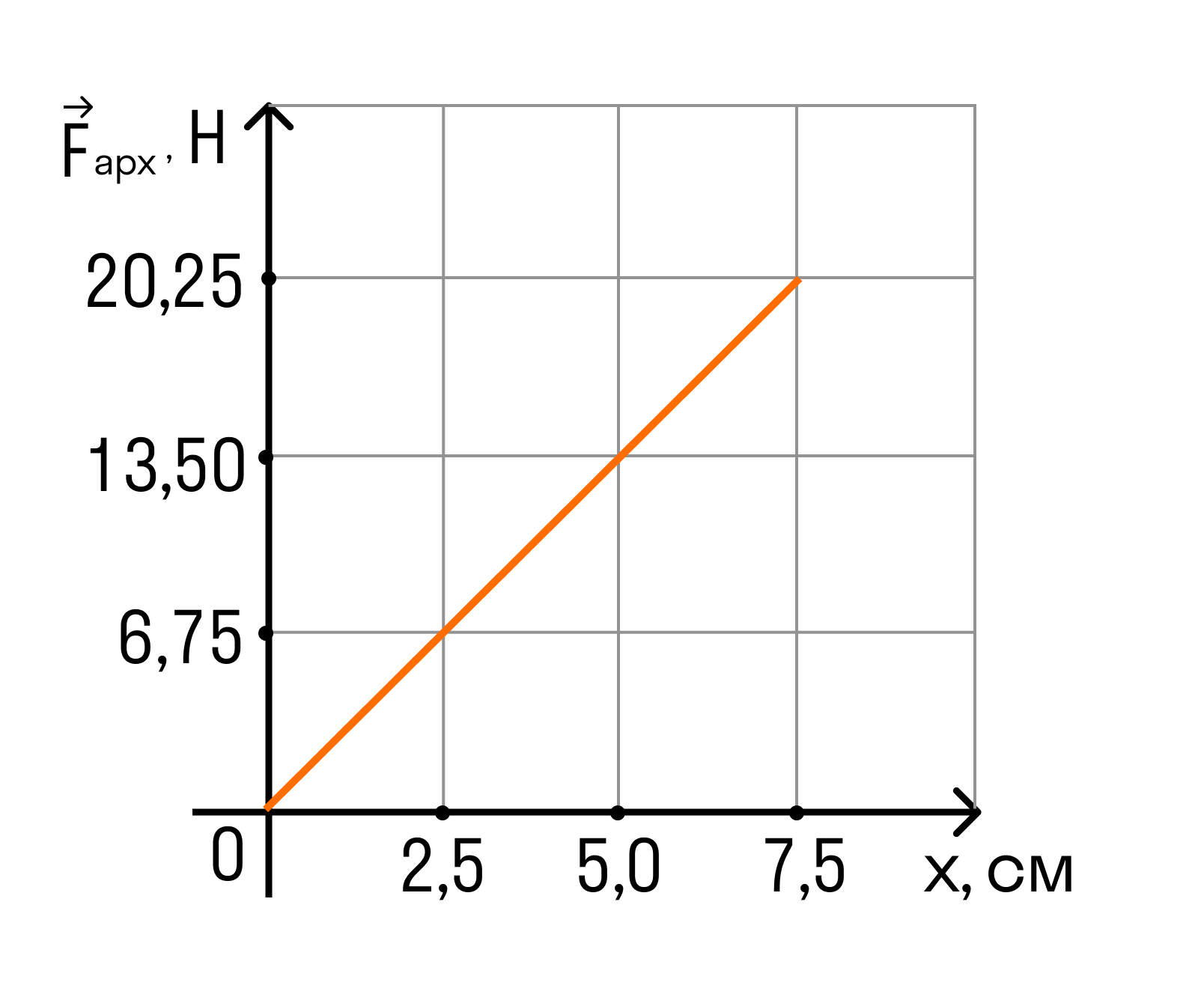
где а — длина стороны кубика.

Рассматривая любую точку данного графика, получим:

Условия плавания тел

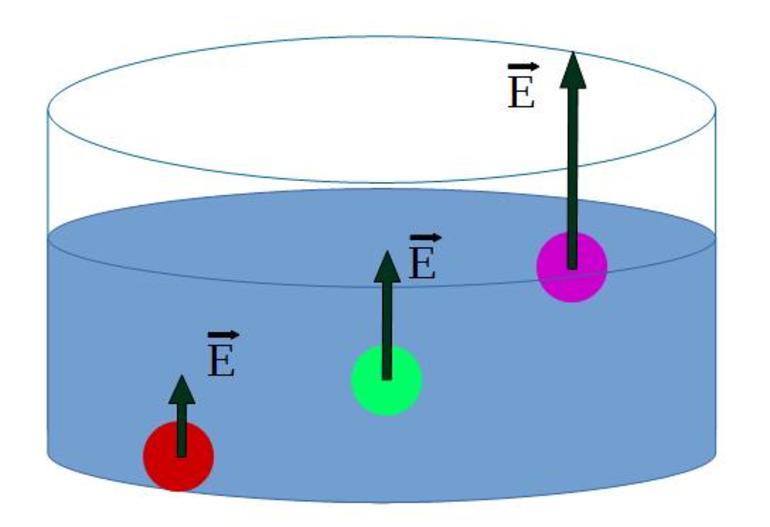
Из закона Архимеда вытекают следствия об условиях плавания тел.

Погружение

Плавание внутри жидкости

Плавание на поверхности жидкости

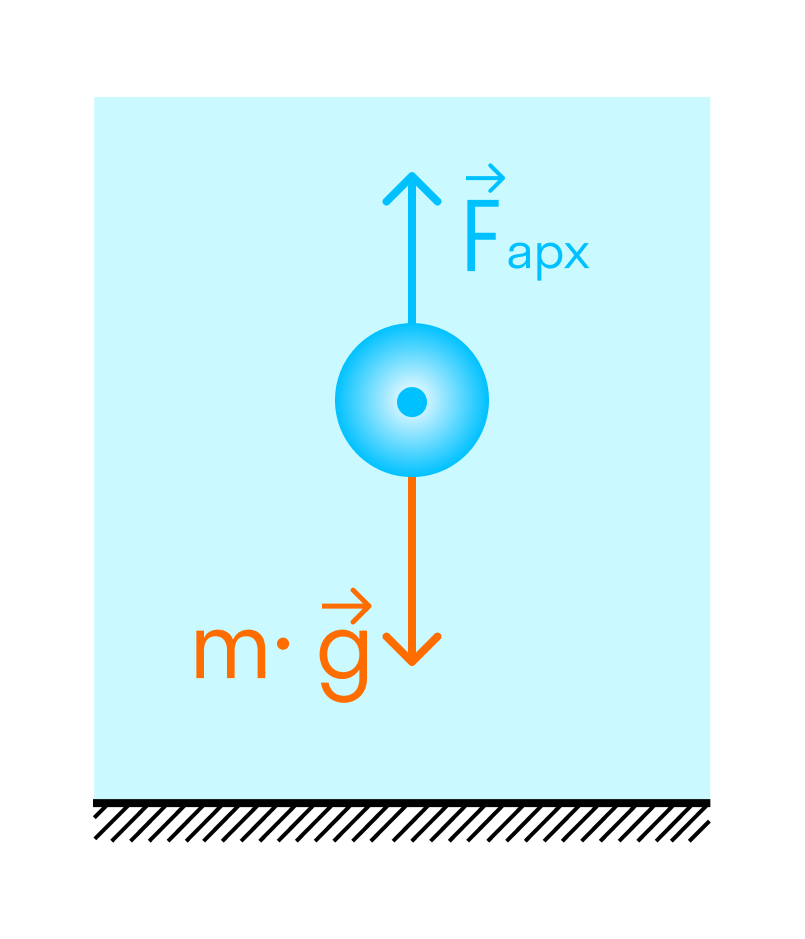
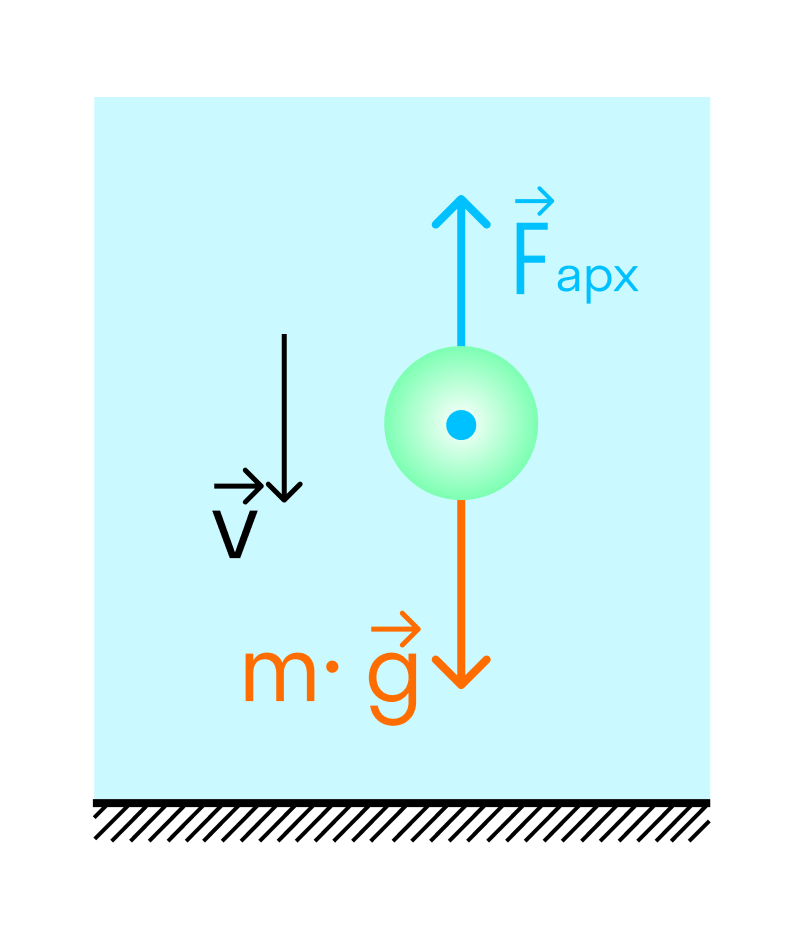
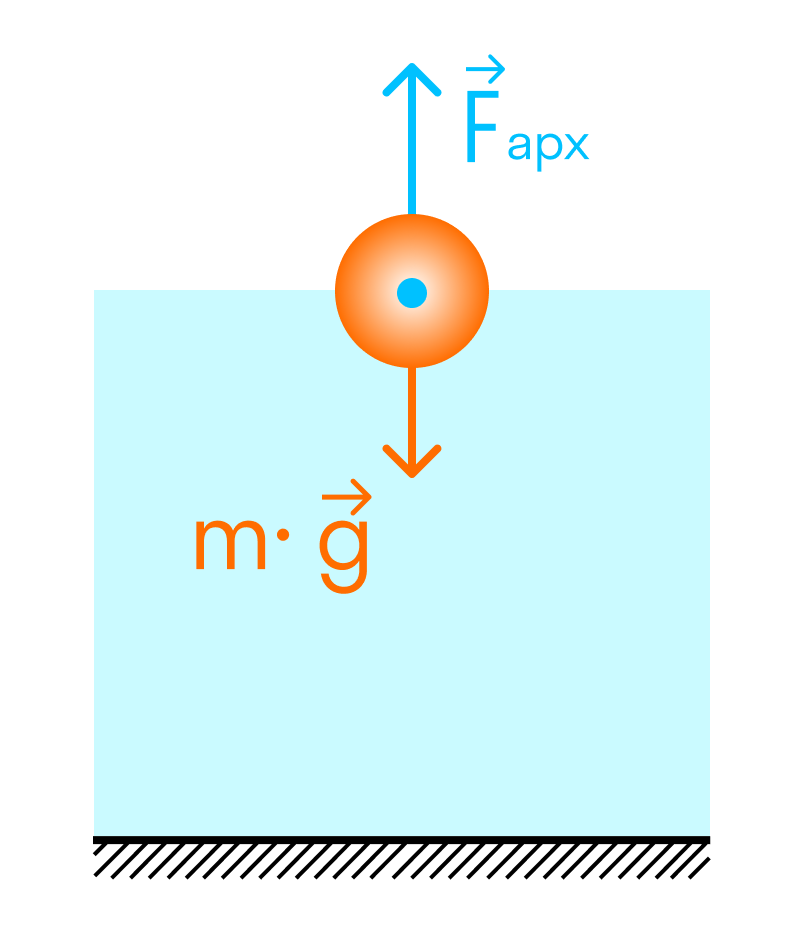
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.

Почему корабли не тонут?

Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.

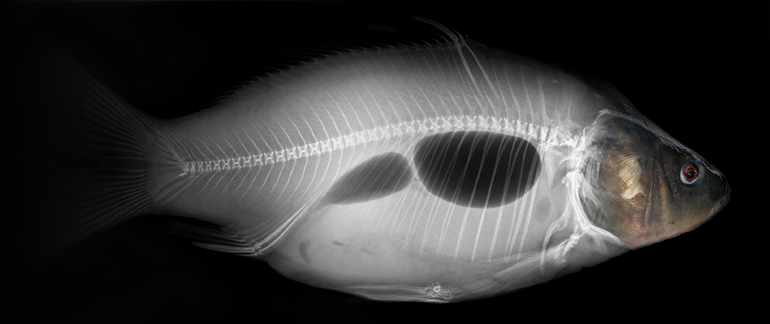
В подводных лодках есть специальные резервуары, которые заполняют водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.

Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.

Формула и определение силы Архимеда для газов

На самом деле тут все очень похоже на жидкости. Начнем с формулировки закона Архимеда:

Выталкивающая сила, действующая на тело, погруженное в газ, равна по модулю весу вытесненного газа и противоположно ему направлена.

Формула архимедовой силы для газов

ρ_г — плотность газа [кг/м 3 ]

V_погр — объем погруженной части тела [м 3 ]

g — ускорение свободного падения [м/с 2 ]

Сила Архимеда для газов действует аналогично архимедовой силе для жидкостей. Давайте убедимся в этом, решив задачку.

Задача

Решение

Подставляем значения и получаем:

По второму закону Ньютона для инерциальных систем отсчета:

Выражаем массу груза и подставляем значения:

m = F_Арх / g = 0,39 / 10 = 0, 039 кг = 39 кг

Ответ: груз максимальной массы 39 г может удержать данный шарик с гелием.

Когда сила Архимеда не работает

Архимедова сила не работает лишь в трех случаях:

Невесомость. Главное условие возникновения Архимедовой силы — это наличие веса у среды. Если мы находимся в невесомости, холодный воздух не опускается, а горячий, наоборот, не поднимается.

Тело плотно прилегает к поверхности. Отсутствие газа или жидкости между поверхностью и телом свидетельствует об отсутствии выталкивающей силы — телу просто неоткуда выталкиваться.

Растворы и смеси. Если взять спирт, плотность которого меньше плотности воды, и смешать его с водой, получится раствор. На него не будет действовать сила Архимеда, несмотря на то, что плотность спирта меньше плотности воды — он просто растворится.

Источник

Определение и формула

Закон Архимеда гласит, что если твёрдое тело погружено в жидкость, то на него действует выталкивающая сила, равная весу жидкости в объёме тела.

При некоторых обстоятельствах объём вещества одинаков объёму воды. В частности, когда твёрдый объект любого класса полностью погружен в воду, объём вытесненной воды должен быть равен объёму объекта. Кроме того, по определению силы Архимеда, при погружении объект получит плавучую силу, одинаковую весу вытесненной воды. Таким образом, объект, взвешенный в воздухе и затем взвешенный при погружении в воду, будет иметь эффективный вес, уменьшенный на вес вытесненной воды, если подъёмная сила воздуха незначительна.

Что произойдёт, если стакан наполнить водой доверху, а затем добавить кубики льда? Точно так же, как вода расплескалась через край, когда Архимед сел в свою ванну, жидкость в стакане выльется, если бросить туда кубики льда. Если взвесить разлившуюся воду (вес — это сила, направленная вниз), она будет равняться восходящей силе на предмете. По этой силе можно определить объём или среднюю плотность объекта.

При взвешивании в воздухе предмет получает силу выталкивания, равную весу воздуха, перемещаемого объектом. Однако плотность воздуха довольно мала (по сравнению с плотностью большинства твёрдых частиц), чтобы можно было пренебречь этой плавучей силой при взвешивании большинства твёрдых частиц в воздухе.

Формула силы Архимеда записывается как F = pgV, где:

Формула принципа Архимеда полезна для нахождения силы, объёма смещённого тела или плотности жидкости, при условии, что некоторые из этих чисел известны.

При демонстрации закона Архимеда следует отметить, что в этом явлении многое зависит от гравитации. То есть сила плавучести, которая всегда противостоит элементу притяжения, на самом деле вызвана самой гравитацией. Давление внутри флюидов вырастает с увеличением глубины, поскольку внутри жидкости действует гравитационный вес сверху. Это давление, которое постоянно повышается, прикладывает силу к объекту, погруженному в воду, и увеличивается с глубиной жидкости. Результатом этого является плавучесть.

Принцип плавучести

Принцип Архимеда показывает подъёмную силу и вытеснение жидкости. Однако эта концепция может быть применена при рассмотрении вопроса плавания предметов. Пятый трактат Архимеда «О плавающих телах» гласит, что любой плавающий объект вытесняет собственный вес жидкости.

Другими словами, для предмета, плавающего на поверхности жидкости (например, лодки) или плавающего под водой (субмарина или дирижабль в воздухе), вес вытесненной жидкости равен весу объекта. Таким образом, только в особом случае плавания сила выталкивания, действующая на объект, равна его весу.

Например, существует блок из твёрдого железа, который весит 1 тонну. Поскольку железо почти в восемь раз плотнее воды, при погружении оно вытесняет только 1/8 тонны воды, что недостаточно для удержания его на плаву. Теперь следует предположить, что тот же железный блок преобразован в чашу. Он по-прежнему весит 1 тонну, но при помещении в жидкость он вытесняет больший объём воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем сильнее действует на неё выталкивающая сила. Когда плавучая сила равна 1 тонне, она не опустится дальше.

Когда лодка вытесняет вес воды, равный её собственному весу, она плавает. Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы смещать вес жидкости, по крайней мере, равный его собственному весу. Корпус 10000-тонного корабля должен быть достаточно широким, длинным и глубоким, чтобы вытеснять соответствующее количество тонн воды. Он нуждается в дополнительной грани для равновесия и борьбы с волнами, которые иначе заполнили бы его и, увеличив его массу, потопили корабль.

Практически принцип Архимеда позволяет рассчитывать плавучесть объекта, частично или полностью погруженного в жидкость:

Следует отметить, что если вес объекта меньше, чем вес вытесняемой жидкости, объект будет испытывать подъём, как и происходит в случае с деревянным брусом, который остаётся ниже поверхности воды. Объект, который по своей природе тяжелее количества жидкости, которую он может вытеснить, утонет при освобождении, но в то же время испытает потерю веса, равную весу вытесненной жидкости. Фактически, когда дело доходит до взвешивания, необходимо внести поправку, чтобы иметь возможность компенсировать эффект плавучести окружающего его воздуха.

Хотя они связаны с этим, принцип плавания и концепция, согласно которой затопленный объект вытесняет объём жидкости, равный его собственному объёму, не являются законом Архимеда. Как указано выше, он приравнивает подъёмную силу к весу вытесненной жидкости.

Практическое применение

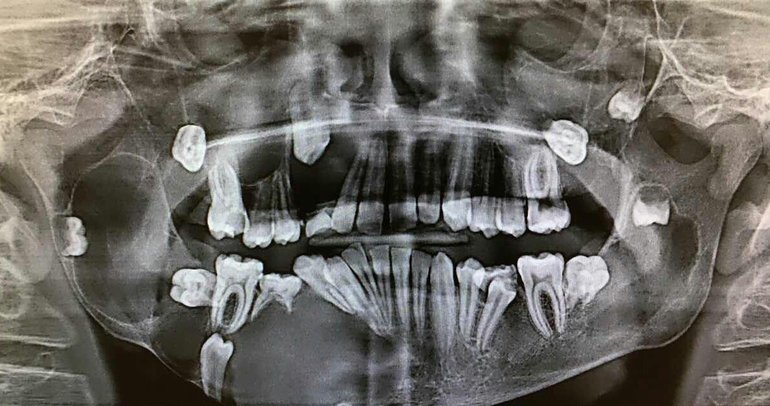
Принцип Архимеда имеет множество применений в области медицины и стоматологии и используется для определения плотности костей и зубов. В статье 1997 года, опубликованной в журнале Medical Engineering & Physics, исследователи использовали силу Архимеда для измерения объёма внутренней губчатой ​​части кости, которая может применяться в различных исследованиях старения, остеопороза, прочности костей, жёсткости и эластичности.

В статье, опубликованной в 2017 году в журнале Oral Surgery, использовались различные методы для определения воспроизводимости, одним из которых был принцип Архимеда. Его сравнивали с использованием конусно-лучевой компьютерной томографии для измерения объёма зубов. Тесты, сравнивающие закон и замера КЛКТ, показали, что последние будут точным инструментом при планировании стоматологических процедур.

Простой, надёжный и экономически эффективный проект для подводной лодки, описанный в статье 2014 года в журнале Informatics, Electronics and Vision, основан на принципе Архимеда. Конструкция этой прототипной субмарины использует расчёты, включающие массу, плотность и объём как подводной лодки, так и вытесненной воды, чтобы определить необходимый размер балластного танка. Он должен обозначить количество воды, способное его заполнить, и, следовательно, выяснить нижнюю границу глубины, на которую может погружаться подводная лодка.

Также можно наблюдать действие силы Архимеда в природе:

Греческий учёный внёс огромный вклад в кораблестроение, сформировав критерии устойчивости плавающих объектов. Закон Архимеда также используется в широком спектре научных исследований, включая медицину, инженерию, энтомологию, инженерию и геологию.

Открытие закона

По легенде, некоторым своим современникам Архимед запомнился как человек, который бегал голым по улицам Сиракуз с криками «Эврика!», что в переводе означает «Нашёл!». Причиной возникновения этого события являлось данное Архимеду поручение доказать, что новая корона, сделанная для царя, не была из сплошного золота, как утверждал ювелир. Архимед долго работал над этой задачей, но никак не мог найти способ доказать недобросовестность изготовителя. Тем не менее проницательность грека привела к решению проблемы, поставленной перед ним Гиероном II.

Однажды Архимед наполнил ванну и заметил, что вода пролилась через край, когда он сел в неё. Тогда учёный понял, что жидкость, вытесненная его телом, была равна его весу. Оборудование для взвешивания объектов с достаточной точностью уже существовало, и теперь, когда Архимед также мог измерить объём, их соотношение дало бы плотность объекта — важный показатель чистоты, поскольку золото почти в два раза плотнее серебра и имеет значительно больший вес для того же объёма вещества при стандартных температурах и давлении.

Итак, зная, что золото тяжелее других металлов, которые мог бы использовать изготовитель короны, Архимед определил, что украшение не отличалось чистотой материала. Забыв о своей наготе, он побежал по улицам от дома к царю, крича: «Эврика!»

Источник

«Не трогай моих кругов» – число Пи и гибель Архимеда

Продолжаю исторические посты-коротыши, сегодня – об Архимеде. Но перед этим небольшое вступление о событиях куда более недавних, чтобы было понятно, почему этот пост размещаю именно сегодня.

В 1988 году американский физик Ларри Шоу заметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 совпадает с числом π и предложил учредить к этой дате математический праздник – День числа π.

Праздник быстро стал популярным и в 2006 году Конгресс США включил его в официальный список американских праздников, а спустя несколько лет решением ЮНЕСКО за ним закрепили международный статус. Ну а в этом году у числа π еще и свой юбилей – 314 лет с того времени, как его придумали. В 1706 году британский математик Уильям Джонс впервые предложил греческую букву π для обозначения отношения длины окружности к её диаметру (поскольку эта буква начальная в греческих словах περιφέρεια — окружность, периферия и περίμετρος — периметр).

Важный момент, Джонс придумал наименование, сама эта величина была известна достаточно давно, просто под более длинным наименованием «величина, равная отношению длины окружности к её диаметру» и т.п.

Ее вычислением занимались тысячелетия назад, еще в Древнем Египте, есть также легенда, что эту постоянную использовали при проектировании Вавилонской башни. Внес свой вклад в ее расчеты известный древнегреческий математик, физик и инженер Архимед.

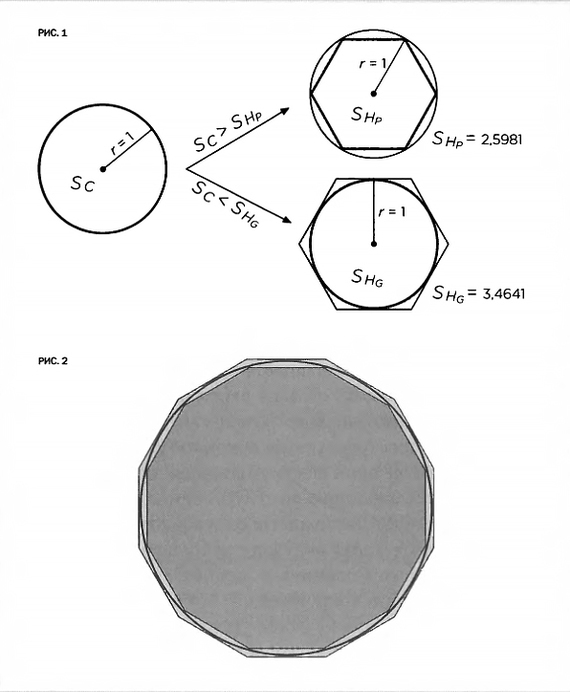
В те времена перед античными математиками встала проблема – как вычислять площадь криволинейных фигур, кругов, овалов и т.п. Частично решить ее удалось с помощью метода исчерпывания (впервые его применил Евклид, а Архимед взял на вооружение и усовершенствовал).

Чтобы его использовать, надо вписать один многоугольник в окружность, а другой описать вокруг нее, тем самым зажав ее между ними. Площадь многоугольников вычислять греки умели, значение площади окружности располагалось где-то в интервале между большим и меньшим многоугольником. Причем, чем больше было сторон у многоугольников, тем меньше был интервал, а следовательно – точнее был результат вычисления площади окружности. И первым эту идею выдвинул как раз Архимед, для начала заменив шестиугольник (который использовали до него) на двенадцатиугольник.

Далее он продолжил увеличивать число сторон и дошел до фигуры с 96 углами. В итоге, была сформулирована т.н. «аксиома Архимеда» о том, что можно найти настолько близкий к площади криволинейной фигуры многоугольник, насколько пожелаешь, но при этом точного результата все равно не достигнешь. Ограничением, по сути, служили цели вычислений, для хозяйственных нужд можно было округлять сильнее, а для научных трактатов – вычислять с максимально возможной точностью. Сам Архимед рассчитал, что соотношение длины окружности и диаметра равно 3( 10)⁄71, он также доказал, что площадь круга равна числу этого соотношения, умноженному на квадрат радиуса круга.

В дальнейшем Архимед еще не раз возвращался к вычислениям методом исчерпывания, стремясь достичь еще большей точности. По легенде, изложенной Плутархом, именно этим ученый занимался и тогда, когда римские войска ворвались в его родной город Сиракузы (хотя немало времени он уделял и вопросам обороны города, но это уже другая история). Он так увлекся, что даже не заметил ворвавшихся солдат. Неожиданно перед ним возник легионер, который потребовал от Архимеда явиться к Марцеллу (командующему римским войском). Погруженный в задачу, Архимед лишь отмахнулся от него – «Не трогай моих кругов», легионер же, офигев от такого отношения, не нашел ничего лучше, как зарубить ученого. Правда, Марцелл за это легионера наказал, поскольку хотел именно пленить Архимеда, которого называл «Бриареем среди геометров».

Свой метод Архимед применял и к объемным фигурам, вычислив соотношение площадей поверхности цилиндра и вписанного в него шара. С этим связана еще одна легенда, что Архимед завещал выбить изображение шара, вписанного в цилиндр на своем надгробии вместо эпитафии. Впрочем, Цицерон утверждал, что своими глазами видел это надгробие, так что, возможно, это не такая уж легенда.

Лига историков

8.3K поста 36K подписчиков

Правила сообщества

— уважение к читателю и открытость

— регулярность и качество публикаций

— умение учить и учиться

— бездумный конвейер копипасты

— публикации на неисторическую тему / недостоверной исторической информации

— простановка тега [моё] на компиляционных постах

— неполные посты со ссылками на сторонний ресурс / рекламные посты

— видео без текстового сопровождения/конспекта (кроме лекций от профессионалов)

— дискуссии на тему постов

— уважение к труду автора

— личные оскорбления и провокации

— неподкрепленные фактами утверждения

Студенты-биологи на полевой практике. Тема: устройство муравейника. После множества обмеров пришли к выводу, что соотношение периметра муравейника в его диаметру примерно равно 3. Этот факт был подан в отчете о практике, почти как научное открытие.

Мне это историю рассказывали как реальную.

Хороший мультик в тему.

Почему пост так поздно появился? 🙁

Вчера надо было этот большой праздник отмечать и ПИть шампанское.

3( 10)⁄71-это скобка порченая, или буква?

Как Пифагор «придумал» музыку и музыку ли он придумал? 😉 Как возникла современная музыкальная система и как в её звуки связаны между собой? Почему нот семь, а на фортепиано семь белых и пять черных клавиш? Где об этом можно прочитать подробнее?

Число Пи

Великий механик: пять коротких историй из жизни Архимеда

История первая. Как взвесить корону

Эту историю все знают из школьных учебников. Правитель Сиракуз (города на Сицилии, где, собственно, и жил Архимед) Гиерон заподозрил, что ювелир, изготовивший ему новую корону, украл часть золота, заменив его серебром. И попросил Архимеда внести ясность в этот вопрос, не разрушая саму корону. Согласно легенде, мудрец долго искал способ как измерить плотность материала короны и в результате, открыл свой знаменитый закон: каждое тело, погруженное в жидкость, теряет столько своего веса, сколько весит вытесненная им жидкость.

Я тоже помню эту историю по школе. Но как мы, школьники, представляли себе процесс экспертизы короны. Архимед ставит сосуд, наполненный водой до краев, в таз, потом погружает в сосуд корону и замеряет, сколько воды вылилось, узнав тем самым ее объем. Потом взвесил корону, узнал ее массу. Поделил массу на объем вылитой воды, узнал плотность материала, сравнил с плотностью золота… Вопросом, откуда Архимед знал значение плотности золота в школе я не задавался.

Уже позже я услышал совсем другое описание этого эксперимента. Архимед взял рычажные весы, на один конец поместил корону, на другую некий вес, равный ей (например, песок). Потом поднес снизу к короне полное ведро воды и погрузил ее в ведро, не отцепляя от весов. Корона, понятно, потеряла часть своего веса и, чтобы снова уравновесить планку, груз надо было передвинуть ближе к центру весов. Замерив расстояние, на которое пришлось сдвигать противовес, Архимед повторил опыт с куском чистого золота, равным тому, что выдали ювелиру. Иначе говоря, Архимед придумал простой, но действенный способ сравнения плотностей разных веществ.

Легенда гласит, что опыт разоблачил жульничество ювелира, потому что противовес пришлось сдвигать иначе. Впрочем, это имело значение для Гиерона, а для науки, конечно, важнее сам принцип, который стал основным законом гидростатики.

История вторая. Как перевернуть корабль

Сам рычаг был известен человечеству задолго до Архимеда (например, строителям египетских пирамид). Но именно Архимед сформулировал первую механико-математическую теорию рычага в трактате «О равновесии плоских фигур» и успешно применял ее на практике, создавая довольно сложные рычажные конструкции.

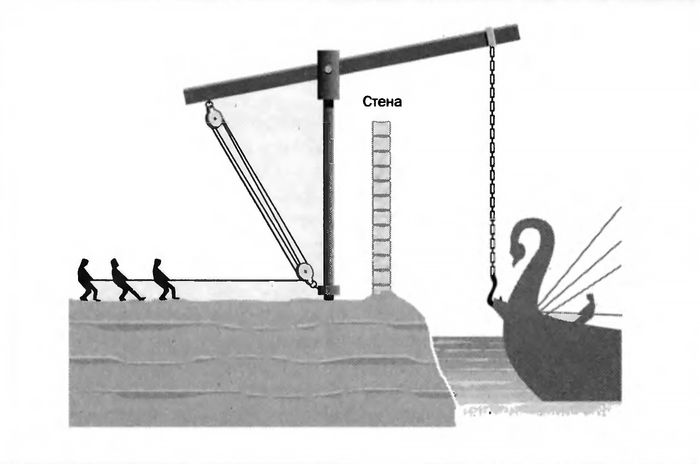
Когда по приказу все того же Гиерона был построен тяжелый многопалубный корабль «Сиракузия» (считается, что он весил более полутора тысяч тонн), встала проблема – как спустить его на воду, не разломав при этом. Понятно дело, снова привлекли Архимеда. В итоге, мудрец соорудил грузоподъёмное устройство, состоящее из собранных в подвижную и неподвижную обоймы блоков, последовательно огибаемых канатом – полиспаст.

По легенде, с помощью этого устройства он смог в одиночку приподнять корабль и перетащить его к воде. Тогда, дескать, он и выдал свой знаменитый афоризм.

Так это или нет, но Архимеда принято считать изобретателем этого устройства, которое по сей день широко используется, причем не только для перемещения грузов. Кстати, по другой легенде, когда римляне осадили Сиракузы, полиспастам нашлось и другое применение: защитники города цепляли крюками борта римских кораблей, приближавшихся к городским стенам и с помощью полиспастов (к которым крепились канаты с крюками) поднимали и переворачивали их. Такие устройства называли «коготь Архимеда».

История третья. Тела небесные

В 1900 году водолазы обнаружили в Эгейском море затонувший античный римский корабль. В течение следующего года с корабля подняли массу артефактов, самый известный получил название Антикитерского механизма. Это устройство и история его изучения заслуживают отдельного поста. Здесь же ограничусь кратким определением: он считается самым древним механическим вычислительным устройством, использовался для расчёта конфигурации движения всех известных в древности планет, включая Марс, Юпитер, Сатурн. Причем тут Архимед? Дело в том, что такое сложное устройство «на пустом месте» не построить, и одним из предшественников его создателей был как раз мудрый грек из Сиракуз.

Астрономия не относилась к главным научным интересам Архимеда. Но он все же написал астрономический трактат «О строении сфер», который, увы, до нас не дошел. Поэтому о его концепции мироустройства мы знаем только со слов других. Архимед в целом был согласен с геоцентрической картиной мира от Аристотеля, где в центре мироздания расположена Земля. Но при этом он считал, что Венера, Марс и Меркурий – обращаются вокруг Солнца и уже вместе с ним – вокруг Земли. В общем система получалась сложная, и чтобы сделать ее более наглядной Архимед (по свидетельству Цицерона) построил механическую модель движения Солнца, Луны, планет и звезд. Модель представляла собой большую металлическую конструкцию и называлась – планетарий.

Причем, они не просто двигались в произвольном порядке, модель Архимеда позволяла рассчитывать фазы Луны и предсказывать даты затмений. По крайней мере, так уверяли очевидцы. После того, как римляне все-таки взяли Сиракузы (Архимед погиб во время штурма), планетарий в числе трофеев увезли в римский храм Доблести. И если одних этот трофей просто развлекал, то других, видимо, подтолкнул к созданию аналогов и даже более сложных вещей, что в итоге и вылилось в создание римлянами Антикитерского механизма. Но это уже исключительно моя версия.

История четвертая. Простые вещи

Когда мы говорим о наследии Архимеда, надо помнить, что оно нас окружает в буквальном смысле слова. Я уже писал, что он написал математическую теорию рычага. Но это не все. Его считают автором теории пяти механизмов, известных в его время и именуемых «простые механизмы». Это – рычаг, наклонная плоскость, блок, лебедка и бесконечный винт. Последний механизм он изобрел и одновременно придумал резьбовое соединение элементов – винта и гайки. А теперь попробуйте представить себе жилье, в котором нет ни одного резьбового соединения. Так что все мы постоянно пользуемся плодами научного наследия Архимеда, даже не подозревая об этом.

История пятая. Математические достижения

Математика была главной наукой в жизни Архимеда. И он добился в этой области потрясающих результатов. О его вычислениях числа π я рассказывал в одном из постов. Есть мнение, что он продолжал эту работу, когда римляне ворвались в Сиракузы и не пожелал прерваться, что и стало причиной его гибели. Но вот сам Архимед считал своим главным математическим достижением – расчет соотношения объемов цилиндра и вписанного в него шара (оно равно 3/2). Это при условии, что диаметр шара равен диаметру основания цилиндра и его высоте. Такое же соотношение и у площадей их поверхностей. Кому-то может показаться, что это не такая уж сложная задача. Но, напомню, в то время не было алгебры, греки не знали десятичных дробей, не оперировали понятием ноля, иррациональных чисел и многими другими привычными нам элементами математики. Так что решение этой задачи вылилось в целый трактат «О шаре и цилиндре», который содержал еще кучу важной геометрической информации, полученной Архимедом в качестве промежуточных результатов.

Архимед настолько гордился этой работой, что просил выбить на своей могиле изображение цилиндра с вписанным в него шаром с отношением их объемов. Много лет спустя, посетив Сиракузы, Цицерон утверждал, что нашел это надгробие с выбитым кубом, в который были вписаны цилиндр и шар. И не просто нашел, а распорядился привести заросшую могилу в порядок и ухаживать за ней. Увы, затем все вновь пришло в запустение, и могила была повторно утеряна, теперь уже навсегда.

Сегодня память об Архимеде живет в виде множества картин, почтовых марок и проч. А еще профиль Архимеда и его слова «Превзойти свою человеческую ограниченность и покорить Вселенную» выбиты на медали лауреата премии Филдса – аналога Нобелевской премии для математиков.

Источник