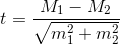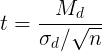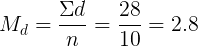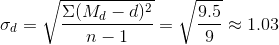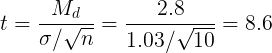Критерий стьюдента равен 0 что это значит
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
t-КРИТЕРИЙ СТЬЮДЕНТА ДЛЯ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ
– общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

1. История разработки t-критерия
Данный критерий был разработан Уильямом Сили Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
3. В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
4. Как рассчитать t-критерий Стьюдента?
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
5. Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
6. Пример расчета t-критерия Стьюдента
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА
– одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.

1. История разработки t-критерия
t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется парный t-критерий Стьюдента?
3. В каких случаях можно использовать парный t-критерий Стьюдента?
Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.
Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.
Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.
4. Как рассчитать парный t-критерий Стьюдента?
Парный t-критерий Стьюдента рассчитывается по следующей формуле:
5. Как интерпретировать значение t-критерия Стьюдента?
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p
3. Найдем среднее квадратическое отклонение разностей от средней по формуле:
4. Рассчитаем парный t-критерий Стьюдента:
Таблица критических значений t-критерия Стьюдента
В таблице критических значений t-критерия Стьюдента находятся теоретические значения критерия.
| df | p=0,05 | p=0,01 | p=0,001 |
| 1 | 12,70 | 63,65 | 636,61 |
| 2 | 4,303 | 9,925 | 31,602 |
| 3 | 3,182 | 5,841 | 12,923 |
| 4 | 2,776 | 4,604 | 8,610 |
| 5 | 2,571 | 4,032 | 6,869 |
| 6 | 2,447 | 3,707 | 5,959 |
| 7 | 2,365 | 3,499 | 5,408 |
| 8 | 2,306 | 3,355 | 5,041 |
| 9 | 2,262 | 3,250 | 4,781 |
| 10 | 2,228 | 3,169 | 4,587 |
| 11 | 2,201 | 3,106 | 4,437 |
| 12 | 2,179 | 3,055 | 4,318 |
| 13 | 2,160 | 3,012 | 4,221 |
| 14 | 2,145 | 2,977 | 4,140 |
| 15 | 2,131 | 2,947 | 4,073 |
| 16 | 2,120 | 2,921 | 4,015 |
| 17 | 2,110 | 2,898 | 3,965 |
| 18 | 2,101 | 2,878 | 3,922 |
| 19 | 2,093 | 2,861 | 3,883 |
| 20 | 2,086 | 2,845 | 3,850 |
| 21 | 2,080 | 2,831 | 3,819 |
| 22 | 2,074 | 2,819 | 3,792 |
| 23 | 2,069 | 2,807 | 3,768 |
| 24 | 2,064 | 2,797 | 3,745 |
| 25 | 2,060 | 2,787 | 3,725 |
| 26 | 2,056 | 2,779 | 3,707 |
| 27 | 2,052 | 2,771 | 3,690 |
| 28 | 2,049 | 2,763 | 3,674 |
| 29 | 2,045 | 2,756 | 3,659 |
| 30 | 2,042 | 2,750 | 3,646 |
| 31 | 2,040 | 2,744 | 3,633 |
| 32 | 2,037 | 2,738 | 3,622 |
| 33 | 2,035 | 2,733 | 3,611 |
| 34 | 2,032 | 2,728 | 3,601 |
| 35 | 2,030 | 2,724 | 3,591 |
| 36 | 2,028 | 2,719 | 3,582 |
| 37 | 2,026 | 2,715 | 3,574 |
| 38 | 2,024 | 2,712 | 3,566 |
| 39 | 2,023 | 2,708 | 3,558 |
| 40 | 2,021 | 2,704 | 3,551 |
| 41 | 2,020 | 2,701 | 3,544 |
| 42 | 2,018 | 2,698 | 3,538 |
| 43 | 2,017 | 2,695 | 3,532 |
| 44 | 2,015 | 2,692 | 3,526 |
| 45 | 2,014 | 2,690 | 3,520 |
| 46 | 2,013 | 2,687 | 3,515 |
| 47 | 2,012 | 2,685 | 3,510 |
| 48 | 2,011 | 2,682 | 3,505 |
| 49 | 2,010 | 2,680 | 3,500 |
| 50 | 2,009 | 2,678 | 3,496 |
| 51 | 2,008 | 2,676 | 3,492 |
| 52 | 2,007 | 2,674 | 3,488 |
| 53 | 2,006 | 2,672 | 3,484 |
| 54 | 2,005 | 2,670 | 3,480 |
| 55 | 2,004 | 2,688 | 3,476 |
| 56 | 2,003 | 2,667 | 3,473 |
| 57 | 2,002 | 2,665 | 3,470 |
| 58 | 2,002 | 2,663 | 3,466 |
| 59 | 2,001 | 2,662 | 3,463 |
| 60 | 2,000 | 2,660 | 3,460 |
| 61 | 2,000 | 2,659 | 3,457 |
| 62 | 1,999 | 2,657 | 3,454 |
| 63 | 1,998 | 2,656 | 3,452 |
| 64 | 1,998 | 2,655 | 3,449 |
| 65 | 1,997 | 2,654 | 3,447 |
| 66 | 1,997 | 2,652 | 3,444 |
| 67 | 1,996 | 2,651 | 3,442 |
| 68 | 1,995 | 2,650 | 3,439 |
| 69 | 1,995 | 2,649 | 3,437 |
| 70 | 1,994 | 2,648 | 3,435 |
| 71 | 1,994 | 2,647 | 3,433 |
| 72 | 1,993 | 2,646 | 3,431 |
| 73 | 1,993 | 2,645 | 3,429 |
| 74 | 1,993 | 2,644 | 3,427 |
| 75 | 1,992 | 2,643 | 3,425 |
| 76 | 1,992 | 2,642 | 3,423 |
| 77 | 1,991 | 2,641 | 3,422 |
| 78 | 1,991 | 2,640 | 3,420 |
| 79 | 1,990 | 2,639 | 3,418 |
| 80 | 1,990 | 2,639 | 3,416 |
| 90 | 1,987 | 2,632 | 3,402 |
| 100 | 1,984 | 2,626 | 3,390 |
| 110 | 1,982 | 2,621 | 3,381 |
| 120 | 1,980 | 2,617 | 3,373 |
| 130 | 1,978 | 2,614 | 3,367 |
| 140 | 1,977 | 2,611 | 3,361 |
| 150 | 1,976 | 2,609 | 3,357 |
| 200 | 1,972 | 2,601 | 3,340 |
| 250 | 1,969 | 2,596 | 3,330 |
| 300 | 1,968 | 2,592 | 3,323 |
| 350 | 1,967 | 2,590 | 3,319 |
Вы просмотрели статью критерий стьюдента таблица.
Что значит, когда t-критерий Стьюдента получается меньше 0?
Для связанных выборок:
На одной выборке проводили формирующий эксперимент. Например, стимулировали разными методами рост художественно-эстетической ориентации личности. Оценили тестом эту ориентацию у группы до эксперимента и после.
Подсчитав критерий Стьюдента, оказалось, что различия статистически значимые tэмп>tкрит. Другими словами, стимулирование способствовало изменению уровня художественно-эстетической ориентации испытуемых, и это изменение статистически значимо. Точнее среднее значение этого уровня в группе испытуемых.
Если за первую выборку (X) мы примем результаты оценивающего теста до эксперимента, а за вторую выборку (Y) результаты теста после эксперимента. (И рост баллов, которые получают испытуемые за оценивающий тест, отражают рост художественно-эстетической ориентации личности. То есть тест оценивает, чем больше баллов, тем сильнее ориентация).
То тогда, знак (+) покажет, что формирующий эксперимент был неудачным, а поскольку t-Стьюдента значимое, даже разрушительным. Изменения произошли в обратную сторону: испытуемые, в среднем больше склонялись к художественно-эстетической ориентации до эксперимента, чем после его завершения.
А вот если tэмп имеет знак (-), значит средние полученные баллы по тесту в выборке Y (после эксперимента) больше средних баллов в выборке X (до эксперимента). Поэтому формирующий эксперимент признан удачным, после стимулирования среднее значение художественно-эстетической ориентации у испытуемых увеличилось, и это увеличение статистически значимое.
6.1 Параметрические критерии
В группу параметрических критериев методов математической статистики входят методы для вычисления описательных статистик, построения графиков на нормальность распределения, проверка гипотез о принадлежности двух выборок одной совокупности. Эти методы основываются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения. Среди параметрических критериев статистики нами будут рассмотрены критерий Стьюдента и Фишера.
6.1.1 Методы проверки выборки на нормальность
Чтобы определить, имеем ли мы дело с нормальным распределением, можно применять следующие методы:
1) в пределах осей можно нарисовать полигон частоты (эмпирическую функцию распределения) и кривую нормального распределения на основе данных исследования. Исследуя формы кривой нормального распределения и графика эмпирической функции распределения, можно выяснить те параметры, которыми последняя кривая отличается от первой;
2) вычисляется среднее, медиана и мода и на основе этого определяется отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.
3) эксцесс кривой распределения должен быть равен 0. Кривые с положительным эксцессом значительно вертикальнее кривой нормального распределения. Кривые с отрицательным эксцессом являются более покатистыми по сравнению с кривой нормального распределения;
4) после определения среднего значения распределения частоты и стандартного oтклонения находят следующие четыре интервала распределения сравнивают их с действительными данными ряда:
а) 
б) 
в) 
г) 
6.1.2 Критерий Стьюдента ( t-критерий)
Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».
При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.
Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.
Статистика критерия для случая несвязанных, независимых выборок равна:

где 



где n 1 и n 2 соответственно величины первой и второй выборки.
Если n 1= n 2, то стандартная ошибка разности средних арифметических будет считаться по формуле:

где n величина выборки.
Подсчет числа степеней свободы осуществляется по формуле:
Далее необходимо сравнить полученное значение t эмп с теоретическим значением t—распределения Стьюдента (см. приложение к учебникам статистики). Если t эмп t крит, то гипотеза H 0 принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.
Таблица 1. Результаты эксперимента
Первая группа (экспериментальная) N 1=11 человек
Вторая группа (контрольная)
12 14 13 16 11 9 13 15 15 18 14
13 9 11 10 7 6 8 10 11
Общее количество членов выборки: n 1=11, n 2=9.
Расчет средних арифметических: Хср=13,636; Y ср=9,444
Стандартное отклонение: s x=2,460; s y =2,186
По формуле (2) рассчитываем стандартную ошибку разности арифметических средних:
Считаем статистику критерия:
Сравниваем полученное в эксперименте значение t с табличным значением с учетом степеней свободы, равных по формуле (4) числу испытуемых минус два (18).
Табличное значение tкрит равняется 2,1 при допущении возможности риска сделать ошибочное суждение в пяти случаях из ста (уровень значимости=5 % или 0,05).
Если полученное в эксперименте эмпирическое значение t превышает табличное, то есть основания принять альтернативную гипотезу (H1) о том, что учащиеся экспериментальной группы показывают в среднем более высокий уровень знаний. В эксперименте t=3,981, табличное t=2,10, 3,981>2,10, откуда следует вывод о преимуществе экспериментального обучения.
Здесь могут возникнуть такие вопросы:
1. Что если полученное в опыте значение t окажется меньше табличного? Тогда надо принять нулевую гипотезу.
2. Доказано ли преимущество экспериментального метода? Не столько доказано, сколько показано, потому что с самого начала допускается риск ошибиться в пяти случаях из ста (р=0,05). Наш эксперимент мог быть одним из этих пяти случаев. Но 95% возможных случаев говорит в пользу альтернативной гипотезы, а это достаточно убедительный аргумент в статистическом доказательстве.
3. Что если в контрольной группе результаты окажутся выше, чем в экспериментальной? Поменяем, например, местами, сделав 

Отсюда следует вывод, что новый метод пока не проявил себя с хорошей стороны по разным, возможно, причинам. Поскольку абсолютное значение 3,9811>2,1, принимается вторая альтернативная гипотеза (Н2) о преимуществе традиционного метода.
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.
Вычисление значения t осуществляется по формуле:

Sd вычисляется по следующей формуле:

Если t эмп t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 2. Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест. Из методических соображений в таблице 2 приводятся результаты небольшого числа испытуемых. [2]
Таблица 2. Результаты эксперимента
до начала эксперимента (Х)
Вначале произведем расчет по формуле:
Затем применим формулу (6), получим:
И, наконец, следует применить формулу (5). Получим:
Число степеней свободы: k =10-1=9 и по таблице Приложения 1 находим tкрит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтернативной гипотезы (H1) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.
6.1.3 F — критерий Фишера
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:

где 
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице.
Число степеней свободы определяется также просто:
В Приложении 1 критические значения критерия Фишера находятся по величинам k 1 (верхняя строчка таблицы) и k 2 (левый столбец таблицы).
Если t эмп> t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. [3] Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
Рассчитав дисперсии для переменных X и Y, получаем:
Тогда по формуле (8) для расчета по F критерию Фишера находим:
6.2 Непараметрические критерии
Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.
6.2.1 Критерий знаков ( G-критерий)
Критерий предназначен для сравнения состояния некоторого свойства у членов двух зависимых выборок на основе измерений, сделанных по шкале не ниже ранговой.
Нулевая гипотеза формулируются следующим образом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно различны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.
Статистика критерия (Т) определяется следующим образом:
Пример 4. Учащиеся выполняли контрольную работу, направленную на проверку усвоения некоторого понятия. Пятнадцати учащимся затем предложили электронное пособие, составленное с целью формирования данного понятия у учащихся с низким уровнем обучаемости. После изучения пособия учащиеся снова выполняли ту же контрольного работу, которая оценивалась по пятибалльной системе.
Результаты двукратного выполнения работы представляют измерения по шкале порядка (пятибалльная шкала). В этих условиях возможно применение знакового критерия для выявления тенденции изменения состояния знаний учащихся после изучения пособия, так как выполняются все допущения этого критерия.
Результаты двукратного выполнения работы (в баллах) 15 учащимися запишем в форме таблицы (см. табл. 1). [4]