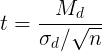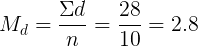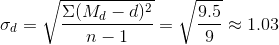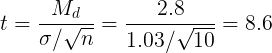Критерий стьюдента что показывает
Критерий стьюдента что показывает
Критерий t Стьюдента направлен на оценку различий величин средних и двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.
Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда выражение (9.2) будет вычисляться следующим образом:
В обоих случаях подсчет числа степеней свободы осуществляется по формуле:
где n1 и n2 соответственно величины первой и второй выборки.
Пример : Психолог измерял время сложной сенсомоторной реакции выбора
(в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающихся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.
Результаты эксперимента представим в виде табл. 9, в которой произведем ряд необходимых расчетов:
| № | Группы | Отклонение от среднего | Квадраты отклонения | |||
| X | Y | |||||
| 1 | 504 | 580 | — 22 | — 58 | 484 | 3368 |
| 2 | 560 | 692 | 34 | 54 | 1156 | 2916 |
| 3 | 420 | 700 | — 106 | 62 | 11236 | 3844 |
| 4 | 600 | 621 | 74 | — 17 | 5476 | 289 |
| 5 | 580 | 640 | 54 | — 2 | 2916 | 4 |
| 6 | 530 | 561 | 4 | — 77 | 16 | 5929 |
| 7 | 490 | 680 | — 36 | 42 | 1296 | 1764 |
| 8 | 580 | 630 | 54 | — 8 | 2916 | 64 |
| 9 | 470 | — | — 56 | — | 3136 | — |
| Сумма | 4734 | 5104 | 0 | 0 | 28632 | 18174 |
| Среднее | 526 | 638 | ||||
Разница по абсолютной величине между средними
Подсчет выражения дает:
Число степеней свободы = 9 + 8-2= 15. По табл. 17 приложения 6 для данного числа степеней свободы находим :
Строим «ось значимости»:
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,]% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом.
Вычисления значений осуществляется по формуле:
В свою очередь вычисляется по следующей формуле:
Пример: Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач. Решение задачи представим в виде табл. 10.
| № испытуемых | 1 задача | 2 задача | ||
| 1 | 4,0 | 3,0 | 1,0 | 1,0 |
| 2 | 3,5 | 3,0 | 0,5 | 0,25 |
| 3 | 4,1 | 3,8 | 0,3 | 0,09 |
| 4 | 5,5 | 2,1 | 3,4 | 11,56 |
| 5 | 4,6 | 4,9 | -0,3 | 0,09 |
| 6 | 6,0 | 5,3 | 0,7 | 0,49 |
| 7 | 5,1 | 3,1 | 2,0 | 4,00 |
| 8 | 4,3 | 2,7 | 1,6 | 2,56 |
| Суммы | 37,1 | 27,9 | 9,2 | 20,04 |
Вначале произведем расчет по формуле:
Затем применим формулу:
И, наконец, следует применить формулу. Получим:
Строим «ось значимости»:
Измерение может быть проведено в шкале интервалов и отношений.
Сравниваемые выборки должны быть распределены по нормальному закону.
Критерий Стьюдента
Материал из MachineLearning.
Содержание
t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называют гипотезой сдвига).
Все разновидности критерия Стьюдента являются параметрическими и основаны на дополнительном предположении о нормальности выборки данных. Поэтому перед применением критерия Стьюдента рекомендуется выполнить проверку нормальности. Если гипотеза нормальности отвергается, можно проверить другие распределения, если и они не подходят, то следует воспользоваться непараметрическими статистическими тестами.
Примеры задач
Чаще всего критерий Стьюдента применяется для проверки равенства средних значений в двух выборках.
Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.
Пример 2. Первая выборка — это значения некоторой характеристики состояния пациентов, записанные до лечения. Вторая выборка — это значения той же характеристики состояния тех же пациентов, записанные после лечения. Объёмы обеих выборок обязаны совпадать; более того, порядок элементов (в данном случае пациентов) в выборках также обязан совпадать. Такие выборки называются связными. Требуется выяснить, имеется ли значимое отличие в состоянии пациентов до и после лечения, или различия чисто случайны.
Пример 3. Первая выборка — это поля, обработанные агротехническим методом А. Вторая выборка — поля, обработанные агротехническим методом Б. Значения в выборках — это урожайность. Требуется выяснить, является ли один из методов эффективнее другого, или различия урожайности обусловлены случайными факторами.
Пример 4. Первая выборка — это дни, когда в супермаркете проходила промо-акция типа А (красные ценники со скидкой). Вторая выборка — дни промо-акции типа Б (каждая пятая пачка бесплатно). Значения в выборках — это показатель эффективности промо-акции (объём продаж, либо выручка в рублях). Требуется выяснить, какой из типов промо-акции более эффективен.
Варианты применения
Сравнение выборочного среднего с заданным значением
Дополнительное предположение: выборка простая и нормальная.
Нулевая гипотеза (выборочное среднее равно заданному числу ).
имеет распределение Стьюдента с степенями свободы, где
— выборочное среднее, — выборочная дисперсия.
Сравнение двух выборочных средних при известных дисперсиях
Нулевая гипотеза (средние в двух выборках равны).
Сравнение двух выборочных средних при неизвестных равных дисперсиях
Нулевая гипотеза (средние в двух выборках равны).
имеет распределение Стьюдента с степенями свободы, где
— выборочные дисперсии; — выборочные средние.
Сравнение двух выборочных средних при неизвестных неравных дисперсиях
Задача сравнения средних двух нормально распределённых выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. Точного решения этой задачи до настоящего времени нет. На практике используются различные приближения.
Дополнительное предположение: обе выборки простые и нормальные.
Нулевая гипотеза (средние в двух выборках равны).
— выборочные дисперсии; — выборочные средние.
где квантили определяются по-разному в различных приближениях:
Сравнение двух выборочных средних в связанных выборках
Нулевая гипотеза (средние в двух выборках равны).
Сравнение выборочных средних в связанных выборках ничем не отличается от сравнения среднего разности с нулём.
Сравнение разности средних с заданным значением
Нулевая гипотеза (средние в двух выборках отличаются на заданную величину).
Модифицированная первая выборка сравнивается с исходной второй выборкой с помощью одного из критериев, описанных выше.
История
Критерий был разработан Уильямом Госсеттом для оценки качества пива на пивоваренных заводах Гиннесса в Дублине (Ирландия). В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
ПАРНЫЙ t-КРИТЕРИЙ СТЬЮДЕНТА
– одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.

1. История разработки t-критерия
t-критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны, статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
2. Для чего используется парный t-критерий Стьюдента?
3. В каких случаях можно использовать парный t-критерий Стьюдента?
Основным условием является зависимость выборок, то есть сравниваемые значения должны быть получены при повторных измерениях одного параметра у одних и тех же пациентов.
Как и в случае сравнения независимых выборок, для применения парного t-критерия необходимо, чтобы исходные данные имели нормальное распределение. При несоблюдении этого условия для сравнения выборочных средних должны использоваться методы непараметрической статистики, такие как G-критерий знаков или Т-критерий Вилкоксона.
Парный t-критерий может использоваться только при сравнении двухвыборок. Если необходимо сравнить три и более повторных измерений, следует использовать однофакторный дисперсионный анализ (ANOVA) для повторных измерений.
4. Как рассчитать парный t-критерий Стьюдента?
Парный t-критерий Стьюдента рассчитывается по следующей формуле:
5. Как интерпретировать значение t-критерия Стьюдента?
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p
3. Найдем среднее квадратическое отклонение разностей от средней по формуле:
4. Рассчитаем парный t-критерий Стьюдента:
Основные статистические критерии. t-критерий Стьюдента
В целях проведения качественного исследования и получения достоверных результатов для дальнейшего анализа и принятия окончательного решения используют различные способы, методы и инструменты. Порой бывает неважно, в какой научной области или отрасли действует автор. Важно лишь грамотно подобрать и использовать необходимые критерии. Одними из таких универсальных параметров являются так называемые статистические критерии, среди которых особое внимание следует уделить t-критерию Стьюдента.
В целях проведения качественного исследования и получения достоверных результатов для дальнейшего анализа и принятия окончательного решения используют различные способы, методы и инструменты. Порой бывает неважно, в какой научной области или отрасли действует автор. Важно лишь грамотно подобрать и использовать необходимые критерии. Одними из таких универсальных параметров являются так называемые статистические критерии, среди которых особое внимание следует уделить t-критерию Стьюдента.
Что это такое?
t-критерий Стьюдента – это статистический метод исследования, позволяющий производить сравнение параметров из двух разных выборок, областей. По результатам такого анализа исследователь может делать вывод о сходстве или различии анализируемых объектов. Данный метод успешно используется как в повседневной жизни, так и в различных областях науки (психология, математика, экономика и пр.) и отраслях.
t-критерий Стьюдента чаще всего используется в целях установления взаимосвязи между элементами разных групп. Например, исследователь может анализировать поведение и состояние пациентов с хроническим заболеванием (например, сахарный диабет второго типа) и здоровых людей или имеющих сахарный диабет первого типа и пр.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Этапы применения t-критерия Стьюдента
При использовании t-критерия Стьюдента важно, чтобы объекты исследования или анализируемые выборки были распределены равномерно и имели хотя бы минимальное взаимодействие: относились к одной и той же среде, выполняли одно и то же задание и пр. Данное правило называется принципом нормального распределения, когда изучаемые явления/процессы:
t-критерий Стьюдента лучше всего использовать в случаях, когда известны средние значения выборки. Например, эксперт намерен проанализировать средний возраст жителей Сибири и средний возраст россиян по стране. При использовании указанной статистической методики он сможет проверить гипотезу: продолжительность жизни в Сибири дольше, чем в среднем по стране. Для этого достаточно сравнить средние показатели по указанному региону и России. Если отклонений в возрасте не будет, то гипотеза считается верной. Если же будет выявлено некое различие, то важно рассчитать это отклонение.
Схема применения t-критерия Стьюдента выглядит следующим образом:
Чаще всего сравнивают средние показатели конкретного явления, процесса и пр. Для расчета этого критерия можно воспользоваться следующей формулой:
Как используется t-критерий Стьюдента в разных областях науки?
t-критерий Стьюдента – универсальное средство для анализа ситуации, позволяющее установить наличие связей между разными группами элементов. В частности, он успешно применяется в психологии и медицине при проведении различных экспериментов и наблюдений. Исследователи могут сравнивать две группы людей с одним и тем же заболеванием на разных стадиях. Например, первая группа – лица с первичным инсультом, вторая группа – лица со вторичным (неоднократным) инсультом. Гипотеза может быть любой: продолжительность жизни и после первичного инсульта выше чем после вторичного или физическая активность лиц с первичным заболеванием лучше, чем со вторичным и пр.
Также t-критерий Стьюдента часто используется в экономике, когда требуется апробировать полученные исследователем результаты. Например, он может сравнивать показатели разных лет, выявлять их динамику и прогнозировать дальнейшее развитие событий (этих же показателей). Здесь автор эксперимента выдвигает гипотезу: анализируемые показатели увеличатся или наоборот уменьшатся.
Ярким примером применения t-критерия Стьюдента является следующая ситуация:

Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
Когда и как применять Критерий Стьюдента (t-test), проверка нормальности данных в среде R
Наступила осень, а значит, настало время для запуска нового тематического проекта «Статистический анализ с R». В нем мы рассмотрим статистические методы с точки зрения их применения на практике: узнаем какие методы существуют, в каких случаях и каким образом их проводить в среде R. На мой взгляд, Критерий Стьюдента или t-тест (от англ. t-test) идеально подходит в качестве введения в мир статистического анализа. Тест Стьюдента достаточно прост и показателен, а также требует минимум базовых знаний в статистике, с которыми читатель может ознакомиться в ходе прочтения этой статьи.
Примечание_1: здесь и в других статьях Вы не увидите формул и математических объяснений, т.к. информация рассчитана на студентов естественных и гуманитарных специальностей, которые делают лишь первые шаги в стат. анализе.
Примечание_2: перед прочтением, я рекомендую ознакомиться с этой статьей, чтобы вспомнить базовые понятия описательной статистики, такие как медиана, стандартное отклонение, квантили и прочее.
Что такое t-тест и в каких случаях его стоит применять
В начале следует сказать, что в статистике зачастую действует принцип бритвы Оккамы, который гласит, что нет смысла проводить сложный статистический анализ, если можно применить более простой (не стоит резать хлеб бензопилой, если есть нож). Именно поэтому, несмотря на свою простоту, t-тест является серьезным инструментом, если знать что он из себя представляет и в каких случаях его стоит применять.
Нормальное распределение данных и методы его оценки qqplot и shapiro.test
Нормальное распределение данных характерно для количественных данных, на распределение которых влияет множество факторов, либо оно случайно. Нормальное распределение характеризуется несколькими особенностями:
Давайте создадим случайную выборку с нормальным распределением на языке программирования R, где общее количество измерений = 100, среднее арифметическое = 5, а стандартное отклонение = 1. Затем отобразим его на графике в виде гистограммы:
Ваш график может слегка отличаться от моего, так как числа сгенерированы случайным образом. Как Вы видите, данные не идеально симметричны, но кажется сохраняют форму нормального распределения. Однако, мы воспользуемся более объективными методами определения нормальности данных.
Одним из наиболее простых тестов нормальности является график квантилей (qqplot). Суть теста проста: если данные имеют нормальное распределение, то они не должны сильно отклоняться от линии теоретических квантилей и выходить за пределы доверительных интервалов. Давайте проделаем этот тест в R.
Как видно из графика, наши данные не имеют серьезных отклонений от теоретического нормального распределения. Но порой при помощи qqplot невозможно дать однозначный ответ. В этом случае следует использовать тест Шапиро-Уилка, который основан на нулевой гипотезе, что наши данные распределены нормально. Если же P-значение менее 0.05 (p-value
Провести тест Шапиро-Уилка в R не составит труда. Для этого нужно всего лишь вызвать функцию shapiro.test, и в скобках вставить имя ваших данных. В нашем случае p-value должен быть значительно больше 0.05, что не позволяет отвергнуть нулевую гипотезу о том, что наши данные распределены нормально.
Запускаем t-тест Стьюдента в среде R
Итак, если данные из выборок имеют нормальное распределение, можно смело приступать к сравнению средних этих выборок. Существует три основных типа t-теста, которые применяются в различных ситуациях. Рассмотрим каждый из них с использованием наглядных примеров.
Одновыборочный критерий Стьюдента (one-sample t-test)
Одновыборочный t-тест следует выбирать, если Вы сравниваете выборку с общеизвестным средним. Например, отличается ли средний возраст жителей Северо-Кавказского Федерального округа от общего по России. Существует мнение, что климат Кавказа и культурные особенности населяющих его народов способствуют продлению жизни. Для того, чтобы проверить эту гипотезу, мы возьмем данные РосСтата (таблицы среднего ожидаемого продолжительности жизни по регионам России) и применим одновыборочный критерий Стьюдента. Так как критерий Стьюдента основан на проверке статистических гипотез, то за нулевую гипотезу будем принимать то, что различий между средним ожидаемым уровнем продолжительности по России и республикам Северного Кавказа нет. Если различия существуют, то для того, чтобы считать их статистически значимыми p-value должно быть менее 0.05 (логика та же, что и в вышеописанном тесте Шапиро-Уилка).
Загрузим данные в R. Для этого, создадим вектор со средними значениями по республикам Кавказа (включая Адыгею). Затем, запустим одновыборочный t-тест, указав в параметре mu среднее значение ожидаемого возраста жизни по России равное 70.93.
Несмотря на то, что у нас всего 7 точек в выборке, в целом они проходят тесты нормальности и мы можем на них полагаться, так как эти данные уже были усреднены по региону.
Загрузим данные в среду R. Кроме проверки нормальности данных, будет полезно построить «график с усами», на котором можно видеть медианы и разброс данных для обеих выборок.
Как видно из графика, медианы выборок не сильно отличаются друг от друга, однако разброс данных гораздо сильнее на севере. Проверим отличаются ли статистически средние значения при помощи функции t.test. Однако в этот раз на место параметра mu мы ставим имя второй выборки. Результаты теста, которые Вы видите на рисунке снизу, говорят о том, что средняя урожайность картофеля на севере статистически не отличается от урожайности на юге (p = 0.6339).
Двувыборочный для зависимых выборок ( dependent two-sample t-test )
Заключение
Статья получилась довольно длинной, зато теперь Вы знаете: что такое критерий Стьюдента и нормальное распределение; как при помощи функций qqplot и shapiro.test проверять нормальность данных в R; а также разобрали три типа t-тестов и провели их в среде R.
Сравнение двух средних в Excel — на http://arhiuch.ru/lab20.html
Здравствуйте! Благодарю за подробное пояснение по теме t-критерия. Пытаюсь провести сравнительный анализ в своей магистерской диссертации по двум независимым выборкам. Шкал у меня несколько. В результате анализа с помощью программы SPSS какие-то значения по критерию равенства дисперсий Ливиня оказались меньше 0,05. Насколько я понимаю, использование t-критерия в этом случае будет неправомерным. Что посоветуете в этом случае?
Здравствуйте! Спасибо за Ваш комментарий. К сожалению, ни с SPSS, ни с критерием Ливиня мне не доводилось работать, поэтому помочь не в силах.
Добрый день, извините, что не по теме. Пишу дипломную работу и мне нужно оценить 2 уравнения методом максимального правдоподобия в R. Нигде не могу найти про это в интернете.Вы не знаете как это можно сделать?
Здравствуйте, Ганс!
Да, профиль действительно не мой, поэтому вряд ли могу помочь. Однако, посмотрите вот эту статью про R пакет «systemfit»: https://cran.r-project.org/web/packages/systemfit/vignettes/systemfit.pdf
Здравствуйте, Айгуль!
Вот функция, которую Вы ищете: https://www.math.ucla.edu/
Здравствуйте! Подскажите какой (и как) построить график чтобы охарактеризовать характер отличий некоторых показателей в группе за полом? Результаты по критерию Т-Стьюдента. спасибо)
Здравствуйте, Богдана!
Надо построить так называемый «ящик с усами», по-английски — boxplot.
Для этого запустите команду boxplot внутри которой сравниваемые Вами колонки с данными:
boxplot(Column_1, Column_2)
В легенде также обычно указывают значение p-valueю
Если не сможете сами разобраться, кидайте на яндекс диск свой файл, я Вам покажу решение.
Здравствуйте, спасибо за статью. У меня есть некоторые вопросы по поводу проверки на нормальность. Можно ли принять нормальность данных на основе только графического анализа? У меня получилось так, что графически данные выглядят как нормальные (идеальная колоколообразная плотность и прямая квантилей), но формальные тесты показывают, что данные ненормальные (за исключением почему-то теста Пирсона).
https://yadi.sk/i/oS2f7XY8edU_Ng — вот данные, проверял первый столбик с объемом легких (LungCap). По логике вещей, они и должны быть нормальными, в основном физические хар-ки людей, такие как рост, вес и т.д. ведь распределены нормально.
Спасибо за интересный вопрос. Я с Вами абсолютно согласен: как мы и ожидаем в данном случае распределение Ваших данных близко к нормальному (что хорошо видно и на гистограмме, и на QQ plot). Игнорируйте Shapiro и спокойно используйте параметрические методы (например, t-test).
Shapiro test имеет ряд ограничений, одно из которых — его ненадежность при работе с относительно большими выборками. В этом случае малейшее отклонение от нормального распределения ведет к крайне малому значению p-value. По этой причине, рекомендуется прежде всего полагаться на QQ plot, подобнее об этом можете почитать здесь (там описан практически Ваш случай): https://stats.stackexchange.com/questions/284033/qq-plot-looks-normal-but-shapiro-wilk-test-says-otherwise/284035
«Результаты t-теста говорят о том, что средняя ожидаемая продолжительность жизни у жителей Северного Кавказа (74.6 лет) действительно выше, чем в среднем по России (70.93 лет), а результаты теста являются статистически значимыми (p ↓
Здравствуйте, Виталий!
Спасибо, что сообщили. Очепятка исправлена:-)
Добрый вечер! Как Вы доступно и легко объясняете!Спасибо!
Что Вы можете рассказать о тесте Колмогорова-Смирнова, тест пропорций и биноминальном тесте? в каких случаях их лучше использовать?
Вам спасибо, что читаете этот блог! Я думаю написать о некоторых из этих тестов в Августе-Сентябре этого года. Пока работаю над другими статьями (про R пакеты).