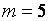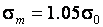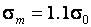Критерий сферичности бартлетта что показывает
10. Факторный анализ
Факторный анализ — представляет собой метод обобщения или сокращения большого количества переменных, объединение их в группы на основе характерных связей. В факторном анализе переменные не делятся на независимые и зависимые.
В практике маркетинговых исследований с факторный анализ применяется в следующих ситуациях
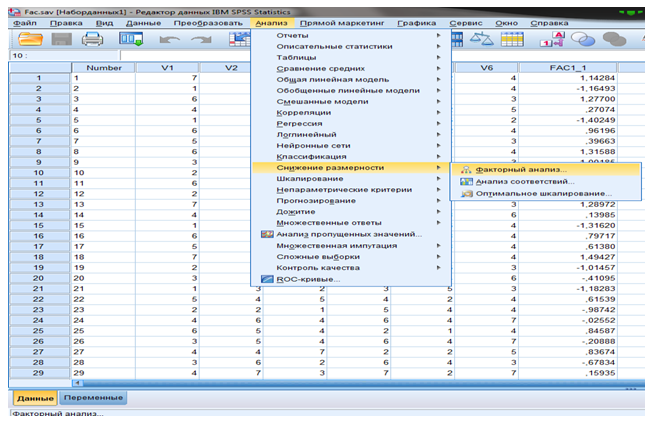
Факторный анализ применяется для выделения из большого массива данных малое число групп, состоящих из переменных, объединенных общими факторами (Рисунок 10.1).
Рисунок 10.1 –Диалоговое окно факторного анализа
В один фактор объединяются переменные, плотно коррелирующие между собой и слабо коррелирующие с переменными, которые объединяются на основе других факторов. Факторный анализ проводится с целью сокращения числа переменных и упрощение процедуры анализа существующей базы данных.
В процессе проведения факторного анализа рассчитываются и анализируются следующие показатели:
Графическое изображение критерия “каменистой осыпи” — график собственных значений факторов, расположенных в порядке убывания, используется для определения достаточного числа факторов.
Процедура факторного анализа включает следующие этапы:
Пример. Проведем факторный анализ с целью сокращения массива данных, содержащих информацию о мотивах туристов, при выборе места отдыха за городом. Оптимизируем структуру данных, сократив число переменных.
Мотивы туристов, при выборе места отдыха за городом:
Пошаговая инструкция
ШАГ 2. Из этого списка переменных выбрать необходимый массив, и перенести его в поле “Переменные”.
Если есть необходимость провести факторный анализ отдельно для двух переменных, например мужчин и женщин, то в поле “Переменная отбора наблюдений” вносится переменная “пол”. В данном случае нет необходимости проводить такое деление.
ШАГ 3. Диалоговое окно “Описательные статистики— выбрать “КМО и критерий сферичности Бартлетта” для проведения тестов “КМО” и “Бартлетт”, проверяющих пригодность данных для проведения факторного анализа.
ШАГ 4. Диалоговое окно “Описательные статистики— “Корреляционная матрица— “Коэффициенты— “Продолжить”.
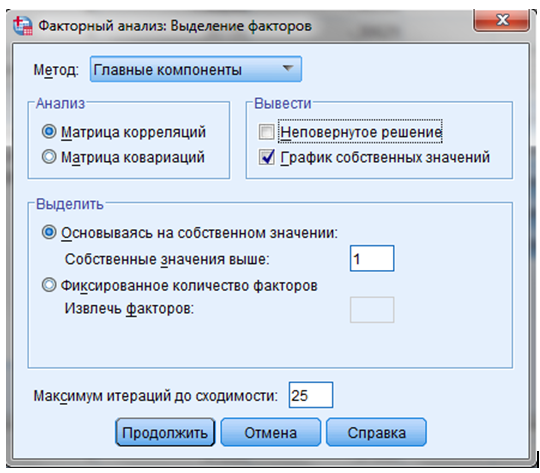
ШАГ 5. Диалоговое окно “Извлечение— задать условия определения количества факторов. В диалоговом окне “Извлечение— выбрать метод “Главные компоненты. — “Матрица корреляций” (Рисунок 10.2).
Рисунок 10.2 — Матрица корреляций
ШАГ 6. Задать условие: собственное значение больше “1”. При данном условии программа определит факторы в количестве больше 1.
ШАГ 7. Вывести график собственных значений — “График собственных значений— “Продолжить”.
ШАГ 8. Выбор ротации матрицы коэффициентов: в главном диалоговом окне “Факторный анализ— диалоговое окно “Вращение— метод ротации “Варимакс— “Продолжить”.
ШАГ 9. Создание новых переменных: в диалоговом окне “Факторный анализ— диалоговое окно “Значения факторов— отметить команду “Сохранить как переменные— метод расчета значений новых переменных “Регрессионная модель”. В итоге создаются новые переменные, которые можно будет использовать в дальнейшем анализе.
ШАГ 10. “ОК”.
Интерпретация результатов
Таблица 10.1 — Результаты теста КМО и Бартлетта
| близость к городу | приемлемые цены | близость водоема, леса | уровень комфорта | тишина, уединение | хорошее питание | наличие развлечений | комфорт отдыха с детьми | возможность лечения, ухода за здоровьем | организация детск. отдыха | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Корреляция | близость к городу | 1,000 | -,060 | ,009 | ,519 | -,172 | ,149 | ,322 | ,075 | -,166 | ,241 |
| приемлемые цены | -,060 | 1,000 | -,064 | -,341 | ,270 | -,247 | -,121 | ,232 | ,273 | -,407 | |
| близость водоема, леса | ,009 | -,064 | 1,000 | -,056 | ,017 | -,083 | ,107 | ,114 | ,027 | ,030 | |
| уровень комфорта | ,519 | -,341 | -,056 | 1,000 | -,113 | ,384 | ,070 | ,008 | -,125 | ,256 | |
| тишина, уединение | -,172 | ,270 | ,017 | -,113 | 1,000 | ,084 | -,167 | -,060 | ,989 | -,129 | |
| хорошее питани | ,149 | -,247 | -,083 | ,384 | ,084 | 1,000 | -,422 | ,191 | ,036 | ,237 | |
| наличие развлечений | ,322 | -,121 | ,107 | ,070 | -,167 | -,422 | 1,000 | -,045 | -,116 | ,248 | |
| комфорт отдыха с детьми | ,075 | ,232 | ,114 | ,008 | -,060 | ,191 | -,045 | 1,000 | -,053 | ,202 | |
| возможность лечения, ухода за здоровьем | -,166 | ,273 | ,027 | -,125 | ,989 | ,036 | -,116 | -,053 | 1,000 | -,106 | |
| организация детск. отдыха | ,241 | -,407 | ,030 | ,256 | -,129 | ,237 | ,248 | ,202 | -,106 | 1,000 |
Таблица 10.2 — Корреляционная матрица.
Коэффициенты корреляции характеризуют плотность связи между переменными исходного массива.
Метод выделения: Анализ главных компонент.
Начальные собственные значения должны быть больше 1.
Оптимальное число факторов — 5. Такая модель сохраняет 80,77% исходной информации, при этом число фактор сокращается в два раза.
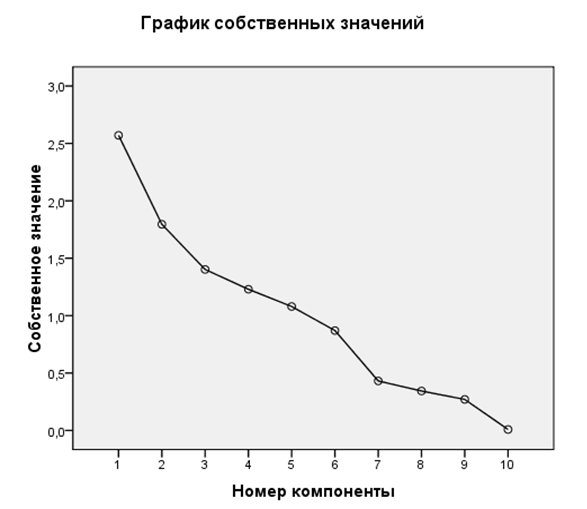
Рисунок 10.1 — График собственных значений
График показывает соответствующие собственные значения в системе координат: с 5 по 6 факторы происходит перелом графика. Это подтверждает, что оптимальное количество факторов 5.
Таблица 10.5 — Матрица повернутых компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.
| Компонента | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | -,69 | ,61 | ,023 | ,36 | -,12 |
| 2 | ,55 | ,48 | ,64 | ,19 | ,03 |
| 3 | ,45 | ,35 | ,75 | ,32 | ,002 |
| 4 | -,101 | -,008 | ,000 | ,14 | ,98 |
| ,51 | -,130 | -,83 | ,123 |
Таблица 10.6 — Матрица преобразования компонент
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.
Выделяем следующие факторы:
Фактор 1 — тишина и уединение, уход за здоровьем
Фактор 2 — близость к городу, уровень комфорта
Фактор 3 — хорошее питание, наличие развлечений
Фактор 4 — организация детского отдыха, близость водоем
Фактор 5 — комфорт отдыха с детьми, приемлемые цен
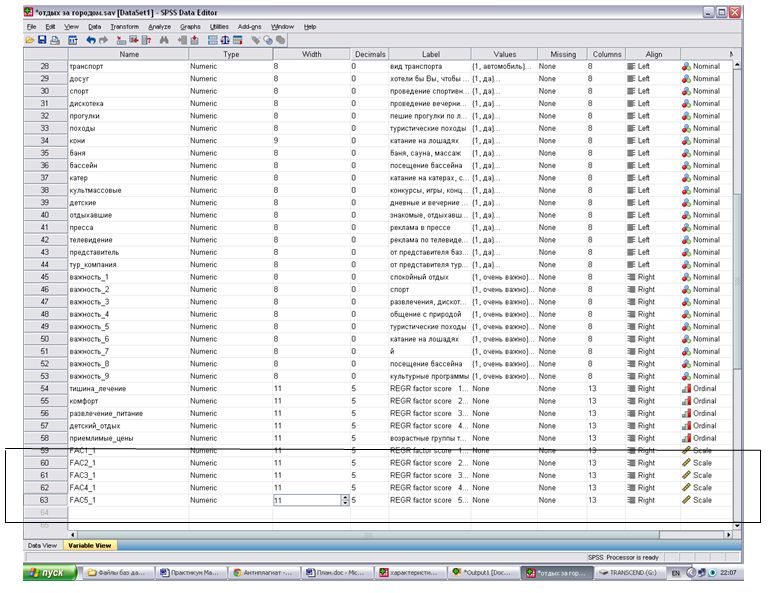
Рисунок 10.2 — Фрагмент вкладки “Переменные”
Названия новых компонент необходимо занести в исходную базу данных в столбец “Метка” таблицы “Переменные”, компьютер автоматически вычисляет значения новых переменных.
Суть новых переменных сводится к следующему: наибольшее отрицательное значение говорит о большей значимости переменной, и наоборот, наибольшее положительное значение говорит о наименьшей значимости переменной.
Созданные переменные в дальнейшем могут использоваться для анализа, например для проведения кластерного анализа.
Критерий Бартлетта
Материал из MachineLearning.
Критерий Бартлетта – статистический критерий, позволяющий проверять равенство дисперсий нескольких (двух и более) выборок. Нулевая гипотеза предполагает, что рассматриваемые выборки получены из генеральных совокупностей, обладающих одинаковыми дисперсиями.
Критерий Бартлетта является параметрическим и основан на дополнительном предположении о нормальности выборок данных. Поэтому перед применением критерия Бартлетта рекомендуется выполнить проверку нормальности. Критерий Бартлетта очень чувствителен к нарушению данного предположения.
Содержание
Примеры задач – применение критерия Бартлетта
Пример 1. Критерий Бартлетта может быть использован как вспомогательный – например, при проверке некоторого другого статистического теста, использующего равенство дисперсий. Приведем пример применения критерия Бартлетта в аналитической химии в качестве вспомогательного критерия. (См. Применение дисперсионного анализа в аналитической химии.) При проведении межлабораторных экспериментов возникает тип задач, когда один образец анализируется в нескольких лабораториях, а затем полученные результаты обрабатываются и обобщаются. Таким образом, есть выборок в общем случае различного размера. Необходимо сравнить средние значения полученных выборок. Для этого сперва нужно убедиться, что дисперсии однородны с помощью критерия Бартлетта. Если дисперсии неоднородны, то сравнение средних проводить нельзя.
Пример 2. (См. Портал Естественных Наук.) Измеряется размер некоторого изделия. Всего проводится серий экспериментов, состоящих из ( ) измерений. При этом серии измерений могут быть отнесены к разным экспериментаторам, могут применяться различные методики измерения. В условиях выполнения предположения о нормальности распределения необходимо сравнить выборки на однородность дисперсий.
Пример 3. (См. Обработка однотипных выборок экспериментальных данных.) По результатам наблюдения за пропускной способностью канала в различные дни испытаний сформированы упорядоченные выборки. При заданном уровне значимости необходимо проверить однородность выборок.
Описание критерия
Имеется выборок объемом ( ) каждая. Дисперсии выборок и выборочные оценки дисперсий обозначим через и соответственно.
Дополнительные предположения
Нулевая гипотеза
Критерий Бартлетта проверяет гипотезу о том, что дисперсии всех выборок одинаковы.
Альтернативная гипотеза : существует, по крайней мере, две выборки и ( ) с несовпадающими дисперсиями.
Статистика критерия Бартлетта
Статистика критерия Бартлетта вычисляется в соответствии с соотношением:
где и – суммарная оценка дисперсий.
При 3 (i=1. k) » alt= «n_i > 3 (i=1. k) » /> и справедливости нулевой гипотезы статистика критерия Бартлетта имеет распределение хи-квадрат с (k-1) степенями свободы.
Критерий (при уровне значимости )
Примечание
При отклонении от нормальности рекомендуется вместо статистики пользоваться ее модификацией:
Критерий сферичности бартлетта что показывает
Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального
Б.Ю. Лемешко, Е.П. Миркин
The classical statistic distributions building on samples series used in testing hypotheses on variances have been investigated by means of statistical modeling methods. The tables of percentage points of Bartlett’s and Cochran’s statistics, which can be used for correct testing hypotheses when observed laws are described with the exponential distribution family, have been obtained.
Key words : testing hypotheses, mathematical expectation, variance, percentage points, Bartlett’s test, Cochran’s test
Введение
При статистическом контроле качества для проверки наличия возмущения в ходе процесса, как правило, используется ряд статистических критериев, с помощью которых проверяются гипотезы о постоянстве дисперсий контролируемого показателя или о равенстве этого показателя номинальному значению. Аналогичные задачи проверки гипотез возникают в измерительных задачах. В литературных источниках [1, 2] и стандартах [3] в этих целях рассматривается применение критериев Бартлетта [4] и Кокрена [5]. Данные критерии применяются для проверки гипотез о равенстве дисперсий совокупности выборок. В [3] применение критерия Кокрена предусматривается для выделения выбросов при анализе физико-химических измерений.
Проверяемая гипотеза о постоянстве дисперсии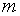 
выборок имеет вид:
а конкурирующая с ней гипотеза –
Например, в задаче контроля некоторого показателя гипотеза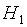 
может утверждать, что, по крайней мере, для двух моментов взятия выборок из общего числа моментов времени m ( m выборок, взятых в разные моменты времени) дисперсия имеет разные значения.
В качестве основного предположения при построении критериев Бартлетта и Кокрена и выводе предельных распределений статистик этих критериев выдвигалась принадлежность наблюдаемых случайных величин (погрешностей измерений) нормальному закону распределения.
Известно, что погрешности измерительных приборов далеко не всегда описываются нормальным законом распределения [6]. Очевидно и то, что в задачах контроля качества регистрируемые отклонения контролируемого показателя технологического процесса от номинального (заданного) значения при условии стационарности процесса не всегда подчиняются нормальному закону. При этом сам процесс может удовлетворять выдвигаемым требованиям, например, математическое ожидание – совпадать с номинальным значением показателя технологического процесса, а дисперсия – не превышать заданной величины.
Как поведут себя рассматриваемые критерии при нарушении предположений о нормальности погрешностей измерений? Возможно ли в изменившейся ситуации применение данных критериев в их классическом виде или такие действия приведут к некорректности результатов?
Цель данной работы состояла в исследовании распределений статистик вышеупомянутых критериев при различной степени отклонения распределения наблюдаемых случайных величин (погрешностей измерений) от нормального закона и в выработке рекомендаций по применению данных критериев в таких условиях. Представленные результаты дополняют исследования [7] о поведении статистик критериев, используемых для проверки гипотез о дисперсиях и математических ожиданиях. Как и в работе [7], в основе данных исследований лежала развиваемая методика статистического моделирования и компьютерного анализа, хорошо зарекомендовавшая себя при исследовании статистических закономерностей в [8, 9].
Критерий Бартлетта
Статистика критерия Бартлетта вычисляется в соответствии с соотношением [2]:
( 3)
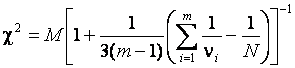
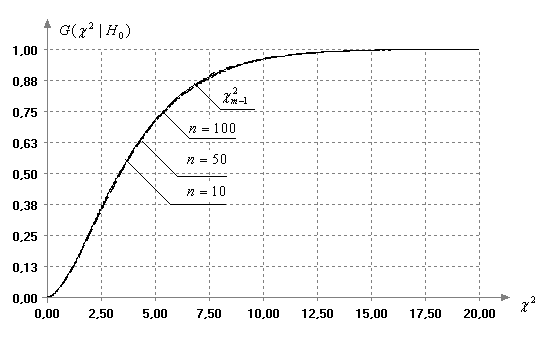
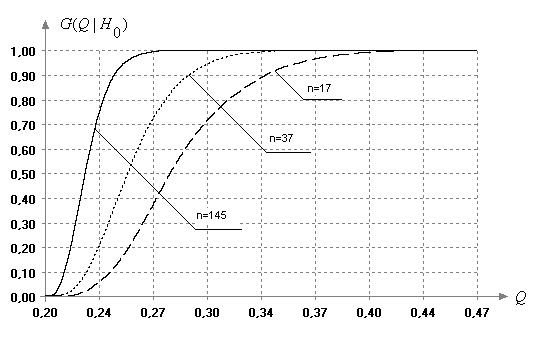
При нормально распределенных результатах измерений распределение статистики (3) практически не зависит от изменения объема выборки. Например, на рис. 1 приведены практически совпадающие функции распределения статистики критерия Бартлетта (3) при различных объемах выборок (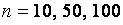 
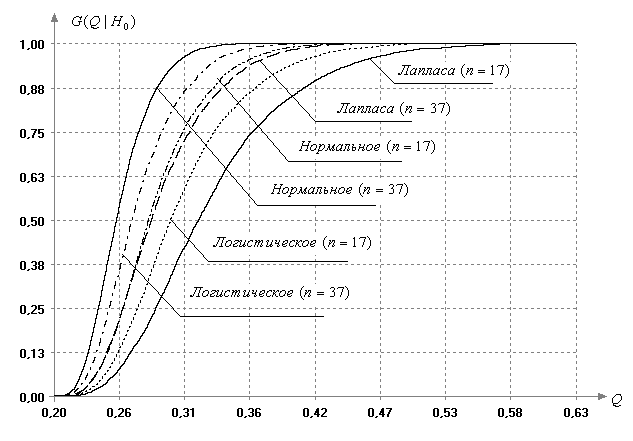
). Это означает, что в случае принадлежности результатов измерений нормальному закону выводы остаются корректными и при очень малых объемах анализируемых выборок.
В то же время, распределения статистики (3) очень чувствительны к отклонениям наблюдаемого закона от нормального. Вид распределения статистики (3) исследовался при различных наблюдаемых законах, в частности, в случае принадлежности моделируемых выборок законам логистическому с плотностью
Лапласа с плотностью
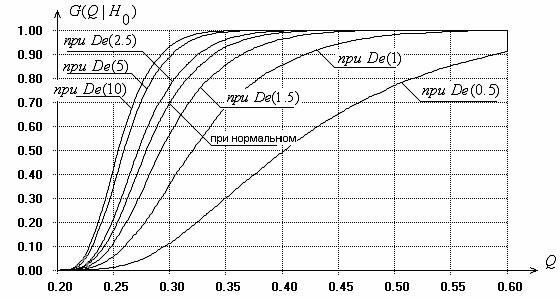
экспоненциальному семейству распределений с различными параметрами формы с плотностью
где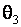 
– параметр формы. Законы нормальный и Лапласа являются частными случаями данного семейства распределений при значениях параметра формы 2 и 1 соответственно. Семейство (4) может быть хорошей моделью для законов распределения погрешностей различных измерительных систем.
Рис. 1. Функции распределения статистики классического критерия Бартлетта при различных объемах выборок при 
Рис. 2. Функции распределения статистики Бартлетта при отклонении закона распределения наблюдаемого показателя от нормального при различных объемах выборки и
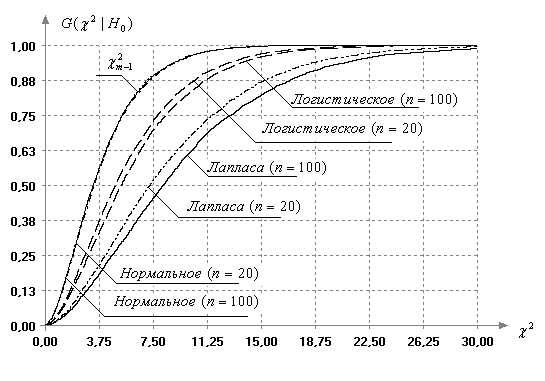
Рис. 3. Функции распределения статистики критерия Бартлетта в случае распределений экспоненциального семейства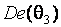 
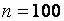
с различными значениями параметра формы при 
и
Критерий Кокрена
Распределения статистики Кокрена сильно зависят от объема наблюдаемых выборок. Поэтому в справочной литературе приводятся только таблицы процентных точек [2], которые и используются при проверке гипотез. На рис. 4 приведены полученные в результате компьютерного моделирования функции распределения статистики (5) при различных объемах выборок. В данном случае число оценок дисперсий m =5.
Рис. 4. Функции распределения статистики критерия Кокрена при различных объемах выборок при
Рис. 5. Функции распределения статистики критерия Кокрена при отклонении закона распределения наблюдаемого показателя от нормального при различных объемах выборки при
В [2] утверждается, что критерий Кокрена несколько уступает по мощности критерию Бартлетта. Распределения статистики Кокрена сильно зависят от объема выборок даже при нормальном законе и очень зависят от вида наблюдаемого закона. Казалось бы, что все это делает его мало привлекательным при произвольных наблюдаемых законах.
Рис. 6. Функции распределения статистики критерия Кокрена в случае распределений экспоненциального семейства с различными значениями параметра формы при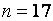 
и
Однако на самом деле, как показали наши исследования, в случае принадлежности наблюдений нормальному закону критерий Кокрена превосходит по мощности критерий Бартлетта.
: 
: 
: 
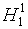
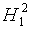
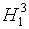
Критерий Бартлетта
Материал из MachineLearning.
Критерий Бартлетта – статистический критерий, позволяющий проверять равенство дисперсий нескольких (двух и более) выборок. Нулевая гипотеза предполагает, что рассматриваемые выборки получены из генеральных совокупностей, обладающих одинаковыми дисперсиями.
Критерий Бартлетта является параметрическим и основан на дополнительном предположении о нормальности выборок данных. Поэтому перед применением критерия Бартлетта рекомендуется выполнить проверку нормальности. Критерий Бартлетта очень чувствителен к нарушению данного предположения.
Содержание
Примеры задач – применение критерия Бартлетта
Пример 1. Критерий Бартлетта может быть использован как вспомогательный – например, при проверке некоторого другого статистического теста, использующего равенство дисперсий. Приведем пример применения критерия Бартлетта в аналитической химии в качестве вспомогательного критерия. (См. Применение дисперсионного анализа в аналитической химии.) При проведении межлабораторных экспериментов возникает тип задач, когда один образец анализируется в нескольких лабораториях, а затем полученные результаты обрабатываются и обобщаются. Таким образом, есть выборок в общем случае различного размера. Необходимо сравнить средние значения полученных выборок. Для этого сперва нужно убедиться, что дисперсии однородны с помощью критерия Бартлетта. Если дисперсии неоднородны, то сравнение средних проводить нельзя.
Пример 2. (См. Портал Естественных Наук.) Измеряется размер некоторого изделия. Всего проводится серий экспериментов, состоящих из ( ) измерений. При этом серии измерений могут быть отнесены к разным экспериментаторам, могут применяться различные методики измерения. В условиях выполнения предположения о нормальности распределения необходимо сравнить выборки на однородность дисперсий.
Пример 3. (См. Обработка однотипных выборок экспериментальных данных.) По результатам наблюдения за пропускной способностью канала в различные дни испытаний сформированы упорядоченные выборки. При заданном уровне значимости необходимо проверить однородность выборок.
Описание критерия
Имеется выборок объемом ( ) каждая. Дисперсии выборок и выборочные оценки дисперсий обозначим через и соответственно.
Дополнительные предположения
Нулевая гипотеза
Критерий Бартлетта проверяет гипотезу о том, что дисперсии всех выборок одинаковы.
Альтернативная гипотеза : существует, по крайней мере, две выборки и ( ) с несовпадающими дисперсиями.
Статистика критерия Бартлетта
Статистика критерия Бартлетта вычисляется в соответствии с соотношением:
где и – суммарная оценка дисперсий.
При 3 (i=1. k) » alt= «n_i > 3 (i=1. k) » /> и справедливости нулевой гипотезы статистика критерия Бартлетта имеет распределение хи-квадрат с (k-1) степенями свободы.
Критерий (при уровне значимости )
Примечание
При отклонении от нормальности рекомендуется вместо статистики пользоваться ее модификацией: