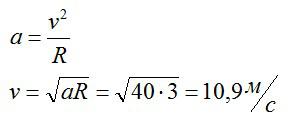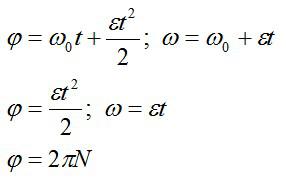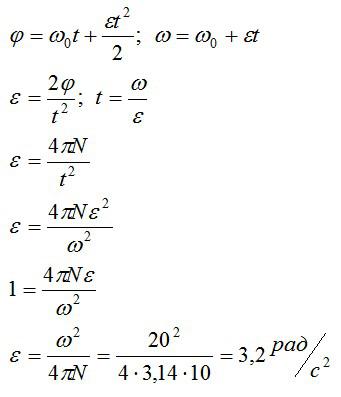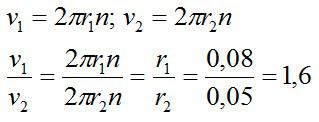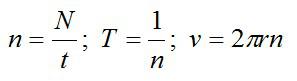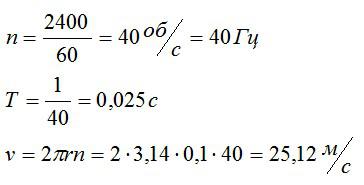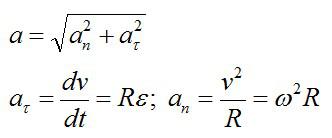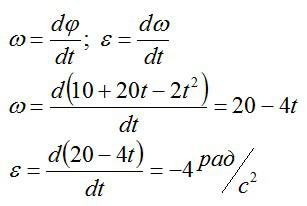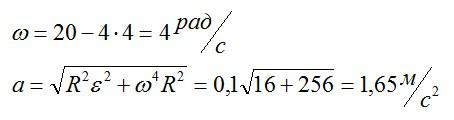Линейная скорость точки на ободе вращающегося диска в три раза больше чем
1.1 Элементы кинематики
UptoLike
Диск радиусом R = 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A + Bt3 (A = 2 рад; B = 4 рад/с3).
Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Bt2 (A = 0,3 м/с2; B = 0,1 м/с3). Определите угол α, который образует вектор полного ускорения a с радиусом колеса через 2 с от начала движения.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt2 (A = 0,1 рад/с2).
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt2 (A = 0,5 рад/с2).
Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением φ = A + Bt+ Сt2 + Dt3 (B = 1 рад/с, C = 1 рад/с2, D = 1 рад/с3).
Точка движется по окружности радиусом R = 15 см с постоянным тангенсальным ускорением aτ. К концу четвертого оборота после начала движения линейная скорость точки v1 = 15 см/с. Определить нормальное ускорение an2 точки через t2 = 16 c после начала движения.
Колесо автомобиля вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Якорь электродвигателя, имеющий частоту вращения n = 50 с-1, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря.
Колесо вращается с постоянным угловым ускорением ε = 3 рад/с. Определить радиус колеса, если через время t = 1 с после начала движения полное ускорение колеса равно а = 7,5 м/с2.
Линейная скорость v1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v2 точки, находящейся на 6 см ближе к его оси. Определите радиус диска.
Задачи на движение по окружности: примеры решения задач по кинематике
Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.
Движение по окружности: определение, примеры
Примеры движения по окружности:
Приведем ниже кинематические соотношения для поступательного и вращательного движений:
Вопросы на движение по окружности
Вопрос 1. Как направлено центростремительное ускорение?
Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.
Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?
Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.
Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?
Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.
Вопрос 4. Что такое линейная и угловая скорость?
Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?
Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.
Задачи на движение по окружности
Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение линейной скорости при движении по окружности
Условие
Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?
Решение
В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:
Ответ: 10,9 м/с.
Задача №2. Нахождение углового ускорения
Условие
Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение
Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:
Ответ: 3,2 радиан на секунду в квадрате.
Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.
Задача №3. Нахождение скорости движения по окружности
Условие
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Решение
Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:
Ответ: скорость точки на ободе больше в 1,6 раза.
Задача №4. Нахождение периода и частоты при движении по окружности
Условие
Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?
Решение
Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:
Ответ: 40 Гц; 0,025 с; 25,12 м/с.
Задача №5. Нахождение полного ускорения при движении по окружности
Условие
Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
Решение
Полное ускорение – векторная сумма нормального и тангенциального ускорений.
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:
Подставляем значение t из условия и вычисляем:
Ответ: 1,65 метра в секунду.
Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.
Задачи на движение по окружности: примеры решения задач по кинематике
Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.
Движение по окружности: определение, примеры
Примеры движения по окружности:
Приведем ниже кинематические соотношения для поступательного и вращательного движений:
Вопросы на движение по окружности
Вопрос 1. Как направлено центростремительное ускорение?
Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.
Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?
Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.
Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?
Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.
Вопрос 4. Что такое линейная и угловая скорость?
Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?
Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.
Задачи на движение по окружности
Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение линейной скорости при движении по окружности
Условие
Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?
Решение
В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:
Ответ: 10,9 м/с.
Задача №2. Нахождение углового ускорения
Условие
Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение
Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:
Ответ: 3,2 радиан на секунду в квадрате.
Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.
Задача №3. Нахождение скорости движения по окружности
Условие
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Решение
Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:
Ответ: скорость точки на ободе больше в 1,6 раза.
Задача №4. Нахождение периода и частоты при движении по окружности
Условие
Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?
Решение
Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:
Ответ: 40 Гц; 0,025 с; 25,12 м/с.
Задача №5. Нахождение полного ускорения при движении по окружности
Условие
Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
Решение
Полное ускорение – векторная сумма нормального и тангенциального ускорений.
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:
Подставляем значение t из условия и вычисляем:
Ответ: 1,65 метра в секунду.
Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.