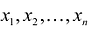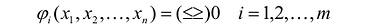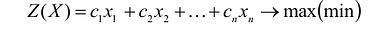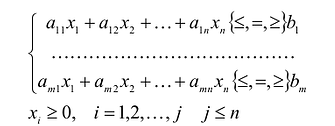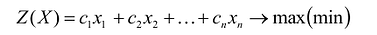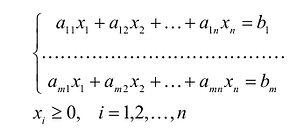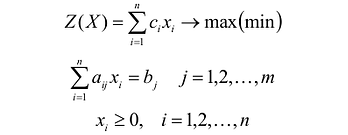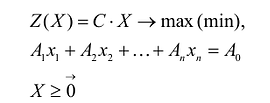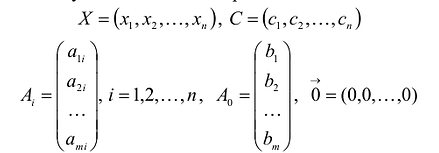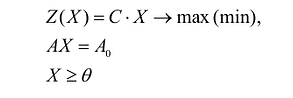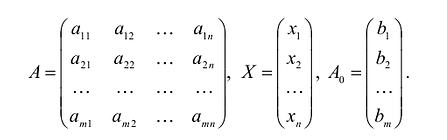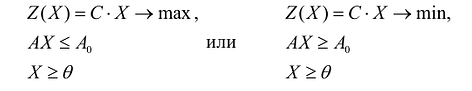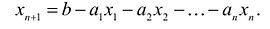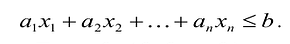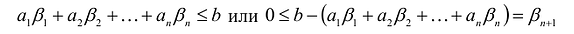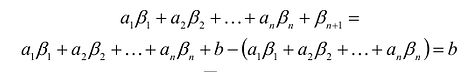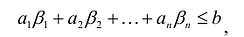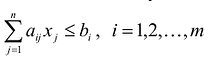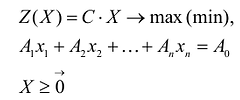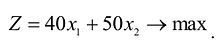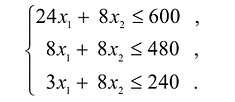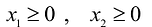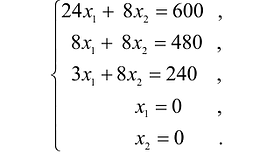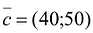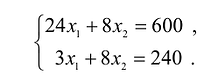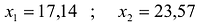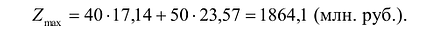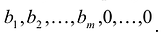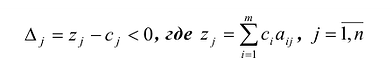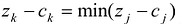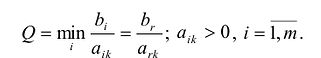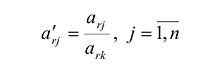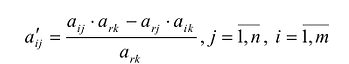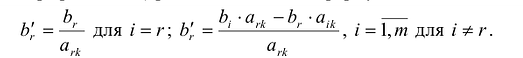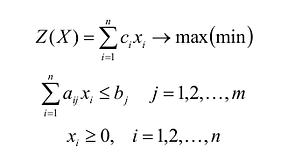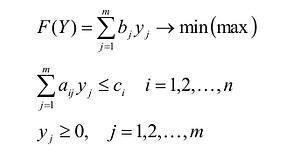Линейное программирование для чего нужно

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Источник

Table of Contents:

Компании должны максимально использовать то, что они имеют, когда дело доходит до ресурсов, таких как материалы, рабочая сила и деньги. Они также должны выбрать, как потратить свое время и усилия, чтобы максимизировать отдачу от своих инвестиций. Эти проблемы могут показаться простыми, но часто нужно учитывать множество переменных. Линейное программирование (ЛП) помогает предприятиям оптимизировать сложные операции, изображая различные решения в упрощенном виде. Как владелец бизнеса, важно, чтобы вы знали преимущества линейного программирования, а также его недостатки.

Линейное программирование в действии

Линейное программирование широко используется в науке управления и исследований, а также в бизнесе. Организации используют этот метод для оптимизации своих операций с целью снижения затрат и максимизации прибыли. Их конечной целью является достижение наилучшего возможного результата. Например, компания-производитель может использовать линейное программирование, чтобы определить способы минимизации производственных и складских расходов без ущерба для качества продукции.

Рассмотрим производителя велосипедов, который производит горные велосипеды и уличные велосипеды, каждый из которых приносит различный уровень прибыли. Производитель хотел бы знать, сколько велосипедов каждой категории производить, чтобы максимизировать прибыль, учитывая, что предприятие может продать всю свою продукцию.

Две разные команды производят горные велосипеды и уличные велосипеды вручную, каждая из которых имеет производственные ограничения с точки зрения количества велосипедов, которые она может производить в день. Велосипеды также должны пройти процесс машинной отделки, который имеет ограниченную производительность. Бизнес мог бы использовать метод линейного программирования для решения такого рода проблем.

Как и все остальное, этот метод не идеален. Перед его внедрением убедитесь, что вы хорошо понимаете преимущества и недостатки линейного программирования.

Ограничение: допущение о линейности

Подход линейного программирования основан на предположении, что мир линейен. В реальном мире это не всегда так. Существуют определенные способы смешивания входных данных, которые не допускаются подходом линейного программирования.

Например, производитель велосипедов может обнаружить, что, если он заказывает материалы для двух типов велосипедов у одного и того же поставщика, это может сократить расходы. Этот эффект не может быть включен в модель линейного программирования. Линейные модели также не учитывают определенные факторы, такие как повышение эффективности производства при повышении уровня производства.

Ограничение: дробные значения

Модель линейного программирования предполагает, что входы и выходы могут быть дробными. Это не всегда так в реальном мире. Например, если предприятие пытается выяснить, сколько человек должно быть в штате в часы наибольшей нагрузки, это не может быть долей.

Точно так же, если бизнес такси пытается решить, сколько автомобилей он должен купить, это тоже не может быть долей. Если хотя бы одна переменная должна быть в целочисленной форме, линейное программирование не подходит.

Преимущества линейного программирования

Несмотря на то, что линейное программирование имеет ряд недостатков, это универсальный метод, который можно использовать для представления ряда реальных ситуаций. Одним из основных преимуществ линейного программирования является то, что предприятия могут использовать эту технику для решения проблем, связанных с множеством переменных и ограничений. Использование компьютеров облегчило применение этой техники.

Этот метод может помочь предприятиям упростить свою деятельность, чтобы они могли выполнять больше задач за меньшее время и с меньшими затратами. Кроме того, это позволяет лучше принимать решения в широком диапазоне ситуаций. Например, компании могут использовать его для анализа финансовых или производственных проблем, определения решений и внесения корректировок на основе результатов.

Если вам известны преимущества и недостатки линейного программирования, вы узнаете, как лучше всего использовать этот метод для достижения желаемого результата. Рассмотрите его ограничения и решите, подходит ли он для вашей конкретной ситуации.

Фиксированный тариф Приоритетные почтовые ограничения на жидкости

Вы не можете отправлять наиболее опасные, легковоспламеняющиеся или взрывоопасные жидкости через USPS Priority Mail, а также существуют некоторые ограничения на скоропортящиеся жидкости.

Ограничения стратегий принятия решений в управлении

Бизнес использует модель линейного программирования

Источник

Зачем нужна математика бизнесмену? (Часть 6, последняя)

Отрывок из книги Ольги Соколовской “Он, она и математическая формула фирмы или Зачем математика бизнесмену?”

Часть 6

Историко-философское отступление

или Как применяют линейное программирование

В 1938 г. перед 25-летним профессором Ленинградского университета Л.В.Канторовичем была поставлена задача: как наилучшим образом распределить работу восьми станков фанерного треста при условии, что известна производительность каждого станка по каждому из пяти видов обрабатываемых материалов?

Ученый нашел метод решения этой задачи, который стал общим. Он получил название «Линейное программирование». В 1975 г. совместно с американским ученым Т. Купмансом Л.В. Канторович получил Нобелевскую премию за вклад в теорию оптимизации распределения ресурсов.

Методы линейного программирования применялись и одновременно развивались во время второй мировой войны для планирования военных операций. Еще до ее начала методы анализа военных систем на основе математического программирования стали использоваться военными специалистами в Великобритании, а затем и в других странах. В США и Канаде были созданы специальные подразделения, занимавшиеся анализом военных операций. В 1938 г. в США был введен термин «исследование операций» в качестве характеристики рода деятельности необычной исследовательской группы, выполнявшей работы по анализу военных систем, в частности решающих задачи оптимального использования радиолокационных установок в общей системе обороны страны. Этот анализ являлся основой для принятия командованием соответствующих решений.

Сегодня линейное и, шире, математическое программирование – один из основных методов принятия производственно-экономических решений. Существуют и другие методы: теория игр и статистических решений, метод Монте-Карло (статистических испытаний), теория массового обслуживания, сетевое планирование и др. Эти методы в совокупности объединяются названием «исследование операций».

В описании любой задачи исследования операций можно выделить достигаемые при решении задачи цели (сформулировать целевые функции, или оптимизируемые критерии), а также условия, ограничивающие возможные решения (условия – ограничения). Задачи исследования операций классифицируют по их теоретико-информационным свойствам. Если субъект в ходе принятия решения сохраняет свое информационное состояние (т.е. никакой информации не приобретает и не утрачивает), то принятие решения можно рассматривать как мгновенный акт. Соответствующие задачи называются статическими. Если же субъект в ходе принятия решения изменяет свое информационное состояние, получая или теряя информацию, то в такой динамической задаче обычно целесообразно принимать решение поэтапно (многошаговые решения). Значительная часть динамических задач исследования операций входит в динамическое программирование.

С конца 1940-х годов сфера приложения исследования операций стала охватывать разнообразные стороны человеческой деятельности – как чисто технические (особенно технологические), так и технико-экономические, а также управленческие различного уровня.

С 1950-х годов для исследования обоснования решений сложных проблем политического, социального, военного, экономического, научного и технического характера стала применяться совокупность методологических средств, получившая название системный анализ. Он приложим для решения таких задач, как распределение мощностей между различными видами изделий, определение потребности в новом оборудовании и в рабочей силе той или иной квалификации, прогнозирование спроса на различные виды продукции, а также развитие и техническое оснащение вооруженных сил, освоение космоса и т. д.

Системный анализ базируется на ряде прикладных математических дисциплин, в частности на исследовании операций. Когда в задаче системного анализа имеется одна четко выраженная цель, степень достижения которой можно оценить на основе одного критерия, как применяют линейное программирование.

Примерами задач, решаемых с помощью методов математического программирования, могут быть следующие:

Исследование операций во многих случаях остается единственным средством для принятия обоснованных решений. По словам профессора Е.С.Венцель исследование операций способно «дать плохой ответ на вопрос, на который нельзя ответить по-другому».

– Замечательно! Тогда я ставлю конкретный вопрос: если фирма выпускает, допустим, три вида продукции из двух видов сырья, как оптимально спланировать производство?

Вот теперь и попробуйте составить свой психологический портрет, который, надеюсь, поможет в Вашей профессиональной деятельности.

— Мне кажется, что наедине с собой, Вы, милый сударь, будете откровенней и сможете реальней оценить свои как положительные, так и отрицательные стороны Вашей натуры. «Умствуй и придет!» – повторял автор первого учебника по арифметике в Российской империи Л. Ф. Магницкий.

Мы устало замолчали. За окном поезда серело. Мы проговорили всю ночь. Вот показались пригородные дома, мы подъезжали к столице.

— Как долго Вы планируете быть в Киеве? – неожиданно спросил Александр Николаевич.

— Все зависит от того, как я управлюсь с делами. Надеюсь, не более 2-3 дней.

— Тогда я приглашаю Вас, дорогая учительница, сегодня на ужин.

— Не знаю, получится ли у меня…

Согласилась ли я? Ну, это совсем другая история, о которой, возможно, я расскажу в следующий раз…

Итак, уважаемый читатель сайта “Математический Тандем”, подведем итоги.

И в благодарность за то, что вы были на сайте и читали эту книгу,

дарю вам этот познавательный ролик.

Это запись передачи “Очевидное – невероятное”

с бессменным ведущим С. Капицей о том,

какое место занимает математематика в нашей жизни.

И не забудьте, пожалуйста поделиться с друзьями теми знаниями,

которые только что получили. Они Вам будут благодарны.

Об авторе

Мое педагогическое кредо: «Чтобы быть хорошим преподавателем, нужно любить то, что преподаешь, и любить тех, кому преподаешь.»

Источник

Содержание:

Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.

Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.

Построение математической модели экономической задачи включает следующие этапы:

Переменными задачи называются величины

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 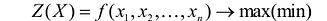и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:

Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:

Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (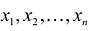). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любойX = (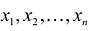). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

Используя знак суммирования эту задачу можно записать следующим образом:

Каноническая задача линейного программирования в векторной форме имеет вид:

В данном случае введены векторы:

Каноническая задача линейного программирования в матричной форме записи имеет вид:

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

прибавляется величина такая, что переводит неравенство в равенство , где:

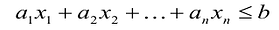
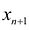
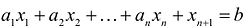
Неотрицательная переменная называется дополнительной переменной.

Основания для возможности такого преобразования дает следующая теорема.

Теорема. Каждому решению неравенства соответствует единственное решение уравнения: и неравенства и, наоборот, каждому решению уравнения: и неравенства соответствует единственное решение неравенства:

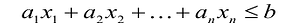
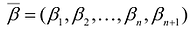
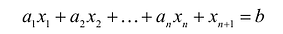
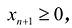
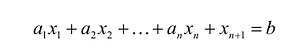
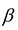
Доказательство. Пусть — решение неравенства. Тогда:

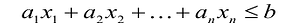
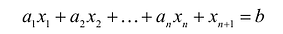
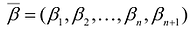
Если в уравнение вместо переменных подставить значения , получится:

Таким образом, решение удовлетворяет уравнению: и неравенству .

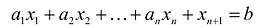
Доказана первая часть теоремы.

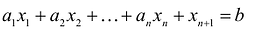
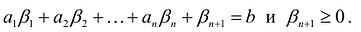
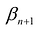
Пусть удовлетворяет уравнению и неравенству , т.е. . Отбрасывая в левой части равенства неотрицательную величину , получим:

т.е. удовлетворяет неравенству: что и требовалось доказать.

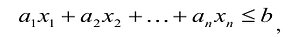
Если в левую часть неравенств системы ограничений вида

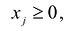
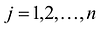
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Множества допустимых решений

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.

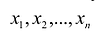
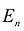
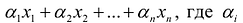
Выпуклой линейной комбинацией произвольных точек Евклидова пространства называется сумма — произвольные неотрицательные числа, сумма которых равна 1.

Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.

Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.

Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.

Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.

Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.

Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.

Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.

Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.

Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.

Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.

Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.

Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.

Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками

Каноническая задача линейного программирования в векторной форме имеет вид:

Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.

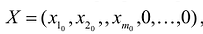
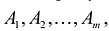
Опорным решением задачи линейного программирования называется такое допустимое решение , для которого векторы условий, соответствующие положительным координатам линейно независимы.

Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).

Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теорема. Любое опорное решение является угловой точкой области допустимых решений.

Теорема. Любая угловая точка области допустимых решений является опорным решением.

Пример:

Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.

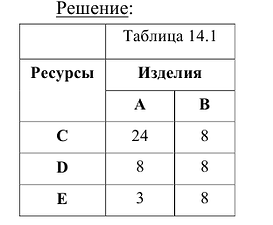
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1

Построим математическую модель задачи, для чего обозначим 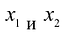— объемы производства изделий А и В соответственно.

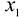
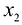
Тогда прибыль предприятия от реализации изделий А и изделий В составит:

Ограничения по ресурсам будут иметь вид:

Естественно, объемы производства должны быть неотрицательными

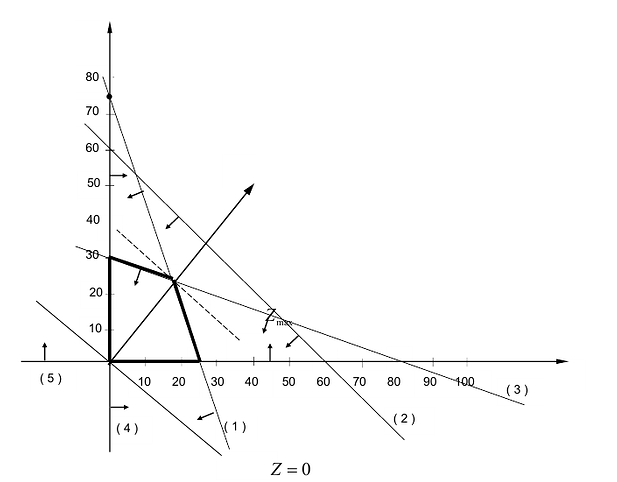
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:

Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

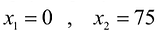
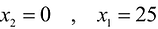
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: а при .

Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 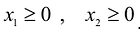, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.

Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции

имеет координаты

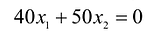
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.

Решив эту систему, получаем, что

Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:

Алгоритм решения задачи линейного программирования графическим методом таков:

В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

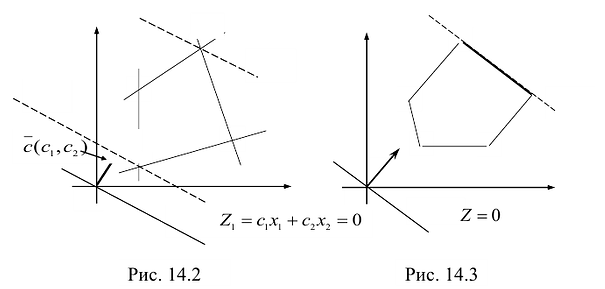
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.

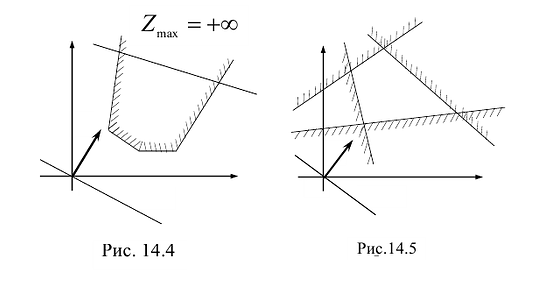
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.

Основные понятия симплексного метода решения задачи линейного программирования.

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.

Симплекс-метод основан на следующих свойствах задачи линейного программирования:

Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).

Симплекс-метод с естественным базисом

Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:

Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

Теорема 2. Если для всех векторов выполняется условие 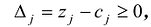то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 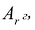, который дает минимальное положительное отношение:

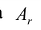
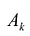
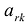
Строка называется направляющей, столбец и элемент — направляющими (последний называют также разрешающим элементом).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

а элементы любой другой i-й строки пересчитываются по формулам:

Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.

Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.

Симплексный метод с искусственным базисом (М-метод)

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Теория двойственности

Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.

Любую задачу линейного программирования можно записать в виде:

Первоначальная задача называется исходной или прямой.

Модель двойственной задачи имеет вид:

Переменные двойственной задачи 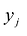называют объективно обусловленными оценками или двойственными оценками.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник