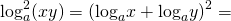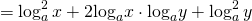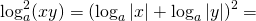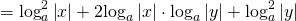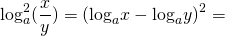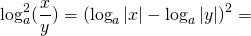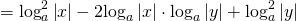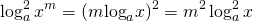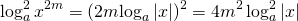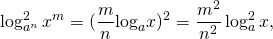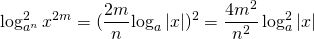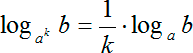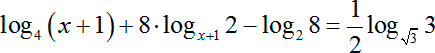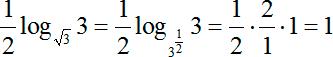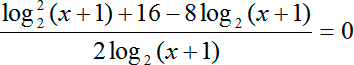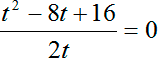Логарифм в квадрате что делать
Как возвести логарифм в квадрат
Как возвести логарифм в квадрат, когда под знаком логарифма стоит произведение или частное? Как упростить квадрат логарифма степени?
Как возвести в квадрат логарифм произведения.
Так как логарифм произведения равен сумме логарифмов, квадрат логарифма произведения равен квадрату суммы логарифмов множителей:
0,a \ne 1,x > 0,y > 0.\]» title=»Rendered by QuickLaTeX.com»/>
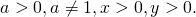
Если изменить условия:
0,a \ne 1,xy > o,\]» title=»Rendered by QuickLaTeX.com»/>
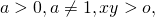
то каждый из множителей под знаком логарифма нужно брать по модулю:
Как возвести в квадрат логарифм частного.
Так как логарифм частного равен разности логарифмов, то квадрат логарифма частного равен квадрату разности логарифмов делимого и делителя:
0,a \ne 1,x > 0,y > 0.\]» title=»Rendered by QuickLaTeX.com»/>
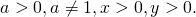
При изменении условий
0,a \ne 1,\frac
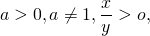
под знаком логарифма появляются модули:
Возведение в квадрат логарифма степени.
В логарифме степени показатель можно вынести за знак логарифма.
При возведении в квадрат логарифма степени показатель степени также следует возвести в квадрат:
0,a \ne 1,x > 0.\]» title=»Rendered by QuickLaTeX.com»/>
0,a \ne 1,x \ne 0,\]» title=»Rendered by QuickLaTeX.com»/>
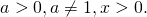
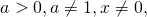
то при чётном показателе степени при вынесении показателя за знак логарифма под знаком логарифма появляется модуль:
Аналогично возводят в квадрат логарифм со степенью в основании:
0,a \ne 1,x > 0;\]» title=»Rendered by QuickLaTeX.com»/>
0,a \ne 1,x \ne 0.\]» title=»Rendered by QuickLaTeX.com»/>
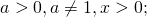
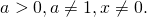
Основные свойства логарифмов
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.
Сложение и вычитание логарифмов
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!
Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Задача. Найдите значение выражения: log3 135 − log3 5.
Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.
Вынесение показателя степени из логарифма
Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Избавимся от степени в аргументе по первой формуле:
log7 49 6 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
[Подпись к рисунку]
[Подпись к рисунку]
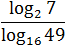
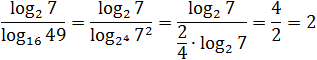
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.
Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
[Подпись к рисунку]
[Подпись к рисунку]
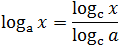
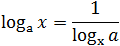
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Задача. Найдите значение выражения: log5 16 · log2 25.
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 2 4 = 4log5 2; log2 25 = log2 5 2 = 2log2 5;
А теперь «перевернем» второй логарифм:
[Подпись к рисунку]
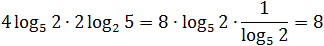
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Задача. Найдите значение выражения: log9 100 · lg 3.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
[Подпись к рисунку]
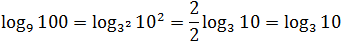
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
[Подпись к рисунку]
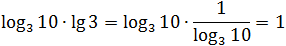
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.
Задача. Найдите значение выражения:
[Подпись к рисунку]
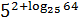
Заметим, что log25 64 = log5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
[Подпись к рисунку]
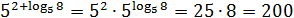
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂
Логарифмическая единица и логарифмический ноль
В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.
Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Уравнения, квадратные относительно логарифма, и прочие нестандартные приемы
На уравнениях такого вида многие ученики «зависают». При этом сами задачи отнюдь не являются сложными — достаточно просто выполнить грамотную замену переменной, для чего следует научиться выделять устойчивые выражения.
В дополнение к этому уроку вас ждет довольно объемная самостоятельная работа, состоящая из двух вариантов по 6 задач в каждом.
Метод группировки
Сегодня мы разберем два логарифмических уравнения, одно из которых не решается «напролом» и требует специальных преобразований, а второе. впрочем, не буду рассказывать все сразу. Смотрите видео, скачивайте самостоятельную работу — и учитесь решать сложные задачи.
Итак, группировка и вынесение общих множителей за скобку. Дополнительно я расскажу вам, какие подводные камни несет область определения логарифмов, и как небольшие замечания по области определений могут существенно менять как корни, так и все решение.
Начнем из группировки. Нам нужно решить следующее логарифмическое уравнение:
log2 x · log2 ( x − 3) + 1 = log2 ( x 2 − 3 x )
В первую очередь отметим, что x 2 − 3 x можно разложить на множители:
Затем вспоминаем замечательную формулу:
Сразу же небольшое замечание: данная формула прекрасно работает, когда а, f и g — обычные числа. Но когда вместо них стоят функции, данные выражения перестают быть равноправными. Представьте себе такую гипотетическую ситуацию:
f g fg будет положительным, следовательно, log a ( fg ) будет существовать, а вот log a f и log a g отдельно существовать не будут, и выполнить такое преобразование мы не сможем.
Игнорирование данного факта приведет к сужению области определения и, как следствие, к потере корней. Поэтому прежде чем выполнять такое преобразование, нужно обязательно заранее убедиться, что функции f и g положительные.
Следовательно, в функции log2 x ( x − 3) каждый множитель будет больше нуля. Поэтому можно смело раскладывать произведение на сумму:
log2 x log2 ( x − 3) + 1 − log2 x − log2 ( x − 3) = 0
На первый взгляд может показаться, что легче не стало. Напротив: количество слагаемых лишь увеличились! Чтобы понять, как действовать дальше, введем новые переменные:
А теперь сгруппируем третье слагаемое с первым:
( a · b − a ) + (1 − b ) = 0
a (1 · b − 1) + (1 − b ) = 0
Заметим, что и в первой, и во второй скобке стоит b − 1 (во втором случае придется вынести «минус» за скобку). Разложим нашу конструкцию на множители:
a (1 · b − 1) − ( b − 1) = 0
А теперь вспоминаем наше замечательно правило: произведение равно нулю, когда хотя бы один из множителей равен нулю:
Вспоминаем, что такое b и а. Получим два простейших логарифмических уравнения, в которых останется лишь избавиться от знаков logи приравнять аргументы:
Мы получили два корня, но это не решение исходного логарифмического уравнения, а лишь кандидаты в ответ. Теперь проверим область определения. Для первого аргумента:
Оба корня удовлетворяют первому требованию. Переходим ко второму аргументу:
А вот здесь уже x = 2 нас не удовлетворяет, зато x = 5 вполне нас устраивает. Следовательно, единственным ответом будет x = 5.
Переходим ко второму логарифмическому равнению. На первый взгляд, оно существенно проще. Однако в процессе его решения мы рассмотрим тонкие моменты, связанные с областью определения, незнание которых существенно усложняет жизнь начинающим ученикам.
log0,7 ( x 2 − 6 x + 2) = log0,7 (7 − 2 x )
Перед нами каноническая форма логарифмического уравнения. Ничего преобразовывать не нужно — даже основания одинаковые. Поэтому просто приравниваем аргументы:
x 2 − 6 x + 2 = 7 − 2 x
x 2 − 6 x + 2 − 7 + 2 x = 0
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
Но эти корни еще не являются окончательными ответами. Нужно найти область определения, поскольку в исходном уравнении присутствуют два логарифма, т.е. учет области определения строго обязателен.
Итак, выпишем область определения. С одной стороны, аргумент первого логарифма должен быть больше нуля:
С другой — второй аргумент тоже должен быть больше нуля:
Эти требования должны выполняться одновременно. И вот тут начинается самое интересное. Безусловно, мы можем решить каждое из этих неравенств, затем пересечь их и найти область определения всего уравнения. Но зачем так усложнять себе жизнь?
Давайте заметим одну тонкость. Избавляясь от знаков log, мы приравниваем аргументы. Отсюда следует, что требования x 2 − 6 x + 2 > 0 и 7 − 2 x > 0 равносильны. Как следствие, любое из двух неравенств можно вычеркнуть. Давайте вычеркнем самое сложное, а себе оставим обычное линейное неравенство:
x x = −1, потому что x = 5 > 3,5.
Можно записать ответ: x = 1 является единственным решением исходного логарифмического уравнения.
Выводы из данного логарифмического уравнения следующие:
Вот, собственно, и все, что я хотел рассказать о группировке.:)
Типичные ошибки при решении
Сегодня мы разберем два типичных логарифмических уравнения, на которых спотыкаются многие ученики. На примере этих уравнения мы увидим, какие ошибки чаще всего допускаются в процессе решения и преобразования исходных выражений.
Дробно-рациональные уравнения с логарифмами
Сразу следует отметить, что это довольно коварный тип уравнений, в которых отнюдь не всегда сразу присутствует дробь с логарифмом где-то в знаменателе. Однако в процессе преобразований такая дробь обязательно возникнет.
При этом будьте внимательны: в процессе преобразований изначальная область определения логарифмов может существенно измениться!
Переходим к еще более жестким логарифмическим уравнениям, содержащим дроби и переменные основания. Чтобы за один короткий урок успеть больше, я не буду рассказывать элементарную теорию. Сразу перейдем к задачам:
4 log25 ( x − 1) − log3 27 + 2 log x − 1 5 = 1
Посмотрев на это уравнение, кто-то спросит: «При чем здесь дробно-рациональное уравнение? Где в этом уравнении дробь?» Давайте не будем спешить и внимательно посмотрим на каждое слагаемое.
Итак, второе слагаемое — это просто тройка. Третье слагаемое: 2 log x − 1 5. Тут тоже не все просто: в основании стоит функция, в аргументе — обычное число. Предлагаю перевернуть весь логарифм по следующей формуле:
Такое преобразование можно выполнить только если b ≠ 1. Иначе логарифм, который получится в знаменателе второй дроби, просто не будет существовать. В нашем случае b = 5, поэтому все в порядке:
2 log x − 1 5 = 2/log5 ( x − 1)
Перепишем исходное уравнение с учетом полученных преобразований:
4 log25 ( x − 1) − 3 + 2/ log5 ( x − 1) = 1
Другими словами, степень в основании логарифма становится дробью спереди. А выражение перепишется так:
4 1/2 log5 ( x − 1) − 3 + 2/ log5 ( x − 1) − 1 = 0
У нас получилось длинное уравнение с кучей одинаковых логарифмов. Введем новую переменную:
А вот это уже дробно-рациональное уравнение, которое решается средствами алгебры 8—9 класса. Для начала разделим все на двойку:
В скобках стоит точный квадрат. Свернем его:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Никогда не забывайте про этот факт:
Вспоминаем, что такое t :
Избавляемся от знаков log, приравниваем их аргументы, и получаем:
С другой стороны, тот же x − 1 присутствует и в основании, поэтому должен отличаться от единицы:
Эти требования должны выполняться одновременно. Значение x = 6 удовлетворяет обоим требованиям, поэтому является x = 6 окончательным решением логарифмического уравнения.
Переходим ко второй задаче:
Вновь не будем спешить и посмотрим на каждое слагаемое:
log4 ( x + 1) — в основании стоит четверка. Обычное число, и его можно не трогать. Но в прошлый раз мы наткнулись на точный квадрат в основании, который пришлось выносить из-под знака логарифма. Давайте сейчас сделаем то же самое:
8 log x + 1 2 = 8 · (1/log2 ( x + 1)) = 8/log2 ( x + 1)
Следующее слагаемое — log2 8. Это константа, поскольку и аргументе, и в основании стоят обычные числа. Найдем значение:
То же самое мы можем сделать и с последним логарифмом:
Теперь перепишем исходное уравнение:
1/2 · log2 ( x + 1) + 8/log2 ( x + 1) − 3 − 1 = 0;
log2 ( x + 1)/2 + 8/log2 ( x + 1) − 4 = 0
Приведем все к общему знаменателю:
Перед нами опять дробно-рациональное уравнение. Введем новую переменную:
Перепишем уравнение с учетом новой переменной:
Будьте внимательны: на этом шаге я поменял слагаемые местами. В числителе дроби стоит квадрат разности:
Как и в прошлый раз, дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:
Получили один корень, который удовлетворяет всем требованиям, поэтому возвращаемся к переменной x :
Все, мы решили уравнение. Но поскольку в исходном уравнении присутствовало несколько логарифмов, необходимо выписать область определения.
Так, выражение x + 1 стоит в аргументе логарифма. Поэтому x + 1 > 0. С другой стороны, x + 1 присутствует и в основании, т.е. x + 1 ≠ 1. Итого:
Удовлетворяет ли найденный корень данным требованиям? Безусловно. Следовательно, x = 15 является решением исходного логарифмического уравнения.
Вот и все, о чем я хотел сегодня рассказать. Надеюсь, этот урок поможет вам в решении сложных логарифмических уравнений. Смотрите другие видеоуроки, скачивайте и решайте самостоятельные работы, и до встречи в следующем видео!
Логарифмы и их свойства
Обычно определение логарифма дают очень сложно и запутанно. Мы постараемся сделать это очень просто и наглядно.
Для того, чтобы разобраться, что такое логарифм, давайте рассмотрим пример:
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 (\(log_<2>(32)\)) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
Аналогично, глядя в таблицу получим, что:
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа \(b\) по основанию положительно числа \(a\) называется степень \(c\), в которую нужно возвести число \(a\), чтобы получить \(b\)
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
Или логарифм шести по основанию 4:
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм \(log_<4>(6)\). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6ке:
Значит \(log_<4>(6)\) принадлежите промежутку от 1 до 2:
Как посчитать логарифм
Почему так? Это следует из определения показательной функций. Показательная функция не может быть \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
Теперь давайте разберем общий алгоритм вычисления логарифмов:
Давайте разберем на примерах.
Пример 1. Посчитать логарифм \(9\) по основанию \(3\): \(log_<3>(9)\)
Пример 2. Вычислить логарифм \(\frac<1><125>\) по основанию \(5\): \(log_<5>(\frac<1><125>)\)
Пример 3. Вычислить логарифм \(4\) по основанию \(64\): \(log_<64>(4)\)
Пример 4. Вычислить логарифм \(1\) по основанию \(8\): \(log_<8>(1)\)
Пример 5. Вычислить логарифм \(15\) по основанию \(5\): \(log_<5>(15)\)
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\). Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
Натуральный логарифм
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой \(3\). Логарифм от произведения – это сумма логарифмов.
Пример 9. Воспользоваться формулой \(4\). Логарифм от частного – это разность логарифмов.
Пример 10. Формула \(5,6\). Свойства степени.
Логично, что будет выполняться и такое соотношение:
Пример 11. Формулы \(7,8\). Переход к другому основанию.