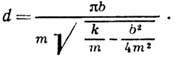Логарифмический декремент затухания в чем измеряется
Логарифмический декремент затухания в чем измеряется
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и 
(рис. 3.1):
,
где β – коэффициент затухания.
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
;
.
Выясним физический смысл χ и β.
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
отсюда 
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
; 
;
.
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Если χ = 0,01, то N = 100.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому 
, а 
то круговая частота обращается в нуль ( 
), а ( 
), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).
Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.
ДЕКРЕМЕНТ ЗАТУХАНИЯ
При малом затухании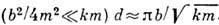 
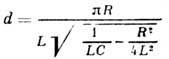
. Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.
.
При малом затухании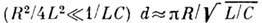 
.
Для нелинейных систем закон затухания колебаний отличен от закона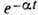 
, т. е. отношение двух последующих «амплитуд» (и логарифм этого отношения) не остаётся постоянным; поэтому Д. з. не имеет такого определ. смысла, как для систем линейных.
Полезное
Смотреть что такое «ДЕКРЕМЕНТ ЗАТУХАНИЯ» в других словарях:
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение) характеристика быстроты затухания колебаний: d = ln(A1/A2), где А1 и А2 амплитуды двух колебаний, следующих друг за другом в одну и ту же сторону … Большой Энциклопедический словарь
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (Decrement) величина, характеризующая постепенное затухание колебаний. Д. равен отношению двух амплитуд, следующих одна за другой через один период. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза… … Морской словарь
декремент затухания — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN damping decrement … Справочник технического переводчика
декремент затухания — (от лат. decrementum уменьшение), количественная характеристика быстроты затухания колебаний в линейной системе: Δ = ln(А1/А2), где А1 и А2 два последующих максимальных отклонения колеблющейся величины в одну и ту же сторону. * * * ДЕКРЕМЕНТ… … Энциклопедический словарь
декремент затухания — slopimo dekrementas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiantis virpesių amplitudės sumažėjimą per vieną periodą. atitikmenys: angl. damping ratio vok. Dämpfungsverhältnis, n rus. декремент затухания, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
декремент затухания — slopinimo dekrementas statusas T sritis automatika atitikmenys: angl. damping decrement; damping ratio vok. Dämpfungsbeiwert, m; Dämpfungsdekrement, n; Dämpfungsgrad, m; Dämpfungsverhältnis, n rus. декремент затухания, m; относительное затухание … Automatikos terminų žodynas
декремент затухания — slopimo dekrementas statusas T sritis automatika atitikmenys: angl. attenuation decrement; attenuation ratio vok. Dämpfungsgrad, m; Dämpfungsmaß, n rus. декремент затухания, m pranc. décrément d affaiblissement, m … Automatikos terminų žodynas
декремент затухания — slopinimo dekrementas statusas T sritis fizika atitikmenys: angl. damping decrement vok. Dämpfungsdekrement, n rus. декремент затухания, m pranc. décrément d’amortissement, m … Fizikos terminų žodynas
декремент затухания — rus коэффициент (м) звукопоглощения, коэффициент (м) затухания (звука); коэффициент (м) демпфирования; декремент (м) затухания eng damping coefficient, damping factor fra coefficient (m) d amortissement (m) deu Dämpfungsfaktor (m),… … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
Декремент затухания — количественная характеристика быстроты затухания колебаний. Д. з. δ равен натуральному логарифму отношения двух последующих максимальных отклонений х колеблющейся величины в одну и ту же сторону: Д. з. величина, обратная… … Большая советская энциклопедия
Логарифмический декремент затухания в чем измеряется
§6 Затухающие колебания
Декремент затухания. Логарифмический декремент затухания.
Добротность
Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.
Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.
Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r . По второму закону Ньютона
— дифференциальное уравнение затухающих колебаний.
— у равнение затухающих колебаний.
ω – частота затухающих колебаний:
Период затухающих колебаний:
Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно говорить, когда β мало.
Если затухания выражены слабо (β→0), то 
. Затухающие колебания можно
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз
Логарифмический декремент затухания равен логарифму D :
Еще одной характеристикой колебательной система является добротность Q .
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.
Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.
Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
§7 Вынужденные колебания.
Резонанс
В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.
По второму закону Ньютона:
(1)
— дифференциальное уравнение вынужденных колебаний.
Это дифференциальное уравнение является линейным неоднородным.
Его решение равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения:
Найдем частное решение неоднородного уравнения. Для этого перепишем уравнение (1) в следующем виде:
(2)
Частное решение этого уравнения будем искать в виде:
Это комплексное число удобно представить в виде
Его вещественная часть, являвшаяся решением уравнения (1) равна:
(3)
(4)
Слагаемое Хо.о. играет существенную роль только в начальной стадии при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения определяемого равенством (3). В установившемся режиме вынужденные колебания происходят с частотой ω и являются гармоническими. Амплитуда (3) и фаза (4) вынужденных колебаний зависят от частоты вынуждающей силы. При определенной частоте вынуждающей силы амплитуда может достигнуть очень больших значений. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте механической системы, называется резонансом.
Частота ω вынуждающей силы, при которой наблюдается резонанс, называется резонансной. Для того чтобы найти значение ωрез, необходимо найти условие максимума амплитуды. Для этого нужно определить условие минимума знаменателя в (3) (т.е. исследовать (3) на экстремум).
Зависимость амплитуды колеблющейся величины от частоты вынуждающей силы называется резонансной кривой. Резонансная кривая будет тем выше, чем меньше коэффициент затухания β и с уменьшением β, максимум резонансных кривых смешается вправо. Если β = 0, то
При ω→0 все кривые приходят к значению 
— статическое отклонение.
Логарифмический декремент затухания
Логарифмический декремент затухания
Величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний
Смотреть что такое «Логарифмический декремент затухания» в других словарях:
логарифмический декремент затухания — logaritminis slopinimo dekrementas statusas T sritis fizika atitikmenys: angl. logarithmic damping decrement vok. logarithmisches Dämpfungsdekrement, n rus. логарифмический декремент затухания, m pranc. décrément logarithmique d’affaiblissement,… … Fizikos terminų žodynas
логарифмический декремент колебаний — логарифмический декремент Ндп. логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях. Пояснения 1)Некоторые величины и… … Справочник технического переводчика
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение, убыль), количественная хар ка быстроты затухания колебаний. Д. з. d равен натуральному логарифму отношения двух последующих макс. отклонений х колеблющейся величины в одну и ту же сторону: d=ln(x1/x2). Д. з.… … Физическая энциклопедия
Логарифмический декремент колебаний — 107. Логарифмический декремент колебаний Логарифмический декремент Ндп. Логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях… … Словарь-справочник терминов нормативно-технической документации
ДЕКРЕМЕНТ ЗАТУХАНИЯ — логарифмический (от лат. decrementum уменьшениеубыль) количеств. хар ка затухания колебаний в линейной системе. Д. з. равен натур. логарифму отношения двух последовательных Макс. отклонений колеблющейся величины в одну и ту же сторону … Большой энциклопедический политехнический словарь
логарифмический декремент колебания тока — Характеристика затухания свободного колебательного тока, равная натуральному логарифму отношения двух последующих максимальных значений тока одного знака … Политехнический терминологический толковый словарь
декремент — (лат. decrementura убавление) 1) физ.д. затухания логарифмический величина, характеризующая степень ослабления затухающего колебательного процесса; д. равен логарифму отношения двух последующих амплитуд затухающего колебания; 2) физиол.… … Словарь иностранных слов русского языка
Переходной процесс — Переходный процесс в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных… … Википедия
Переходная характеристика — Переходный процесс в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных… … Википедия
Переходные процессы — Переходный процесс в теории систем представляет реакцию динамической системы на приложенное к ней внешнее воздействие с момента приложения этого воздействия до некоторого установившегося значения во временной области. Изучение переходных… … Википедия