Логарифмирование данных в статистике для чего
Логарифмирование данных в статистике для чего
Иногда данные нуждаются в преобразованиях. В частности, потребность в этом возникает, когда в ряду данных одно или несколько данных существенно превышают остальные. Если данные явно несимметричны, то заменяют каждое значение приведенного набора данных логарифмом этого значения с целью упростить статистический анализ. Логарифмирование преобразует «скошенные» (ассимметричные) данные в более симметричные, так как происходит «растягивание» шкалы возле нуля, малые значения, сгруппированные вместе, распределяются вдоль шкалы. В то же время логарифмирование собирает вместе большие значения на правом конце шкалы. Наиболее часто применяют десятичные и натуральные логарифмы. Равным расстояниям на логарифмической шкале соответствует на исходной шкале равные процентные увеличения, а не равные увеличения значений.
Пример. В таблице представлена численность населения (в тыс. чел.) в республиках бывшего СССР в 1976 г.
| Россия | Украина | Белоруссия | Узбекистан | Казахстан |
| 134650 | 49075 | 9371 | 14079 | 14337 |
| Грузия | Азербайджан | Литва | Молдавия | Латвия |
| 4954 | 5689 | 3315 | 3850 | 2497 |
| Киргизия | Таджикистан | Армения | Туркмения | Эстония |
| 3368 | 3486 | 2834 | 2581 | 1438 |
Заменим все значения их десятичными логарифмами. В нижеприведенной таблице вместо численности населения представлены их десятичные логарифмы.
| Россия | Украина | Белоруссия | Узбекистан | Казахстан |
| 8,13 | 7,69 | 6,97 | 7,15 | 7,16 |
| Грузия | Азербайджан | Литва | Молдавия | Латвия |
| 6,69 | 6,76 | 6,52 | 6,59 | 6,40 |
| Киргизия | Таджикистан | Армения | Туркмения | Эстония |
| 6,53 | 6,54 | 6,45 | 6,41 | 6,16 |
Как мы видим, данные симметрично группируются вокруг среднего значения 6,81.
Почему я пользуюсь логарифмической шкалой при просмотре графика цены акций?
Вводная заметка о пользе логарифмов.
Думаю, все вы понимаете, что конкретная цена акции не имеет никакого значения. Главное, чтобы её цена была не выше той суммы, которую инвестор хочет потратить. Например, акция BRK.A стоит порядка 420к$, что явно переходит все границы разумного. Но в остальном, если вы хотите купить акции какой-то компании на условные сотню баксов, то вам, в принципе, всё равно, будет ли это десять акций по десять долларов или сотня акций по доллару.
Значение имеет то, на сколько процентов цена изменилась. То, что какая-то акция поднялась на доллар — ничего вам не говорит, если вы не знаете, какая у неё была прошлая стоимость, потому что 1+1 и 10+1 — это совершенно разные вещи. С другой стороны, если акция поднялась на 25%, то вам совершенно не обязательно знать, сколько она стоила раньше — вы и так получили всю нужную информацию.
Допустим теперь, что вы анализируете поведение акции за большой временной период — несколько лет или даже десятилетий. Если компания развивалась всё это время, то цены сейчас намного выше цен более раннего периода. Например, акция TSLA совсем недавно стоила 900$, а несколько лет назад она стоила всего лишь 50$:
Если мы посмотрим на график выше, то колебания цены мы увидим только начиная с 2020 года. А начиная с 2014 года и до 2020 идет чуть ли не прямая линия, как будто цена акции все эти годы стояла на месте. Почему так? Потому что на фоне колебаний цены между 900$ и 550$, колебания между 30$ и 70$ совершенно не видны. А ведь в процентах второй случай куда как значимей.
А еще падение с 180$ до 70$ в начале 2020 года в процентах примерно в полтора раза сильнее падения с 900$ до 550$ в начале 2021 года, но на графике более позднее событие выглядит куда как страшнее более раннего.
Получается, что такой график не просто теряет часть информации, но и вводит нас в заблуждение.
Тут на помощь приходит логарифмическая шкала. Преимущество такой шкалы в её нелинейности. Я не буду объяснять, что такое логарифм — это вы можете сами в Википедии почитать. Да и, как известно, каждая дополнительная формула в статье уменьшает количество её читателей в два раза 🙂
На графике выше — та же акция, с тем же временным промежутком, но только в логарифмическом представлении. Сравните с прошлым, линейным графиком, и убедитесь, насколько понятней выглядит поведение цены за весь период времени, а не только за последний год.
Вообще говоря, кванты и алготрейдеры вовсю используют логарифмы, чтобы избавиться от «шума» в данных. Если я когда-нибудь найду достаточно времени, чтобы обучать алготрейдингу, то мы еще вернемся к этой теме.
Самостоятельно поиграться с логарифмическим представлением цен можно, к примеру, на TradingView, в настройках графика.
Если то, что я пишу, вам кажется интересным — подписывайтесь на мой телеграм-канал, чтобы своевременно получать уведомления о новых постах:
Поскриптум: я не инвестиционный консультант и никогда им не был. Ничто из вышенаписанного не следует рассматривать как инвестиционную рекомендацию.
Блог про HR-аналитику
Сделать репост в соц сети!
четверг, 12 февраля 2015 г.
Логарифмирование переменной: зачем это нужно и как интерпретировать
Это уже ближе к нормальному распределению.
И уравнение регрессии вы считаете для логарифмированной переменной.
Как интерпретировать
16 комментариев:
Эдуард, извините, я по своему примеру. Прологарифмировал стаж по натуральному основанию, распределение стало ближе к нормальному, коэф Колмогорова-Смирнова 0,308
я для вас и написал
и для Ивана
так теперь сделайте регрессионный анализ
пост для понимания ясно написан? или есть вопросы?
1) лог стаж
2) а какую информацию вы собираете при приеме на работу?
А что в лог-стаже вместо пропусков ставить. Или строим регрессию только по уволившимся?
сделайте по уволившимся. выбирайте только уволившихся и по ним делайте лог стажа
Максим, мне важно, чтобы вы сами делали, пробовали на вкус.
Появится опыт, уверенность
Эдуард, я имел ввиду закрывать переменную стаж на сегодняшнее число по тем, кто работает сейчас или оставлять пустой?
Максим, 1) попробуйте писать в одну ветку. 2) я не вижу ваших выводов
мне этого недостаточно
В линейной регрессии, когда уместно использовать лог независимой переменной вместо фактических значений?
Я ищу лучшее распределение для рассматриваемой независимой переменной, или чтобы уменьшить влияние выбросов или что-то еще?
Я всегда стесняюсь заходить в цепочку с таким большим количеством превосходных ответов, как это, но мне кажется, что лишь немногие из ответов дают какую-либо причину предпочесть логарифм другим преобразованиям, которые «сдавливают» данные, такие как корень или ответ.
Прежде чем перейти к этому, давайте подведем итоги мудрости в существующих ответах в более общем виде. Некоторое нелинейное повторное выражение зависимой переменной указывается, когда применимо любое из следующего:
Остатки имеют перекошенное распределение. Целью преобразования является получение остатков, которые приблизительно симметрично распределены (конечно, около нуля).
Разброс остатков систематически изменяется со значениями зависимой переменной («гетероскедастичность»). Цель трансформации состоит в том, чтобы устранить это систематическое изменение в распространении, достигнув приблизительной «гомоскедастичности».
Чтобы линеаризовать отношения.
Когда научная теория указывает. Например, химия часто предлагает выражать концентрации в виде логарифмов (давая активность или даже общеизвестный pH).
Когда более туманная статистическая теория предлагает, остатки отражают «случайные ошибки», которые не накапливаются аддитивно.
Упростить модель. Например, иногда логарифм может упростить количество и сложность терминов «взаимодействие».
(Эти признаки могут противоречить друг другу; в таких случаях требуется суждение.)
Итак, когда конкретно указывается логарифм вместо какого-либо другого преобразования?
Остатки имеют «сильно» положительно перекошенное распределение. В своей книге об EDA Джон Тьюки предоставляет количественные способы оценки трансформации (в пределах семейства Бокса-Кокса, или силовых трансформаций) на основе ранговых статистик невязок. Это действительно сводится к тому факту, что если взятие логарифма симметрирует остатки, это, вероятно, была правильная форма повторного выражения; в противном случае необходимо другое выражение.
Когда SD остатков прямо пропорционально установленным значениям (а не какой-то степени установленных значений).
Когда отношения близки к экспоненциальным.
Когда считается, что остатки отражают мультипликативно накапливающиеся ошибки.
Вы действительно хотите модель, в которой предельные изменения в объясняющих переменных интерпретируются как мультипликативные (процентные) изменения в зависимой переменной.
И, наконец, некоторые не- причины использовать повторное выражение :
Потому что программное обеспечение автоматически сделало это. (Достаточно сказано!)
Потому что все данные положительные. (Позитивность часто подразумевает положительную асимметрию, но это не обязательно. Более того, другие преобразования могут работать лучше. Например, корень часто лучше всего работает с подсчитанными данными.)
Чтобы «плохие» данные (возможно, низкого качества) выглядели хорошо.
Я всегда говорю студентам, что есть три причины для преобразования переменной, взяв натуральный логарифм. Причина регистрации переменной будет определять, хотите ли вы зарегистрировать независимую переменную (переменные), зависимую или обе. Чтобы было ясно, я говорю о натуральном логарифме.
Во-первых, для улучшения подгонки модели, как отмечали другие постеры. Например, если ваши остатки обычно не распределяются, то взятие логарифма перекошенной переменной может улучшить подгонку, изменив масштаб и сделав переменную более «нормально» распределенной. Например, доход усекается до нуля и часто демонстрирует положительный перекос. Если переменная имеет отрицательный перекос, вы можете сначала инвертировать переменную, прежде чем брать логарифм. Я имею в виду, в частности, шкалы Лайкерта, которые вводятся как непрерывные переменные. Хотя это обычно относится к зависимой переменной, иногда возникают проблемы с остатками (например, гетероскедастичностью), вызванными независимой переменной, которые иногда можно исправить, взяв логарифм этой переменной. Например, при запуске модели, объясняющей оценки лектора на наборе лектора и класса, переменная «размер класса» (т. Е. Количество студентов в лекции) имела выбросы, которые вызывали гетероскедастичность, потому что дисперсия в оценках лектора была меньше в большем когорты, чем меньшие когорты. Регистрация переменной студента может помочь, хотя в этом примере либо расчет робастных стандартных ошибок, либо использование взвешенных наименьших квадратов может облегчить интерпретацию.
И, наконец, может быть теоретическая причина для этого. Например, некоторые модели, которые мы хотели бы оценить, являются мультипликативными и, следовательно, нелинейными. Взятие логарифмов позволяет оценивать эти модели с помощью линейной регрессии. Хорошие примеры этого включают производственную функцию Кобба-Дугласа в экономике и уравнение Минцера в образовании. Производственная функция Кобба-Дугласа объясняет, как входы преобразуются в выходы:
Принятие логарифмов этого упрощает оценку функции с использованием линейной регрессии OLS как таковой:
Логарифмический график
Хочу рассказать об одной важной вещи, которую должен знать каждый начинающий инвестор.
Сразу скажу, что когда я сам начинал инвестировать, я не знал об этом. Речь идет о логарифмическом графике, позволяющем объективно оценить долгосрочный рост активов.
Приведу определение логарифмического графика из Википедии:
«Логарифмический масштаб (шкала) — шкала, длина отрезка которой пропорциональна логарифму отношения величин, отмеченных на концах этого отрезка, в то время как на шкале в линейном масштабе длина отрезка пропорциональна разности величин на его концах»
Если вы не учились на физ-мате, для вас это наверняка звучит как полная белиберда, собственно, как и для меня. Поэтому объясню своими словами.
Есть два вида графиков: линейный и логарифмический.
Первый вы все знаете: у него вертикальная шкала растет линейно, например, 0, 10, 20, 30, 40 и т.д. Т.е. шкалу задает величина между нулем и первым значением (абсолютный прирост в единицах, в примере – 10 единиц).
Со вторым интереснее: здесь рост нелинейный (геометрический), например, 0, 10, 20, 40, 80 и т.д. Тут шкалу задает относительный (процентный) прирост. В моем примере это рост в каждом периоде на 100%.
Разница в том, что логарифмический график более адекватно показывает относительный прирост. Т.е. в моем примере выше с логарифмическим графиком каждый год (пусть 0 — цена в первый год, 10 — во второй, 20 — в третий и т.д.) цена росла на 100%. И на графике это будет прямой трендовой линией.
Если этот же актив поместить на линейный график, то сначала будет казаться, что он почти не растет, а к концу мы увидим невероятный рост. Будет складываться ощущение, что актив перекуплен и вот-вот должен рухнуть.
Чтобы наглядно это увидеть я привел несколько сравнений линейных и логарифмических графиков одних и тех же активов. Я взял данные по S&P 500, Татнефти и Новатэку и McDonald’s из Investing.com.
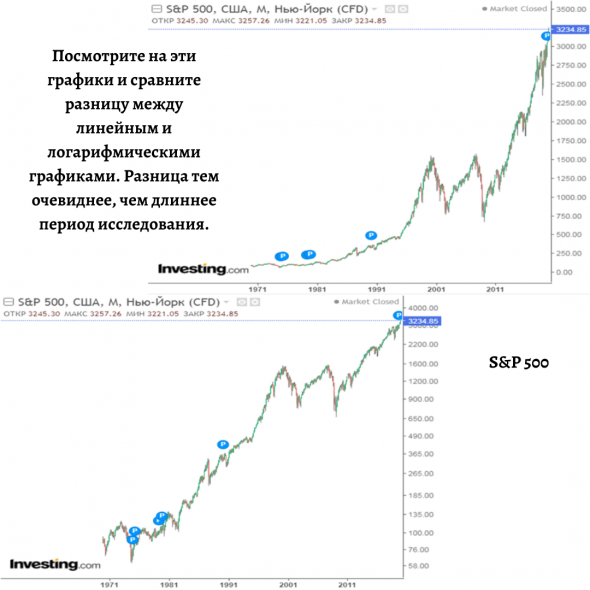
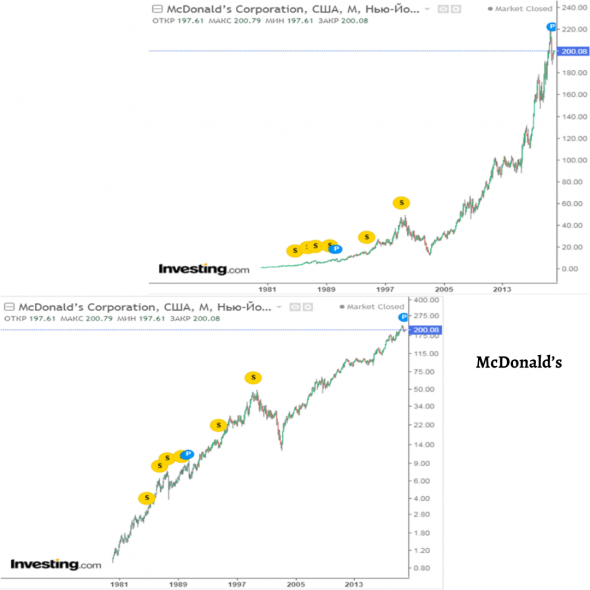
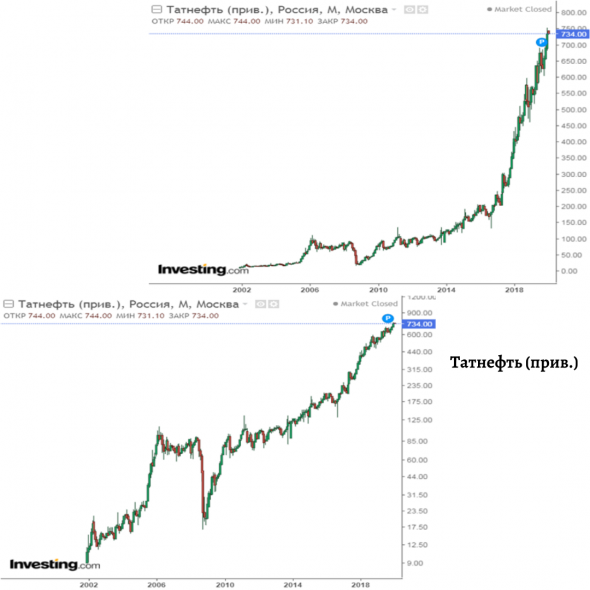
Если на графиках Татнефти и Новатэка эффект выражен не так сильно ввиду недолгого периода существования Московской биржи (хотя тоже существенен), то на американских графиках (S&P 500 и McDonald’s) разница очевидна. Посмотрите на McDonald’s: на линейном графике кажется, как будто люди с ума сошли: покупают невероятно выросший актив. В то же время складывается ощущение, что раньше McDonald’s вообще не рос и не представлял инвестиционной привлекательности (до 1990 года).
Если же посмотреть на логарифмический график McDonald’s, то мы увидим, что сейчас темп роста, наоборот, замедлился в процентном отношении. Именно этот график показывает правдивую картину. McDonald’s давно уже стал зрелой компанией, и он физически не может расти быстрее, потому что и так занимает огромную долю рынка. Он может только поддерживать стабильный, устойчивый рост.
Поэтому если вы придерживаетесь, что называется, long-term investments, т.е. долгосрочных инвестиций, то обязательно смотрите на логарифмический график, чтобы объективно оценить тренд и темпы роста цен на активы на длинных периодах времени.