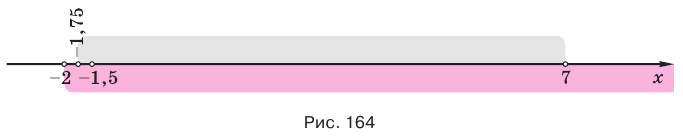
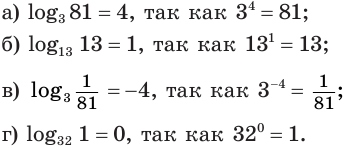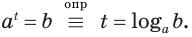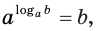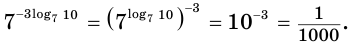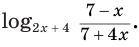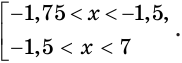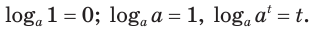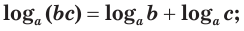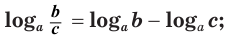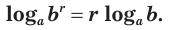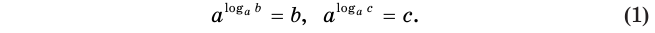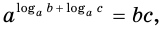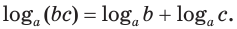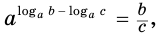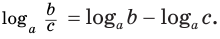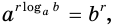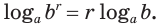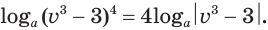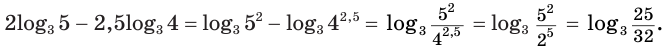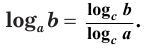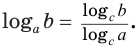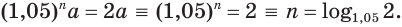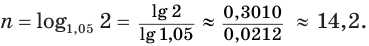Логарифмируемое выражение что это
Что такое логарифм. Как посчитать логарифм. Свойства логарифмов. Примеры решения логарифмов
Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выражения


Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выражения
Теперь применим переход к новому основанию для второго логарифма:
10 примеров логарифмов с решением
1. Найти значение выражения















10. Найти значение выражения
Надеюсь, теперь вы разобрались, что такое логарифм.
Логарифмические выражения с примерами решения
Мы уже умеем по значению
Пример:
Решим уравнение 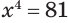
Теперь поставим задачу нахождения показателя 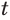
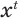
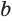
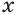
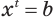
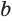
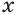
Пример:
Решим уравнение 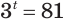
Это уравнение можно записать как 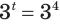
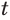
Обратим внимание на то, что при решении уравнения 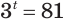
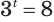
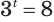
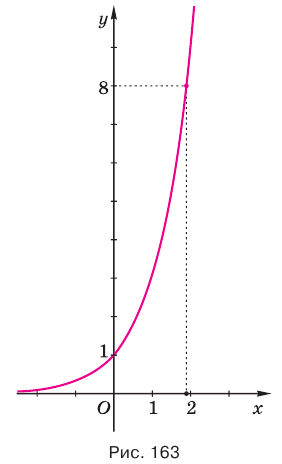
Этот корень называют логарифмом числа 8 по основанию 3 и обозначают 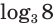
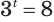
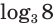
Логарифмом числа 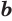
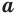
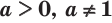
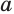
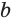
Логарифм числа 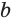
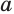
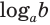
Пример:
Таким образом, учитывая определение логарифма числа, корень уравнения 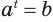
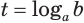
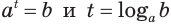
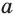
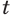
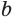
Пример:
Решим уравнение 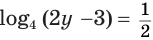
Определение логарифма позволяет данное уравнение заменить равносильным уравнением 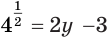
Определение логарифма коротко можно представить равенством
которое называют основным логарифмическим тождеством.
Пример:
Вычислим значение выражения 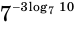
Используем свойство возведения степени в степень и основное логарифмическое тождество:
Из свойств показательной функции следует, что выражение 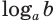
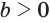
Пример:
Найдем область определения выражения
Данное выражение имеет значение, если основание логарифма 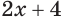
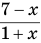
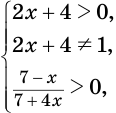
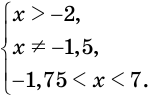
Из определения логарифма следует, что
Действие нахождения логарифма числа называется логарифмированием.
Введение действия логарифмирования порождает новый класс логарифмических выражений, т. е. выражений, которые содержат по крайней мере одно действие нахождения логарифма из выражения с переменной. При преобразованиях логарифмических выражений используются свойства действия логарифмирования. Установим эти свойства.
Теорема 5.
При любом положительном и не равном единице основании:
логарифм произведения положительных множителей равен сумме их логарифмов:
логарифм частного с положительными делимым и делителем равен разности логарифмов делимого и делителя:
логарифм любой действительной степени положительного числа равен произведению показателя степени и логарифма основания:
Доказательство:
Пусть 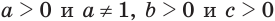
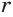
Основное логарифмическое тождество позволяет записать равенства:
Перемножив их, получим:
откуда, по определению логарифма:
Если разделить первое равенство из (1) на второе, то получим, что
откуда, по определению логарифма:
Возведя первое равенство из (1) в степень с показателем 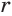
откуда, по определению логарифма:
Обращаем внимание на то, что при применениях тождеств, установленных теоремой 5, нужно следить за тем, чтобы все подлогарифмические выражения были положительными.
Пример:
а) 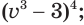
а) Получим
б) Выражение 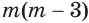
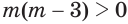
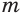
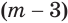
Если оба множителя 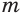
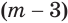
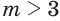
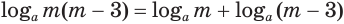
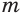
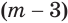
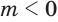
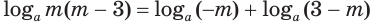
Действие, обратное логарифмированию, называют потенцированием.
Пример:
Пропотенцируем выражение 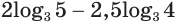
Будем последовательно получать:
Логарифмы чисел находят с помощью специальных таблиц или калькулятора. И в том, и в другом случае находят десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10.
Для десятичного логарифма вместо 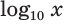
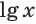
Для натурального логарифма вместо 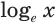
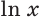
Для вычислений достаточно иметь возможность находить логарифмы по одному основанию, так как тогда можно найти логарифм числа по другому основанию. Это позволяет делать формула перехода к другому основанию.
Теорема 6.
Логарифм числа по данному основанию равен логарифму числа по новому основанию, деленному на логарифм данного основания по новому основанию:
Доказательство:
Пусть 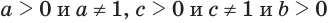
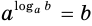
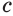
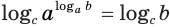
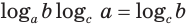
Пример:
Найдем, через сколько лет удвоится пятипроцентный вклад в банк.
Пусть имеется вклад в 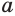
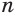
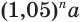
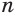
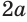
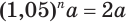
Вычисления проведем с помощью калькулятора, на котором есть клавиша для нахождения десятичных логарифмов:
Таким образом, удвоение пятипроцентного вклада произойдет через 14,2 года.
Открытие логарифмов было вызвано в XVI в. быстрым развитием астрономии и усложнением астрономических вычислений, которые имели непосредственное практическое значение при определении местонахождения судов по Солнцу и другим звездам. Логарифмы быстро вошли в практику.
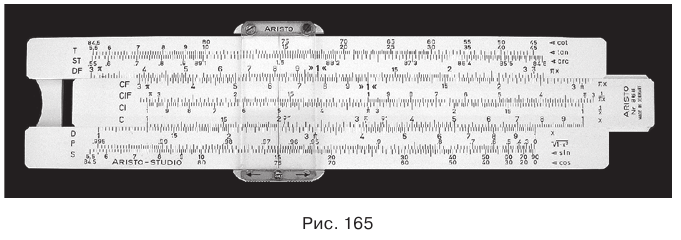
Первые логарифмические таблицы были составлены в одно время и независимо друг от друга шотландским математиком Джоном Непером (1550—1617) и швейцарским математиком и астрономом Йобстом Бюрги (1552—1632). В 1623 г. английский математик Эдмунд Гантер изобрел логарифмическую линейку, с помощью которой действия над числами — умножение, деление — заменяются действиями сложения и вычитания над логарифмами этих чисел. На рисунке 165 показана одна из логарифмических линеек. Сейчас нужные вычисления проводятся с помощью калькуляторов. Леонард Эйлер (1707—1783) установил, что действие логарифмирования является обратным действию возведения в степень. Термин логарифм предложен Джоном Непером. Современное определение логарифма впервые дано в 1742 г. английским математиком Вильямом Гардинером.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.