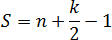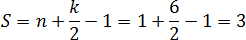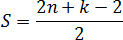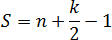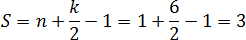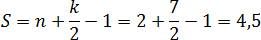Ломаная с вершинами в узлах сетки что это
Страница 15 №21-26 ГДЗ к учебнику «Математика» 5 класс Бунимович, Дорофеев, Суворова
Ломаная
Задание 21. Перечертите в тетрадь ломаную (рис.1.20). Запишите ее звенья.
Решение
У ломаной ABCD 3 звена: AB, BC, CD.
Задание 22. а) Постройте в тетради ломаную по следующему описанию:
• отметьте в одном из узлов квадратной сетки точку A;
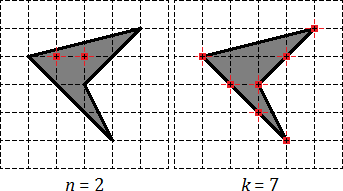
• от точки A отсчитайте 7 клеток влево и 1 клетку вниз, отметьте точку B;
• от точки B отсчитайте 5 клеток вправо и 3 клетки вниз, отметьте точку C;
• от точки C отсчитайте 3 клетки вправо и 6 клеток вверх, отметьте точку O.
Соедините точки по линейке в том порядке, в котором вы их строили. Назовите ломаную. Из скольких звеньев она состоит?
б) Начертите в тетради какую−нибудь ломаную с вершинами в узлах сетки и «продиктуйте» ее соседу по парте.
Решение
а)
Ломаная ABCO состоит из трех звеньев: AB, BC, CO.
б) 
• отметьте в одном из узлов квадратной сетки точку A;
• от точки A отсчитайте 5 клеток влево и 2 клетки вниз, отметьте точку B;
• от точки B отсчитайте 7 клеток вправо и 4 клетки вниз, отметьте точку C;
• от точки C отсчитайте 2 клетки вправо и 2 клетки вверх, отметьте точку D.
Ломаная ABCD состоит из трех звеньев: AB, BC, CD.
Задание 23. Начертите в тетради:
а) замкнутую ломаную, состоящую из трех звеньев;
б) незамкнутую ломаную, состоящую из четырех звеньев.
Решение
а)
Ломаная ABC состоит из трех звеньев: AB, BC, AC.
б)
Ломаная ABCDE состоит из четырех звеньев: AB, BC, CD, DE.
Задание 24. Отметьте и обозначьте три точки, не лежащие на одной прямой. Сколько можно построить незамкнутых ломаных с вершинами в этих точках?
Указание.
Для каждого случая сделайте рисунок.
Решение
Всего можно провести 3 незамкнутые ломаные:
Задание 25. На рисунке 1.21 изображен каркас куба. Назовите:
а) отрезки, одним из концов которых является точка M;
б) какую−нибудь ломаную, состоящую из трех звеньев;
в) несколько ломаных, по которым можно пройти из точки A в точку K.
Какой путь короче: ABKM или ABCDNM? Назовите еще какой−нибудь путь такой же длины, что и ABKM, и путь такой же длины, что и ABCDNM.
Решение
а) CM, NM, KM.
б) Ломаная ADNM состоит из 3 звеньев: AD, DN, NM.
в) ALNMK, ADCBK, ADNMCBK.
Путь ABKM короче, так как в нем 3 звена, а в пути ABCDNM 5 звеньев.
Путь ALND такой же длины что и ABKM.
Путь ADNLKM такой же длины что и ABCDNM.
Задание 26. ЗАДАЧА−ИССЛЕДОВАНИЕ
1) Начертите две пересекающиеся прямые. Проведите третью прямую, пересекающую каждую из этих прямых и не проходящую через их точку пересечения. Сколько точек попарного пересечения прямых у вас получилось?
2) В некотором городе три попарно пересекающиеся улицы. На каждом перекрестке установлен светофор. Сколько всего светофоров в городе? Было решено проложить новую улицу, пересекающую все старые и не проходящую через уже имеющиеся перекрестки. Сколько придется установить светофоров? А если прокладка улиц будет продолжена таким же образом, можно ли сказать, сколько будет светофоров в городе с десятью улицами?
Решение
1)
Получилось 3 точки попарного пересечения прямых: A, B, C.
2)
Так как улицы пересекаются попарно, то на них стоит три светофора.
Прокладываем четвертую улицу так, чтобы она не проходила ни через один перекресток, она пересекает все три имеющиеся улицы, поэтому придется добавить еще 3 светофора.
Метод узлов
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
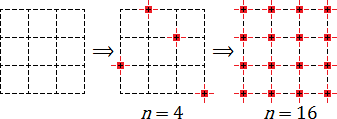
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
Задача:
Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
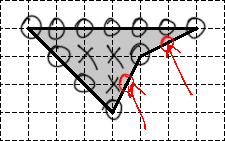
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача 2:
Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
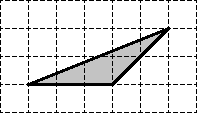
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
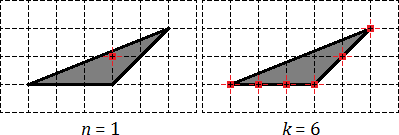
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача 3:
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
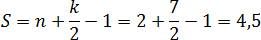
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
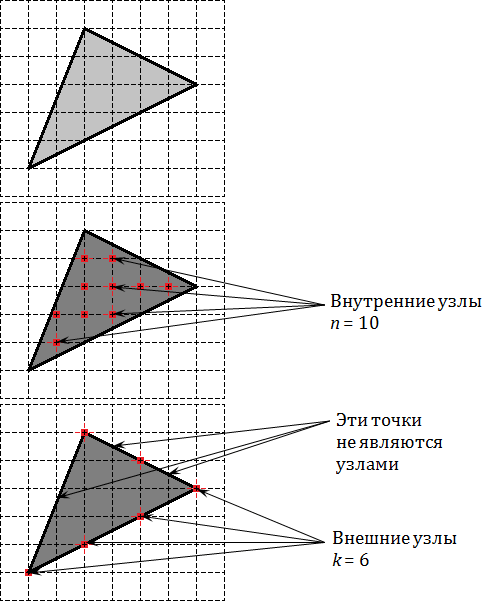
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»:
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Сегодня мы научились считать площади фигур в задаче B5 методом узлов. Повторим, что для начала введят два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5
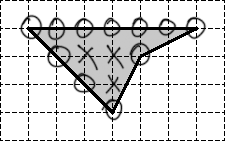
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Крестиками обозначены внутренние узлы. Очевидно, их количество Кружками обозначены граничные узлы. Их общее количество равно
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Теорема. Пусть дана фигура с внутренними узлами и граничными узлами. Тогда площадь этой фигуры считается по формуле:
S = n + 0,5 k − 1
Вот так все просто! Главное — запомните, это число внутренних узлов, число граничных узлов.
В нашем случае мы уже подсчитали, что Подставляем полученные числа в формулу и получаем:
Мы получили ответ: площадь четырехугольника
Ответ: 7,5
Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.
Метод узлов в задаче B5
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Страница 11 №15-21 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова
1. 2 Прямая. Части прямой. Ломаная
Решение
Через одну точку можно провести бесконечное множество прямых.
C началом в точке D 6 лучей: DA, DB, DC, DE, DF, DG.
Задание № 16. Отметьте в тетради точки A и C. Проведите через них прямую. Отметьте точку B, лежащую на прямой AC, и точку K, не лежащую на прямой AC. Проведите луч с началом в точке K, пересекающий отрезок AB.
Задание № 17. Рассмотрите рисунок 1. 15. и скажите, верно ли утверждение:
1) Точка A лежит на отрезке BC.
2) Точка A лежит на луче BD.
3) Точка D не лежит между точками A и C.
4) Точки D и C лежат на одном и том же луче с началом в точке B.
Решение
Задание № 18. Проведите прямую и отметьте на ней точки A и B. Отметьте на прямой AB точку C так, чтобы она принадлежала отрезку AB; точку D так, чтобы она не принадлежала отрезку AB.
Задание № 19. Перечертите в тетрадь ломаную (рис. 1. 16). Запишите её звенья.
Решение
Звенья ломаной: AB, BC, CD.
Задание № 20. 1) Что такое алгоритм? Найдите в словаре значение этого слова.
2) Постройте в тетради ломаную по следующему алгоритму:
Шаг 1. Отметьте в одном из узлов квадратной сетки точку A.
Шаг 2. От точки A отсчитайте 7 клеток влево и 1 клетку вниз. Отметьте точку B.
Шаг 3. От точки B отсчитайте 5 клеток вправо и 3 клетки вниз. Отметьте точку C.
Шаг 4. От точки C отсчитайте 3 клетки вправо и 6 клеток вверх. Отметьте точку O.
Шаг 5. Соедините точки по линейке в том порядке, в котором вы их строили.
3) Начертите в тетради ломаную с вершинами в узлах сетки и продиктуйте её соседу по парте. Сравните построенные с вами ломаные.
Решение
Алгоритм − последовательность операций.
Задание № 21. Начертите в тетради:
а) замкнутую ломаную, состоящую из трёх звеньев;
б) незамкнутую ломаную, состоящую из четырёх звеньев.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии