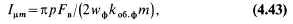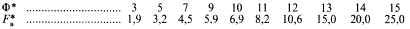Магнитная характеристика машины постоянного тока

Магнитная характеристика машины

Суммировав вычисленные МДС участков магнитной цепи для номинального магнитного потока , получим номинальную МДС возбуждения на пару полюсов:

(1.45)

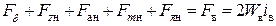
Повторив расчёт для ряда значений :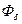

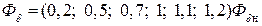
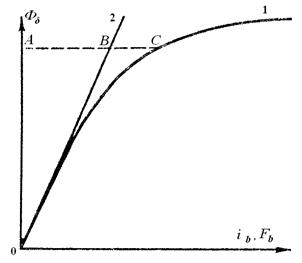
(1.46)

можно построить магнитную характеристику (кривую намагничивания) машины (рис. 1.15).

Рис. 1.15. Магнитная характеристика:

(1) – кривая намагничивания машины;

(2) – ненасыщенная характеристика

Если провести касательную к основной кривой намагничивания, то получим ненасыщенную характеристику, и можно определить коэффициент насыщения:

. (1.47)

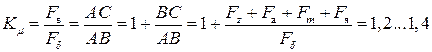
Здесь АВ = F_δ – МДС, расходуемая на создание и проведение потока через воздушный зазор;

– сумма МДС, расходуемая на создание и проведение потока через ферромагнитные участки магнитопровода.

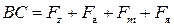
Проектировать машину с ненасыщенной магнитной цепью невыгодно, т.к. материалы будут недоиспользованы, но нецелесообразно и проектировать машину с очень насыщенной магнитной цепью, т.к. в этом случае МДС возбуждения велика и необходимо выполнить мощную обмотку возбуждения с большим расходом меди и с большими потерями на возбуждение. Таким образом, рабочая точка 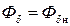должна лежать на перегибе магнитной характеристики.

Дата добавления: 2014-12-09 ; просмотров: 1132 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Магнитная характеристика машин постоянного тока

Определить намагничивающую силу цепи и построить зависимость намагничивающей силы цепи и магнитного потока машины постоянного тока можно после того, как будет рассчитано магнитное сопротивление всех участков магнитной цепи.

Построим кривую намагничивания машины, которая повторяет намагничивающую кривую стали.

Магнитную характеристику можно разделить на 3 участка:

I — линейный. На этом участке магнитная цепь машины не насыщена, и единственное сопротивление прохождению магнитного потока оказывает воздушный зазор.

II — нелинейный (рабочий) участок. Работа на этом участке экономически выгодна, а главное достоинство, что на этом участке можно регулировать магнитный поток.

III — область насыщения — участок, на котором изменение тока в обмотке возбуждения не приводит к изменению магнитного потока. Попадание машины в область насыщения нежелательно.

Правильность расчета магнитной цепи проверяется коэффициентом насыщения магнитной цепи.

Его можно определить графически по магнитной характеристике машины, отложив номинальный магнитный поток и продлив линейный участок.

Если коэффициент насыщения K_μ будет меньше 1.2, это будет значить, что машина будет не насыщена.

Если K_μ > 1.35, то машина перенасыщена, у ней большое магнитное сопротивление, машина будет греться при работе.

Источник

МАГНИТНОЕ ПОЛЕ МАШИНЫ ПОСТОЯННОГО ТОКА

Режим холостого хода. Магнитный поток при холостом ходе в машине создается только МДСFв обмотки возбуждения. В этом случае магнитный поток Ф_в при симметричном воздушном зазоре между якорем и сердечником главного полюса распределяется симметрично относительно продольной оси машины (рис. 8.21).

Зависимость магнитного потока возбуждения Ф_в от МДС F_в (магнитная характеристика — рис. 8.22) для машин постоянного тока подобна магнитной характеристике для синхронных машин. Однако при проектировании машин постоянного тока допускают большие индукции на участках магнитной цепи (в зубцах, якоре, станине и полюсах), чем в синхронных машинах, вследствие чего для них коэффициент насыщения k_нас = F/F_δ = ab/ac = 1,2 ÷ 2. Расчет магнитной цепи машины постоянного тока производят так же, как и для машин переменного тока (см. § 3.7).

Реакция якоря. При работе машины под нагрузкой по обмотке якоря проходит ток, вследствие чего возникает МДС якоря. Воздействие МДС якоря на магнитное поле машины называют реакцией якоря. Для упрощения анализа явления реакции якоря будем пренебрегать насыщением магнитной цепи машины и считать, что МДС F_в обмотки возбуждения и МДС F_aqобмотки якоря расходуются на преодоление магнитными потоками воздушного зазора. В этом случае вместо указанных МДС можно рассматривать соответствующие потоки: возбуждения Ф_в и реакции якоря Ф_aq .

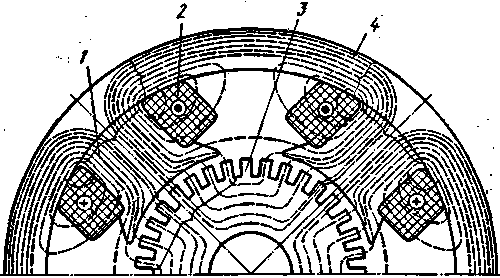Рис. 8.21. Магнитное поле машины постоянного тока в режиме холостого хода: 1 — полюс; 2 — обмотка возбуждения; 3 — якорь; 4 — корпус (станина)

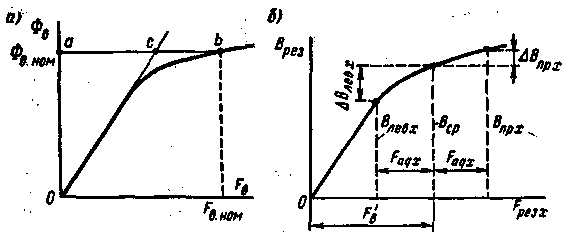Рис.8.22. Магнитная характеристика машины постоянного тока (а) и графикдля определения размагничивающего действия поперечного поля реакции якоря (б)

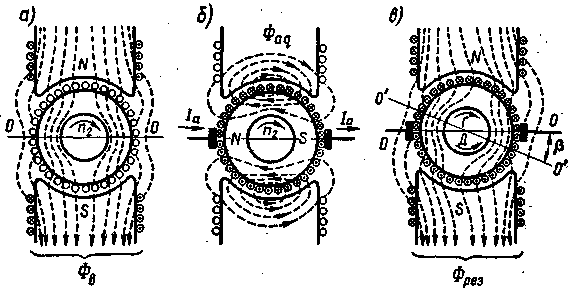Рис. 8.23. Характер магнитного поля машины постоянного тока,: создаваемые обмоткой возбуждения (а), обмоткой якоря (б)и результирующего поля (в)

Чтобы построить кривую В_рез = f(х) распределения результирующей индукции вдоль окружности якоря, применим метод суперпозиции. Его можно использовать, если пренебречь насыщением магнитной цепи машины и считать, что МДС F_в и F_aq расходуются на компенсацию разности магнитных потенциалов в воздушном зазоре. Так как обмотка возбуждения является сосредоточенной, то кривая распределения создаваемой ею МДС F’_в =f(x) имеет форму прямоугольника, где F’_в = 0,5F_в — МДС, приходящаяся на один воздушный зазор. В этом случае кривая индукции В_в = f(x) имеет форму криволинейной трапеции (рис. 8.24, а).

Для построения кривой МДС F_aqx = f(x) и создаваемой ею индукции B_aqx =f(x) примем,

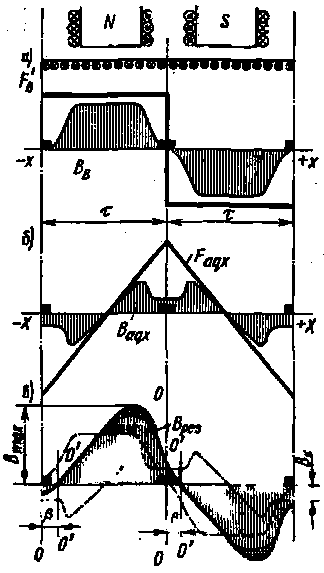Рис. 8.24. Кривые распределения индукции в воздушном зазоре машины постоянного тока

что обмотка якоря равномерно распределена по его окружности. Тогда на основании закона полного тока МДС якоря, действующая вдоль контура обхода через точки воздушного зазора на расстояния х от оси главных полюсов,

а МДС, приходящаяся на один зазор,

Следовательно, МДС якоря F_aqxизменяется линейно вдоль его окружности (рис. 8.24, б); под серединой главного полюса она равна нулю, а в точках, где установлены щетки, имеет максимальное значение. При ненасыщенной магнитной системе магнитная индукция в воздушном зазоре

где δ_x — величина воздушного зазора в точке х.

Кривую распределения результирующей индукции В_рез = f(x) можно получить алгебраическим сложением ординат кривых B_в = f(x) и
B_aqx = f(x). Как видно из рис. 8.24, в, эта кривая имеет пики индукции В_max под краями главных полюсов.

Если машина работает при небольших токах возбуждения, т. е. на прямолинейной части (машина не насыщена), то реакция якоря размагничивающего действия не оказывает. Аналогичный эффект получается и при значительном насыщении, когда машина снова работает на прямолинейном участке магнитной характеристики.

Рис. 8.25. Схемы возникновения продольной (а) и поперечной (б) МДС якоря при сдвиге щеток с геометрической нейтрали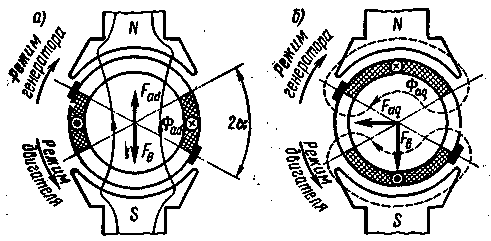

Продольная МДС Ф_aq создает продольный поток Ф_ad , который может сильно увеличивать или уменьшать результирующий магнитный поток машины Ф_рез в зависимости от того, совпадает МДС F_aq с F_в или направлена против нее. Направление определяется тем, в какую сторону сдвинуты щетки. Если щетки сдвинуты по направлению вращения генератора или против направления вращения электродвигателя, то продольная МДС F_ad размагничивает машину. При сдвиге щеток в обратном направлении МДС F_ad подмагничивает машину. Свойство продольной МДС F_ad изменять результирующий магнитный поток Ф_рез используется в некоторых специальных машинах, например в электромашинных усилителях с поперечным полем. Поперечная МДС F_aq создает магнитный поток Ф_aq ; она действует на поток Ф_рез так же, как и при расположении щеток на геометрической нейтрали.

Источник

Магнитная характеристика электрических машин

Если магнитный поток машины создается обмоткой возбуждения, питаемой постоянным током, то необходимый ток возбуждения определяется по известному значению МДС величины FB на пару полюсов:

где wB — число витков обмотки возбуждения.

При создании магнитного потока многофазной обмоткой, питаемой переменным током, амплитуда намагничивающего тока в фазе

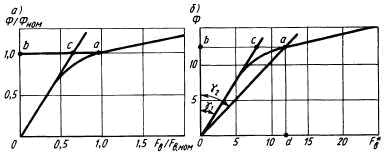
Рис. 4.34. Магнитные характеристики электрических машин

где wф и kоб.ф — число витков в фазе и обмоточный коэффициент данной обмотки; т — число фаз.

Действующее значение намагничивающего тока

где kμ — коэффициент, зависящий от степени насыщения магнитной системы (при ненасыщенной машине kμ = 0,707; по мере насыщения коэффициент уменьшается до значений kμ = 0,5. 0,4).

На рис. 4.34, а приведена типичная магнитная характеристика Ф = f(FB) в относительных единицах для электрических машин с явновыраженными полюсами (синхронных машин и машин постоянного тока). Ее можно построить по результатам расчета магнитной системы машины при различных значениях магнитного потока. На магнитной характеристике резко выражен начальный прямолинейный участок, что обусловлено наличием сравнительно большого воздушного зазора, для которого характерна линейная зависимость магнитного напряжения от магнитного потока Ф. При сравнительно малых значениях магнитного потока, а следовательно, и магнитной индукции в ферромагнитных участках магнитной системы магнитными напряжениями на этих участках можно пренебречь и считать, что FB ≈ Fδ. По мере увеличения магнитного потока магнитные сопротивления стальных участков возрастают, особенно сильно зубцового слоя. При индукции в зубцах, примерно равной 1,6 Тл, зависимость Ф = f(FB) начинает отклоняться от прямолинейной.

В большинстве электрических машин точку a, соответствующую номинальному режиму, выбирают на криволинейном участке магнитной характеристики. При работе на линейном участке (т. е. при небольшой магнитной индукции) плохо используется сталь магнитной системы, а при больших насыщениях резко возрастает МДС обмотки, создающей магнитный поток, следовательно, число витков этой обмотки и поперечное сечение провода. Таким образом, ненасыщенная машина и машина с большим насыщением магнитной системы требуют повышенного расхода активных материалов.

Количественно степень насыщения магнитной системы характеризуется коэффициентом насыщения kнас, которых можно найти из магнитной характеристики (рис. 4.34, а) как отношение отрезка ab, соответствующего МДС Fв.ном, к отрезку be, отсекаемому продолжением прямолинейного участка магнитной характеристики. Для машин переменного тока kнас = 1,1. 1,3; для машин постоянного тока kнac = 1,4. 1,8. Применение несколько меньших коэффициентов насыщения в синхронных машинах по сравнению с машинами постоянного тока объясняется стремлением уменьшить магнитные потери в стали якоря и сократить число витков обмотки возбуждения.

Магнитные характеристики различных машин с одинаковыми коэффициентами насыщения, выраженные в относительных единицах, практически совпадают. Это означает, что все многообразие магнитных характеристик можно свести к одной кривой, выраженной в некоторых условных единицах. Такая универсальная кривая, полученная из магнитной характеристики реальной машины, изображена на рис. 4.34,б и соответствует приведенным ниже цифрам:

Если требуется построить магнитную характеристику для машины, имеющей, например, kнас = 1,5, то поступают следующим образом. На универсальной магнитной характеристике (рис. 4.34, б) из начала координат проводят вспомогательную прямую, образующую с осью ординат угол γ2, тангенс которого в 1,5 раза больше тангенса угла γ1, образуемого прямолинейной частью универсальной магнитной характеристики с той же осью. Вспомогательная прямая пересекает универсальную характеристику в точке а, которая и соответствует номинальному режиму, т. е. в данном случае Ф*ном = 12,3 (точка b) и F*в.ном = 11,85 (точка d).

В соответствии с полученными значениями Φ*ном и F*в.ном можно перестроить универсальную магнитную характеристику в характеристику, выраженную в относительных единицах с kнас = 1,5, используя формулы Ф/Фв.ном = Ф*/Фв.ном и Fв/Fв.ном = F*в/F*в.ном. Построенные таким способом расчетные кривые дают погрешность не более 3%.

Источник

Магнитная характеристика машины

Суммировав вычисленные МДС участков магнитной цепи для номинального магнитного потока , получим номинальную МДС возбуждения на пару полюсов:

(1.45)

Повторив расчёт для ряда значений :

(1.46)

можно построить магнитную характеристику (кривую намагничивания) машины (рис. 1.15).

Рис. 1.15. Магнитная характеристика:

(1) – кривая намагничивания машины;

(2) – ненасыщенная характеристика

Если провести касательную к основной кривой намагничивания, то получим ненасыщенную характеристику, и можно определить коэффициент насыщения:

. (1.47)

Здесь АВ = F_δ – МДС, расходуемая на создание и проведение потока через воздушный зазор;

– сумма МДС, расходуемая на создание и проведение потока через ферромагнитные участки магнитопровода.

Проектировать машину с ненасыщенной магнитной цепью невыгодно, т.к. материалы будут недоиспользованы, но нецелесообразно и проектировать машину с очень насыщенной магнитной цепью, т.к. в этом случае МДС возбуждения велика и необходимо выполнить мощную обмотку возбуждения с большим расходом меди и с большими потерями на возбуждение. Таким образом, рабочая точка должна лежать на перегибе магнитной характеристики.

Якорные обмотки машины постоянного тока

Общие замечания

Обмотка якоря является важным элементом ЭМПТ и должна удовлетворять следующим требованиям:

1. Обмотка якоря должна быть рассчитана на заданные величины напряжения, тока нагрузки, соответствующие номинальной мощности;

2. Обмотка якоря должна обладать достаточной электрической, механической, термической прочностью;

3. Обмотка якоря должна быть экономичной по расходу обмоточного материала (медь, алюминий) и изоляционного материала;

4. Обмотка якоря должна быть технологичной, т.е. технология изготовления должна быть простой, и недорогой).

Обмотки якоря бывают следующих типов:

1) петлевые (простые, сложные);

2) волновые (простые, сложные);

Якорные обмотки выполняются преимущественно из медного провода круглого или прямоугольного сечения, и укладываются в пазы на внешней поверхности якоря. Обмотка якоря выполняется из секций (катушек).

Секции могут выполняться

· Одно – (число витков в секции W_с=1);

Секция состоит из одного или нескольких последовательно соединённых витков, и присоединена своими концами к коллекторным пластинам. В обмотке все секции имеют одинаковое число витков. На схемах обмоток для простоты секции изображаются одновитковые.

Обмотка якоря выполняется двухслойная, т.е. по высоте паза укладывается в 2 слоя, с изоляцией между слоями (рис. 1.17). По ширине паза может выполняться от 1 до 5 катушечных сторон (рис. 1.17).

Паз с – элементарный; – реальный паз. Число элементарных пазов можно определить как:

, (1.48)

где z – число реальных пазов (зубцов).

Если обмотка выполняется из N проводников, то число секций обмотки якоря:

. (1.49)

Так как каждая секция имеет 2 конца, и к каждой коллекторной пластине присоединены 2 конца секций, то общее число пластин коллектора:

(1.50)

Схема обмотки якоря выполняется по шагам.

Шаги обмотки якоря (рис. 1.18):

1. – первый частичный шаг (ширина секции);

2. – второй частичный шаг (расстояние между концом первой секции и началом следующей по схеме);

3. – результирующий шаг (расстояние между началами секций);

4. – шаг по коллектору (расстояние между коллекторными пластинами, к которым присоединены начало и конец одной секции).

Обмотка якоря может быть выполнена:

1) с полным (диаметральным) шагом: ;

2) с укороченным шагом: ;

3) с удлинённым шагом: ,

где – полюсное деление.

Простая петлевая обмотка.

Выполним развёрнутую схему простой петлевой обмотки со следующими данными:

К = S = z_э = 12; 2p =4; ; ; .

Предварительно выполним схему соединений секционных сторон, по шагам (рис. 1.19).

Рис. 1.19. Схема соединений секционных сторон

По данной схеме выполним развёрнутую схему простой петлевой обмотки, которая представлена на рис. 1.20.

Рис. 1.20. Развернутая схема простой петлевой обмотки

Щётки устанавливаются на тех коллекторных пластинах, к которым присоединены секционные стороны, лежащие вблизи геометрической нейтрали. Так как при вращении якоря некоторая часть секций оказывается замкнутой накоротко через щётки и коммутируют, и чтобы индуктируемые в данных секциях ЭДС были минимальными, и не было больших бросков тока, такие секции должны находиться на линии геометрической нейтрали.

Число щёток – ; в данном случае ; ширина щётки – в_щ>в_к.п. где в_к.п. – ширина коллекторной пластины.

Мысленно совершим обход цепи обмотки слева направо (проходим против направления е_а) от первой щётки проходим, секции 1, 2, 3 и приходим к щётке 2. Эти 3 секции составляют одну параллельную ветвь, ЭДС которой равна сумме ЭДС этих секций.

Затем от второй щётки через секции 4, 5, 6 движемся по направлению е_а, секция 6, оказывается, замкнута накоротко через щётки и коммутирует.

Таким образом, простая петлевая обмотка имеет 2а = 2р параллельных ветвей, в данном случае, . В каждой ветви в данном случае 3 секции.

Чтобы обмотка работала нормально, каждая параллельная ветвь должна состоять из одинакового числа секций, и ЭДС всех параллельных ветвей должны быть равны, все секции должны быть одинаково загружены током, и все параллельные ветви должны находиться в одинаковых магнитных условиях, т.е. потоки полюсов должны быть равны. В противном случае в якорной обмотке возникают уравнительные токи, нарушающие работу обмотки якоря и ЭМ в целом.

Обмотка, в которой выполняются все указанные условия, называется симметричной.

Итак, условия симметрии обмотки якоря ЭМПТ:

1. – целое число, т.е. каждая параллельная ветвь должна состоять из одинакового числа секций;

2. – целое число;

3. – целое число, т.е. каждая параллельная ветвь должна находиться в одинаковых магнитных условиях.

Здесь – число секций; – число зубцов (пазов).

Уравнительные соединения

Характерные признаки простых петлевых обмоток:

1. .

2. .

3. Применяются уравнители I рода.

В простой петлевой обмотке, если не выполняются условия симметрии обмотки якоря, и даже если выполняются все условия симметрии, могут возникать уравнительные токи.

Причиной их возникновения в последнем случае может быть магнитная несимметрия ЭМ, которая может быть вызвана различными факторами производственного и технологического характера, в частности:

· Неоднородность материала сердечника;

· Наличие воздушных раковин в литой станине;

Покажем, что происходит в случае прогиба вала (рис. 1.21).

В результате прогиба вала зазор под нижними полюсами уменьшился по сравнению с воздушным зазором под верхними полюсами , следовательно, поток нижней пары полюсов увеличивается по сравнению с потоком, созданным верхней парой полюсов:

, (1.51)

где – магнитное сопротивление потоку нижней и верхней пары полюсов; – МДС возбуждения.

Следовательно, ЭДС, индуцируемая в нижних секциях обмотки якоря больше, чем ЭДС, индуцируемая в верхних секциях обмотки якоря, т.к. е

dФ. Разница ЭДС нижних и верхних секций вызывает уравнительный ток, протекающий по обмотке якоря от нижних секций к верхним.

Уже при холостом ходе в обмотке якоря будут циркулировать уравнительные токи, которые замыкаются через щётки одинаковой полярности с соединительные провода между ними, а так как внутреннее сопротивление обмотки якоря мало, то уравнительные токи могут быть значительными уже при небольшой разности потоков полюсов.

При работе машины уравнительный ток достигает

. (1.52)

При работе машины уравнительные токи складываются с токами нагрузки, в результате чего пара щёток перегружается, возникает искрение, и правильная работа щёточного контакта нарушается.

Чтобы не пропустить уравнительные токи через щётки во внешнюю цепь и дать им возможность замыкаться внутри машины, ставят уравнительные соединения, или уравнители I рода. Это медные проводники малого сопротивления, соединяющие точки обмотки якоря теоретически равного потенциала.

Уравнительный ток, замыкающийся по обмотке якоря и по уравнителю, создаёт магнитный поток, который стремится сгладить магнитную несимметрию, т.е. в данном случае будет ослаблять поток нижней пары полюсов, и усиливать поток верхней пары полюсов.

Сечение уравнителя выбирается равным:

, (1.53)

где – сечение обмотки якоря.

Обычно устанавливается полное число уравнителей I рода:

, (1.54)

где , – число коллекторных пластин и пар полюсов соответственно.

Уравнители устанавливаются с шагом:

. (1.55)

Этот шаг называют ещё потенциальным шагом , т.к. он равен расстоянию между точками теоретически равного потенциала обмотки якоря.

Уравнители I рода могут выполняться:

· На стороне коллектора, т.е. соединяют коллекторные пластины теоретически равного потенциала;

· Или на противоположной от коллектора стороне, т.е. соединяют равнопотенциальные точки лобовых частей обмотки якоря.

Простые волновые обмотки

Характерные признаки простых волновых обмоток:

1. ;

2. ;

3. не требуется применение уравнителей I рода.

Принцип выполнения простой волновой обмотки рассмотрим на примере ЭМПТ, (рис. 1.22).

При одном обходе якоря (рис. 1.22) сделано р – шагов по коллектору (в данном случае – 4 шага), и оказались пройденными все коллекторные пластины, кроме одной (справа или слева от начальной), тогда

(1.56)

Тогда шаг обмотки, равный шагу по коллектору:

– целое число, (1.57)

при этом знак «–» соответствует неперекрещивающейся обмотке;

Простая волновая обмотка называется последовательной, т.к. она независимо от числа пар полюсов образует 2 параллельные ветви (рис. 1.23):

(1.58)

Необходимое число щёток простой волновой обмотки:

(1.59)

Поскольку каждая из ветвей простой волновой обмотки проходит под всеми полюсами, то неравенство потоков полюсов (магнитная несимметрия, вызванная различными факторами) не вызывает неравенства ЭДС, и не появляются уравнительные токи, и поэтому не требуется применение уравнителей I рода.

1.5.5. Развёрнутая схема простой волновой обмотки (пример)

Выполним развёрнутую схему простой волновой обмотки со следующими данными:

;

.

Рассчитаем шаги обмотки:

, где – число, дополняющее отношение до целого числа;

.

Предварительно выполним схему соединений секционных сторон, по шагам (рис. 1.24).

По данной схеме выполним развёрнутую схему простой петлевой обмотки, которая представлена на рис. 1.25.

Рис. 1.25. Развернутая схема простой волновой обмотки

На рис. 1.25 выделены две начальные секции.

Установлено полное число щёток:

. (1.60)

Данная обмотка имеет 2 параллельные ветви, каждая состоит из 5 секций.

Сложные обмотки

Сложная петлевая обмотка

Сложная петлевая обмотка – это обмотка, состоящая из m простых петлевых обмоток, расположенных на одном якоре и соединённых параллельно с помощью щёток. Здесь m – число ходов обмотки.

Выполняются обмотки с:

– двухходовая обмотка

– трехходовая обмотка (1.61)

Характерные признаки сложной петлевой обмотки:

1. ;

2. ;

3. применяются уравнители I, II рода.

Для обеспечения равномерного распределения токов между простыми обмотками, входящими в состав сложной, применяются уравнители II рода. Уравнители II рода соединяют точки теоретически равного потенциала простых обмоток, входящих в состав сложных. Применение уравнителей II рода, при , показано на рис. 1.26.

Рис. 1.26. Уравнители II рода

В сложных обмотках ширина щётки:

, (1.62)

где – ширина коллекторной пластины.

Сложные петлевые обмотки могут быть двукратнозамкнутые и однократнозамкнутые (рис. 1.27). Однократнозамкнутые обмотки– в том случае, если K – нечётное, и тогда последняя секция одной обмотки соединяется с начальной секцией второй обмотки. В двукратнозамкнутых обмотках на якоре располагается 2 независимые обмотки, которые соединяются только щётками.

Сложная волновая обмотка

Сложная волновая обмотка – это обмотка, состоящая из m простых волновых обмоток, расположенных на одном якоре и соединённых параллельно с помощью щёток.

Выполняются обмотки с:

– двухходовая обмотка

– трехходовая обмотка (1.63)

Характерные признаки сложной волновой обмотки:

1. ;

2. ;

3. применяются уравнители II рода.

Комбинированные («лягушачьи») обмотки

Комбинированные обмотки представляют собой совокупность простой петлевой и сложной волновой обмоток, которые расположены в общих пазах, присоединены к общему коллектору и работают параллельно. Так как каждая из обмоток двухслойная, то в пазу располагается 4 обмоточных слоя. Каждая из обмоток рассчитывается на , и ЭДС двух обмоток равны. Каждая из обмоток рассчитывается на половину мощности машины.

Секции сложной волновой обмотки играют роль уравнителей I рода для простой петлевой обмотки, а секции простой петлевой обмотки играют роль уравнителей II рода для сложной волновой обмотки. Поэтому не требуется применять никакие уравнительные соединения.

При выборе типа обмотки якоря определяющим является ток параллельной ветви обмотки, который для ЭМПТ средней мощности:

. (1.64)

Источник