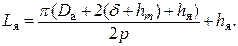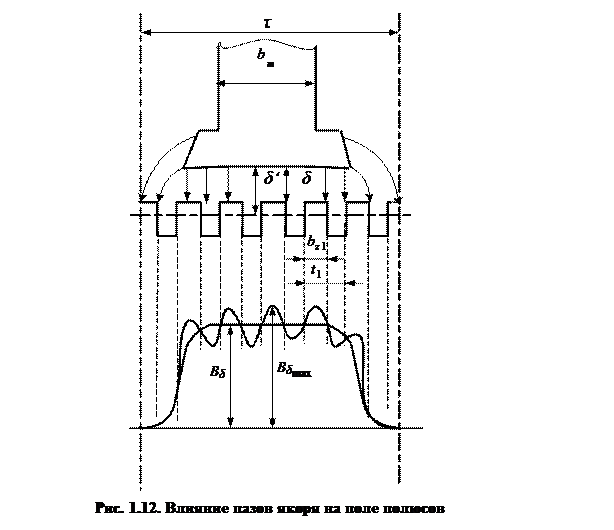Магнитная цепь электрической машины
§19. Магнитная цепь
Для того чтобы сосредоточить магнитное поле в определенной части электрической машины, аппарата или прибора и уменьшить мощность, потребляемую катушкой электромагнита, создающего это поле, в конструкции этих устройств широко применяют различные элементы из ферромагнитных материалов. Совокупность таких элементов с разделяющими их воздушными зазорами составляет магнитопровод, или магнитную цепь, электрической машины, аппарата или прибора. Например, магнитная цепь электромагнитного реле (рис. 46, а) состоит из трех участков: сердечника 2, якоря 4 и двух воздушных зазоров 6. По замкнутому контуру, образованному этими участками, проходит магнитный поток 3, создаваемый током катушки 1. При переходе через воздушные зазоры, разделяющие сердечник и якорь, часть магнитного потока замыкается по воздуху, т. е. не проходит через якорь,— возникает поток рассеяния 5.
Магнитное поле в магнитной цепи электрической машины постоянного тока создается током катушек 7 (рис. 46, б), расположенных на полюсах 8. Эти катушки называют обмотками возбуждения. Создаваемый ими магнитный поток проходит через сердечники полюсов, вращающуюся часть машины — якорь 9, воздушные зазоры 11 между полюсами и якорем и замыкается через остов 10.
Магнитодвижущая сила. Способность тока возбуждать магнитное поле оценивается его магнитодвижущей силой (м. д. с). Магнитодвижущая сила F изменяется в амперах. Магнитодвижущая сила проводника с током I равна силе этого тока: F = I.
В общем случае, когда какой-либо замкнутый контур охватывает несколько токов (показан на рис. 47, а штриховой линией), суммарная магнитодвижущая сила равна их алгебраической сумме:
Для случая, показанного на рис. 47, а,


F = I? (45′)
Закон Ома для магнитной цепи. Для лучшего понимания условий возникновения магнитного поля в магнитных цепях целесообразно провести аналогию между магнитной цепью и цепью электрической. Это можно сделать, например, для простейшей магнитной цепи, на всем протяжении которой напряженность Н магнитного поля постоянна. Для такой цепи произведение напряженности Н на длину l магнитной цепи по всему ее замкнутому контуру равно алгебраической сумме токов, охватываемых этим контуром:
Ф = F/R м (47)
Из формулы (47) следует, что действие магнитодвижущей cилы аналогично действию электродвижущей силы. Подобно тому как э. д. с. является причиной возникновения тока в электрической цепи, так и м. д. с. является причиной возникновения магнитного потока в магнитной цепи. Чем больше магнитодвижущая сила F, создаваемая катушкой электромагнита, тем больший магнитный поток проходит по его магнитной цепи.
Магнитная и электрическая цепи машин постоянного тока
Магнитная цепь машины предназначена для создания и распределения магнитного поля в воздушном зазоре и состоит из главных полюсов, сердечника якоря, воздушного зазора между полюсами и якорем и ярма (станины). В зависимости от числа главных полюсов магнитная система может быть двух- (рис. 1.1), четырех-(рис. 1.6), шестиполюсной и т.д. Пути магнитного потока для четырехполюсной машины показаны на рис. 1.6.
Распределение магнитной индукции в рабочем воздушном зазоре характеризуется кривой В (α) (рис. 1.7), где α – дуга окружности якоря (на рис. 1.7 магнитная система развернута в плоскость). Почти постоянное значение индукции В в воздушном зазоре необходимо для получения примерно постоянной ЭДС в проводниках, находящихся под полюсом, и оно обеспечивается специальной формой полюсных наконечников.
Линии симметрии m, n, делящие пространство между полюсами пополам, называются геометрическими нейтральными линиями, а линии, проходящие через точки, где В = 0, — физическими нейтральными линиями (в данном случае геометрическая и физическая нейтральные линии совпадают). Дуга между соседними нейтральными линиями называется полюсным делением. Она обозначается буквой τ и может выражаться в метрах, градусах, радианах, числе пазов и в других удобных для расчета единицах.
Электрическая цепь машины состоит из обмотки якоря, коллектора и щеток. Как указывалось, проводники якоря, соединяясь через коллекторные пластины, образуют замкнутую цепь. При вращении якоря по часовой стрелке проводники обмотки якоря пересекают магнитное поле полюсов и в них наводится переменная ЭДС: в верхней половине обмотки ЭДС направлены от нас, в нижней – к нам.

В обмотке якоря относительно внешней цепи образуются две параллельные ветви, ЭДС которых равны и которые во внешней цепи действуют согласно. При вращении якоря картина распределения ЭДС не изменяется, меняются только номера проводников, входящих в параллельные ветви. Разность потенциалов между щетками остается практически постоянной (если пренебречь небольшими пульсациямии ЭДС).
Замкнутую обмотку якоря можно получить двумя способами: соединять на коллекторе проводники обмотки двигаясь вперед – назад, т.е. возвращаясь назад к соседнему проводнику (рис. 1.9, а), или только вперед, обходя проводники якоря, двигаясь все время в одном направлении (рис. 1.9,б). Очевидно, что в любом случае каждый следующий проводник должен находится под полюсом противоположной полярности.
Это означает, что шаг обмотки близок к полюсному делению τ. В первом случае получаем так называемую петлевую обмотку, во втором – волновую обмотку.
В петлевых обмотках при числе полюсов больше двух (6, 8 и т.д.) число параллельных ветвей и щеток равно числу полюсов. В волновых обмотках число параллельных ветвей и щеток вне зависимости от числа полюсов равно двум.
Магнитная цепь машины постоянного тока
Если по катушкам машины постоянного тока, расположенным на главных полюсах, начнет протекать ток, вокруг катушек полюсов будет создаваться магнитное поле.
В зависимости от направления тока в обмотке возбуждения, полюса будут иметь разную полярность.
Для того чтобы машина постоянного тока могла работать, число полюсов всегда должно быть парным.
Магнитное поле обозначается магнитными силовыми линиями. Направление всегда от северного полюса к южному.
Магнитные силовые линии в машине постоянного тока должны быть замкнуты между полюсами противоположной полярности.
При расчете магнитной цепи принято использовать среднюю магнитную силовую линию. Прежде чем нарисовать эту линию, введем понятие средней линии полюсов.
Средняя линия полюсов — это плоскость, проходящая вдоль машины через центр посередине полюсов. Средняя магнитная силовая линия обозначает основной магнитный поток, который обозначается Фδ.
Основным магнитным потоком называется поток, создаваемый полюсом и через воздушный зазор сцепляющийся с обмоткой якоря. Число основных магнитных потоков равно числу полюсов.
Eа — ЭДС обмотки якоря.
Cм — машинная постоянная. Она зависит от конструкции якоря машины и для каждой конкретной машины — величина постоянная.
Фδ — основной магнитный поток.
ω — угловая скорость вращения.
M — момент, развиваемый двигателем на валу.
Iа — ток якоря.
Pэм — электромагнитная мощность. Служит доказательством того, что от магнитного потока зависит мощность машин.
Кроме основного магнитного потока вокруг полюсов создаются магнитные потоки, которые не соединяются с якорем, они называются потоками рассеяния и обозначаются Фσ. Потоки рассеяния возникают в местах крепления железа полюса к корпусу и на концах башмаков.
Основной задачей расчета магнитной цепи является определение числа витков и тока одного витка, необходимых для создания магнитного потока и проведения его через магнитную цепь машины.
Произведение числа витков на ток называется намагничивающей силой цепи. Величина намагничивающей силы цепи зависит от сопротивления цепи прохождению магнитного потока.
Для того чтобы определить сопротивление магнитной цепи, ее делят на участки, исходя из условия, что магнитное сопротивление, выражаемое в напряженности по всей длине участка, будет постоянным. Таких условий пять:
1. Воздушный зазор и его магнитное сопротивление.
Fδ=Hδ·δ
Hδ — напряженность воздушного зазора.
2. Зубцы якоря.
Fz=Hz·hz
Fz — магнитное сопротивление зубца;
Hz — напряженность в зубце;
hz — высота зубца.
3. Ярмо якоря.
Fа=Hа·Lа
Fа — магнитное сопротивление ярма;
Hа — напряженность в ярме;
Lа — длина магнитной силовой линии.
4. Полюса.
Fm=Hm·hm
hm — длина магнитной силовой линии (высота статора).
5. Магнитное сопротивление ярма статора.
Fя=Hя·Lя
Lя — длина магнитной силовой линии в ярме статора.
Намагничивающая сила цепи должна быть равна сумме магнитных сопротивлений участков цепи.
Воздушный зазор в машине постоянного тока колеблется от 2 до 4 мм и, несмотря на такую маленькую величину, воздушный зазор оказывает самое большое сопротивление прохождению магнитного потока.
От точности расчета воздушного зазора зависит точность определения намагничивающей силы цепи, а соответственно мощности и габаритов машины.
Магнитная цепь машины постоянного тока
Магнитопровод – деталь электрических машин, предназначенная для усиления потока магнитной индукции на определенных участках магнитного поля. Магнитопровод машин и аппаратов с переменным или пульсирующим магнитным полем изготавливается из тонких изолированных стальных листов для уменьшения потерь из-за токов Фуко.
Магнитная цепь – это путь, по которому замыкаются магнитные силовые линии основного магнитного потока.
Основной магнитный поток Фδ – это поток в зазоре δ, приходящийся на один главный полюс машины и проходящий из статора в ротор. Величинаосновного магнитного потока определяет величину индуктируемой в обмотке якоря ЭДС. Магнитная цепь ЭМПТ симметрична. Рассмотрим её на пару полюсов. Магнитная цепь машины постоянного тока приведена на рисунке 1.10.
Рис. 1.10. Магнитная цепь ЭМПТ:
ha – высота спинки якоря;
hz – высота зубца ( паза) якоря;
δ – воздушный зазор;
Dа – наружный диаметр ротора;
Фδ – основной магнитный поток;
iв – ток обмотки возбуждения;
Часть потока, создаваемого полюсами, не проникает из статора в ротор через зазор, а рассеивается непосредственно вокруг обмотки возбуждения, называется потоком рассеяния – Фσ.
Тогда полный поток, созданный полюсами, будет:
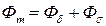

где кσ – коэффициент рассеяния полюса:
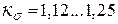
1.4.1. Расчёт магнитной цепи ЭМПТ
Магнитная цепь ЭМПТ рассчитывается в режиме холостого хода, т.е. ток якоря Ia = 0.
В основе расчёта лежит закон полного тока:
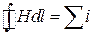
где Н – напряжённость магнитного поля;
dl – элемент длины магнитной силовой линии;
∑i – полный ток, охватываемый магнитной линией.
При расчёте магнитную цепь ЭМПТ разбивают на пять участков. Каждый участок по всей своей длине имеет одинаковое сечение, одинаковое значение магнитной индукции и одинаковую магнитную проницаемость, т.е. на всём протяжении участка напряжённость магнитного поля (Н = const):
1) воздушный зазор – δ;
Тогда по (1.11) запишем:
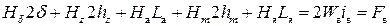
Здесь Fв – МДС возбуждения.
Поверочный расчёт магнитной цепи заключается в определении МДС возбуждения по заданным номинальным данным машины (Рн, nн, Uн, ηн, Iaн).
1. Приведём расчёт МДС магнитного зазора.
Рассмотрим ЭМПТ в пределах полюсного деления τ (рис. 1.11). При этом предположим, что якорь гладкий, т.е. пазы и зубцы отсутствуют.
Тогда магнитная индукция на протяжении полюсного деления распределяется по трапецеидальному закону (рис. 1.11, а), и индукция по длине машины распределяется также по трапецеидальному закону, максимальна и одинакова под полюсом, и поле ослабляется до нуля к торцам якоря (рис. 1.11, б).
На рис. 1.11, lа, lm – длины сердечников якоря и полюса соответственно. Тогда расчётная длина якоря lб находится при замене трапецеидальной кривой магнитного поля по длине машины (рис. 1.11,б) равновеликим по площади прямоугольником с основанием lб и высотой Вб:
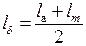
Расчётная длина полюсной дуги bб находится при замене трапецеидальной
кривой магнитного поля в пределах полюсного деления (рис. 1.11,а) равновеликим по площади прямоугольником с основанием bб и высотой Вб:

где αδ – коэффициент полюсной дуги, αδ = 0,6…0,85
Тогда определим магнитную индукцию в зазоре:

После расчёта номинальной магнитной индукции в зазоре, необходимо сверить полученной значение с рекомендуемыми:

Затем рассчитывается напряжённость магнитного поля в воздушном зазоре:

где 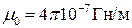
Тогда МДС воздушного зазора на пару полюсов при гладком якоре:

Но при наличии на якоре пазов, поле под ними ослабляется, и кривая поля в этом случае приобретает зубчатый вид (рис. 1.12).
Наличие пазов приводит к увеличению воздушного зазора, при этом вводят понятие эквивалентного воздушного зазора, который определяется как:
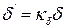
Здесь 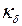
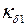
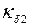
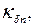
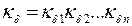
Пусть 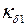
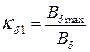
Коэффициент 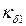

где t1 – зубцовое деление; 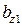
Найденное значение 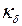

Тогда МДС воздушного зазора при учёте неравномерности зазора на пару полюсов:

2. Приведём расчёт МДС пазово-зубцовой зоны.
Расчёт пазово-зубцовой зоны производят на одно пазовое деление 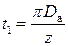
Возьмём произвольное сечение на расстоянии х от низа паза (рис. 1.13). Тогда магнитный поток, приходящийся на одно пазовое деление:

Этот поток делится на поток, проходящий через зубец, и поток, проходящий через паз:
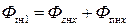
Разделим обе части последнего выражения на сечение зубца (на расстоянии х от низа паза):

а второе слагаемое правой части помножим и разделим на сечение паза (на расстоянии х от основания паза):
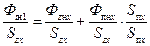

где 
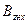


Тогда в сечениях 1,3, и среднем сечении, магнитная индукция будет:

При расчёте 
Здесь 

где nк, bк – число и ширина вентиляционных радиальных каналов (рис. 1.14).
Если магнитная индукция в данном сечении зубца, например, в сечении х, 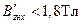

Затем по основной кривой намагничивания 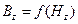

Если магнитная индукция в данном сечении зубца 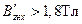

и напряжённость поля в данном сечении 

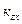
Таким образом, определили напряжённость поля в 3-х сечениях зубца 
По формуле Симпсона определим усреднённое значение 
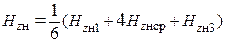
Тогда МДС зубцовой зоны на пару полюсов:

3. Приведём расчёт МДС спинки якоря.
Определим магнитную индукцию в спинке якоря:

Затем по основной кривой намагничивания 
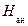
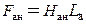
Здесь 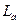
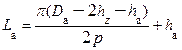
4. Приведём расчёт МДС полюса.
Определим магнитную индукцию в сердечнике полюса:
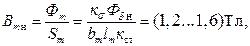
где кσ – коэффициент рассеяния полюса, 
Затем по кривой намагничивания 


5. Приведём расчёт МДС ярма.
Определим магнитную индукцию в ярме:

Затем по основной кривой намагничивания 

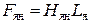
Здесь