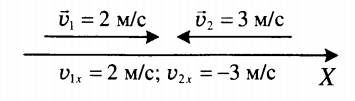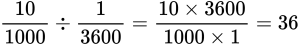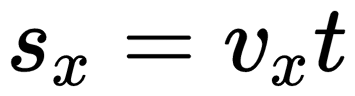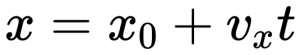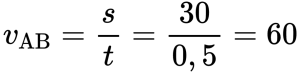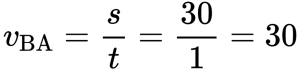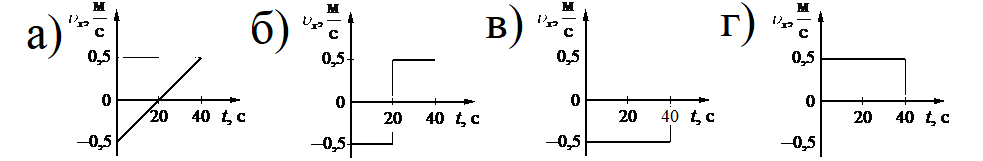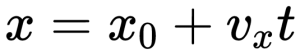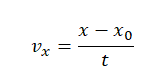Возможно ли равномерное прямолинейное движение автомобиля при работающем двигателе

Друзья! Помогите мне указать и сравнить силы, действующие на автомобиль. № 130. ГДЗ Физика 10 класс Рымкевич.

Указать и сравнить силы, действующие на автомобиль,
когда он: а) стоит неподвижно на горизонтальном участке доро-
ги; б) трогается с места; в) движется равномерно и прямолиней-
но по горизонтальному участку; г) двигаясь равномерно, прохо-
дит середину выпуклого моста; д) двигаясь равномерно, повора-
чивает; е) тормозит на горизонтальной дороге.

а) Сила тяжести направлена вертикально
вниз, сила реакции опоры вертикально вверх. Эти си-
лы равны по модулю и компенсируют друг друга.

б) В вертикальном направлении действуют те же си-
лы, что и в случае а). В горизонтальном направлении
на автомобиль действует сила трения покоя, обеспе-
чивающая ускорение автомобиля в этом направле-
нии.

в) К силам, перечисленным в пунктах а) и б), добавля-
ется сила трения качения и сила сопротивления возду-
ха. Эти силы действуют в направлении, противопо-
ложном движению автомобиля. В случае равномерно-
го прямолинейного движения эти силы компенсируют
силу трения покоя колес с поверхностью дороги.

г) Нормальная компонента силы реакции опоры
меньше силы тяжести. Ненулевая векторная сумма
этих двух сил направлена вниз и обеспечивает цент-
ростремительное ускорение, возникающее при дви-
жении по выпуклому мосту.

д) Сила трения покоя колес о поверхность дороги име-
ет компоненту, направленную к центру маленькой
окружности, по дуге которой поворачивает автомо-
биль.

е) Действуют те же силы, что и в случае в), но сила
трения покоя направлена в ту же сторону, что и силы
трения качения и сопротивления воздуха. Равнодей-
ствующая этих сил и обеспечивает замедленное дви-
жение автомобиля.

Источник

Может ли автомобиль двигаться равномерно по горизонтальному шоссе с выключенным двигателем?

Ответ или решение 3

Понятие равномерного движения

Под равномерным движением понимают движение, при котором наблюдаемый объект движется с постоянной скоростью. Различают равномерное прямолинейное движение и равномерное движение по окружности (при котором скорость тела неизменна по модулю, но изменяется по направлению).

Условием равномерного прямолинейного движения является равенство нулю суммы действующих на тело сил.

Действующие на автомобиль силы

Рассмотрим силы, действующие на автомобиль, движущийся по шоссе. Это будут:

Поскольку автомобиль движется по горизонтальному шоссе, сила тяжести направлена по нормали к вектору его скорости и не может повлиять на нее. Казалось бы, автомобиль с выключенным двигателем может двигаться равномерно. Однако на автомобиль действуют силы трения со стороны набегающего воздуха, потери на внутреннее трение в механизмах и сопротивление качению, связанная с деформацией покрышек при контакте с дорожным покрытием. Все перечисленные факторы работают на замедление автомобиля, таким образом, появляется отрицательное ускорение и автомобиль с выключенным двигателем не перемещается равномерно, а замедляется.

При выключенном двигателе автомобиль не может двигаться равномерно прямолинейно согласно 1 закона Ньютона.

1 закон Ньютона гласит, что тело может находится в состоянии равномерного прямолинейного движения или покоя, если на него не действуют силы или действия всех сил скомпенсированы.

На автомобиль, с выключенным двигателем, действует только одна сила трения колес о поверхность дороги. Автомобиль будет двигаться с ускорением.

Источник

Равномерное прямолинейное движение

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ​ \( t \) ​ тело совершило перемещение ​ \( \vec \) ​, то скорость его движения ​ \( \vec \) ​ равна ​ \( \vec=\frac<\vec>\) ​.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

4. Зависимость координаты от времени можно представить графически.

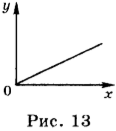
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ​ \( x \) ​ = 4 м/с · ​ \( t \) ​. Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них ​ \( t \) ​ = 0 и ​ \( x \) ​ = 0, а другая ​ \( t \) ​ = 1 с, ​ \( x \) ​ = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

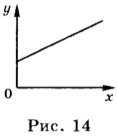
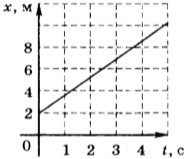
Если в начальный момент времени координата тела ​ \( x_0 \) ​ = 2 м, а проекция его скорости ​ \( v_x \) ​ = 4 м/с, то уравнение движения имеет вид: ​ \( x \) ​ = 2 м + 4 м/с · ​ \( t \) ​. Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ​ \( t \) ​ = 0, ​ \( x \) ​ = 2 м (рис. 14).

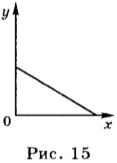
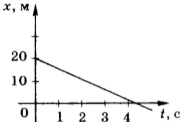
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) ​ = 2 м – 4 м/с · ​ \( t \) ​. График зависимости координаты такого движения от времени представлен на рисунке 15.

Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

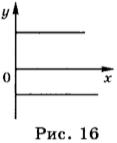
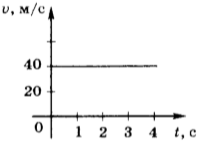
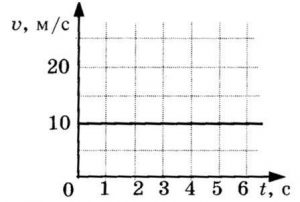
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

Применим эту последовательность действий к приведённой выше задаче.

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

Система отсчёта связана с Землёй, ось ​ \( Ox \) ​ направлена в сторону движения первого тела, начало отсчёта координаты — т. ​ \( O \) ​ — положение первого тела в начальный момент времени.

Начальные условия: ​ \( t \) ​ = 0; ​ \( x_ <01>\) ​ = 0; \( x_ <02>\) = 270.

Уравнения для каждого тела с учётом начальных условий: ​ \( x_1=v_1t \) ​; ​ \( x_2=l-v_2t \) ​. В месте встречи тел ​ \( x_1=x_2 \) ; следовательно: ​ \( v_1t=l-v_2t \) ​. Откуда ​ \( t=\frac\cdot t \) ​. Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ​ \( x \) ​ = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

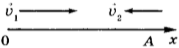
1) ​ \( v_1=v_2 \) ​
2) ​ \( v_1=2v_2 \) ​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

1) ​ \( v_1=v_2 \) ​
2) ​ \( v_1=2v_2 \) ​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

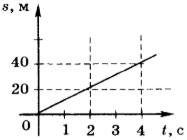
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

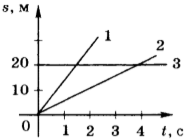
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​ \( v_1 \) ​, \( v_2 \) и \( v_3 \) движения этих тел.

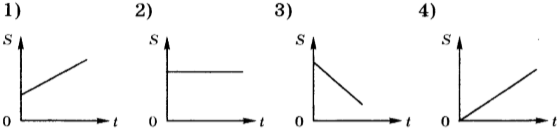
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​ \( x=1t \) ​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

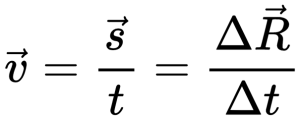
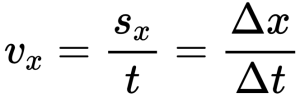
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

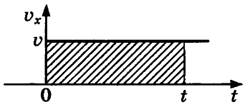
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

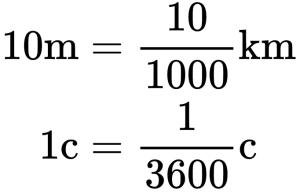
Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

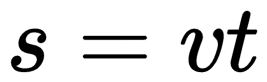
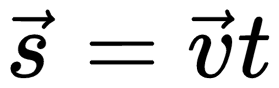
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

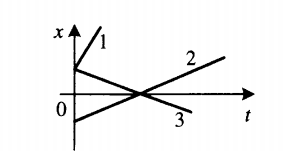
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

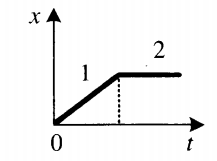
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

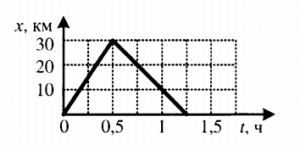
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

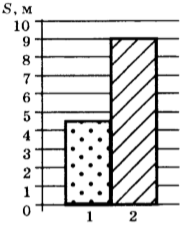
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Прямолинейное равномерное движение

Содержание:

Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Прямолинейное равномерное движение

Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения. Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Механическое движение

Вдали на дороге виден автомобиль. Мы не слышим шума его мотора и не видим, вращаются его колёса или нет. Как определить—движется автомобиль по дороге или нет?

Проследим за положением автомобиля относительно каких-либо неподвижных предметов, находящихся у дороги, например телеграфных столбов или деревьев. Если расстояние автомобиля от этих неподвижных предметов меняется, мы заключаем, что автомобиль движется; если же не меняется, значит автомобиль находится в покое.

Подобным же образом мы определяем, движется или нет поезд, пароход, самолёт—вообще любое тело.

Изменение положения данного тела относительно других тел называется механическим движением.

Механические движения тел весьма разнообразны. Движение планет, облаков, воды в реках и океанах, поездов, самолётов, автомобилей, различных частей машин и станков, людей, животных, полёт птиц—всё это лишь немногие примеры механических движений.

Все тела природы, все частицы, из которых состоят эти тела, находятся в движении. На первый взгляд кажется, что это не всегда верно; например, дома стоят неподвижно, неподвижны горы, леса и многие другие предметы. В действительности же все эти предметы неподвижны только относительно друг друга, но они вместе с Землёй совершают суточное вращение и движутся вокруг Солнца.

В природе не существует совершенно неподвижного тела.

Механическое движение совершают все тела природы и частицы, из которых состоят эти тела.

Механические движения изучаются в разделе физики, называемом механикой. Слово механика произошло от греческого слова „механэ“, что значит машина или приспособление.

Машины ещё в глубокой древности применялись в транспорте, а также в строительном и военном деле. На рисунке 2 изображено применение древними египтянами рычагов при постройке пирамид.

Рис. 2. Применение рычагов при постройке пирамид в древнем Египте.

Законы механики лежат в основе устройства и сложнейших современных машин. На рисунке 3 изображён современный башенный подъёмный кран, применяющийся на наших стройках. Один такой кран выполняет работу тысячи рабочих.

Относительность движения и покоя

Движением, как мы видели, называется изменение положения данного тела относительно каких-либо других тел. Пароход, например, движется относительно берега, поезд—относительно полотна железной дороги, резец токарного станка—относительно основания станка и т. д. Но и берег, и полотно железной дороги, и основание станка сами находятся в движении вместе с Землёй; мы лишь условно принимаем их за неподвижные тела.

Движение тела относительно других тел, условно принимаемых за неподвижные, называется относительным движением.

Так как все тела природы находятся в движении и абсолютно (Абсолют—от латинского слова абсолютус—безусловный) неподвижных тел нет, то не существует и абсолютных движений, точно так же как не существует и абсолютного покоя.

Всякое движение, так же как и всякий покой, является относительным.

Одно и то же движение, рассматриваемое относительно разных тел, будет представляться по-разному. Представим себе пассажира, сидящего в вагоне движущегося поезда. Что можно сказать о его движении? Проводник вагона скажет о пассажире, что он неподвижен (сидит), стрелочник, мимо которого движется поезд, уверяет, что пассажир движется мимо него. И в сущности каждый из них прав. Проводник вагона, заявляя о том, что пассажир не движется, рассматривает положение пассажира относительно предметов в вагоне. Стрелочник, стоящий на земле и наблюдающий за движением поезда, рассматривает положение пассажира или относительно полотна дороги, или относительно себя.

Так как два наблюдателя рассматривали положение пассажира относительно разных предметов,то они и пришли к различным выводам.

Рассмотрим другой пример. Пассажир находится в закрытой каюте речного парохода, где он видит только стены каюты и закрытое занавеской окно. Может ли он сказать что-либо определённое о движении парохода? При спокойном ходе парохода, не слыша шума работы машины, невозможно определить, движется пароход или нет. Надо открыть окно, найти какой-либо неподвижный предмет на берегу и только по изменению расстояния от этого предмета можно будет судить о движении парохода.

Рис. 3. Башенный кран, применяющийся на стройках.

Таким образом, желая определить, движется тело или нет
и как оно движется, мы должны указать, относительно каких тел рассматривается интересующее нас движение.

Тела, относительно которых рассматривается движение, называются телами отсчёта.

В дальнейшем при изучении различных движений в качестве тела отсчёта мы будем брать Землю или какое-либо другое тело, неподвижное относительно Земли, например стол физического кабинета, где производятся опыты.

Вопрос об относительности движения и покоя изучался знаменитым итальянским учёным Галилео Галилеем. Ниже приводится выписка из его книги, впервые опубликованной в 1632 г., в которой он излагает свои взгляды по данному вопросу.

Движение твёрдого тела и движение точки

Механические движения тел в природе и технике могут быть весьма разнообразны и сложны.

Наиболее простым видом движения тела является поступательное движение. При поступательном движении любая прямая, проведённая в теле, остаётся параллельной самой себе.

Поступательным движением является, например, движение ящика, выдвигаемого из стола, движение поршня в цилиндре паровой машины или в двигателе внутреннего сгорания, движение вагона на прямолинейном участке железнодорожного пути, движение резца вдоль корпуса токарного станка (рис. 4) или детали на продольно-строгальном станке относительно резца (рис. 5). На рисунке 6 показано поступательное движение карандаша.

Рис. 4. Поступательное движение резца токарного станка.

Рис. 5. Поступательное движение детали на продольно-строгальном станке.

Рис. 6. Поступательное движение карандаша.

В дальнейшем мы часто будем говорить о движении тела, рассматривая его как точку.

Если непрерывно отмечать положение движущегося тела в пространстве точками, например: и т. д. (рис. 7), то получится линия, называемая траекторией движения. Проводя карандашом по бумаге, мы оставляем на ней след—траекторию движения кончика карандаша. Стрельба трассирующими пулями по цели облегчает пристрелку, так как видна траектория движения пули. Попав в атмосферу Земли и раскалившись, метеорит оставляет на короткое время светящийся след, указывающий траекторию его полёта.

Рис. 7. Траектория движущейся точки.

Отсчёт пройденного пути за заданный промежуток времени производится вдоль траектории от некоторой условно выбранной на траектории точки, например от (рис. 7), в которой в момент начала наблюдений находится тело.

Во всяком движении длина пути, пройденного точкой, зависит от времени. Найти способы определять положение точки на траектории в любой момент времени—значит установить закон движения точки.

Закон движения может быть выражен различно: его можно представить в виде математической формулы, связывающей величины, характеризующие движение; можно представить в виде таблицы и, наконец, можно изобразить графически в виде некоторой линии.

Движение точки является определённым, если установлена траектория и известен закон движения её по этой траектории.

Различные виды движения тела

Траектория движения тела может быть прямолинейной и криволинейной. Соответственно этому движения тела разделяются на прямолинейные и криволинейные.

Рис. 9. Примеры криволинейных движений.

На рисунке 9 изображены простейшие примеры криволинейного движения: движение концов стрелок часов и движение мячика, брошенного под углом к горизонту.

Независимо от формы траектории движения разделяются на равномерные и неравномерные.

Равномерным называется такое движение, при котором в любые равные промежутки времени тело проходит одинаковые пути.

Так, например, если тело в первую секунду от начала наблюдения за его движением проходит 10 м, в каждую следующую— также по 10 м, в каждую половину секунды—5 м, в каждую пятую долю секунды—2 ж и т. д., то оно движется равномерно.

Примером равномерного движения, наблюдаемого в природе, может служить движение точки земной поверхности при суточном вращении. За равномерное движение можно принимать движение точек часовой стрелки, движение конвейерной ленты на производстве, движение поезда на длинном и ровном перегоне (равномерность этого движения легко установить, прислушиваясь к стукам при ударе колёс о стыки рельсов) и многие другие.

Рис. 10. Равномерное движение тележки с капельницей.

Установим на тележке капельницу (рис. 10) и при помощи груза уравновесим трение колёс тележки о доску. Затем слегка толкнём тележку. Вытекающие из капельницы капли окрашенной жидкости через равные промежутки времени отметят на бумаге пути, пройденные тележкой. Приблизительно эти пути одинаковы; следовательно, движение тележки с капельницей можно принимать за равномерное движение.

При изучении движения приходится измерять пройденные пути и промежутки времени. Всякие же измерения могут быть произведены только с некоторой степенью точности. Поэтому и равномерность того или иного движения может быть установлена на опыте только с той степенью точности, с которой
производятся измерения.

Скорость движения. Единицы скорости

Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Самолёт, например, движется быстрее автомобиля, а автомобиль может двигаться быстрее самой резвой лошади. Словами „быстро“ и „медленно“ в обыденной речи характеризуют различие в движении тел. В физике величиной, характеризующей различие в быстроте движения тел, является скорость.

В случае равномерного движения о величине скорости мы можем судить по величине пути, который проходит тело за равные промежутки времени. Чем больший путь пройден телом за одно и то же время, тем больше его скорость, и наоборот. Поэтому величина скорости в равномерном движении характеризуется путём, пройденным телом в единицу времени. Следовательно, для нахождения скорости движения надо измерить две величины: путь и время, за которое пройден этот путь. Тогда частное от деления пути на время даст нам величину скорости.

Обозначим скорость буквой v. Если за время t пройден путь s, то скорость:

Скоростью равномерного движения называется величина, измеряемая отношением пути ко времени, за которое этот путь пройден.

Положив в написанной выше формуле s = 1 ед. пути, t = 1 ед. времени, получим ед. скорости.

Это значит, что единицей, скорости является скорость такого движения, при котором за единицу времени тело проходит единицу пути.

Если измерять путь в сантиметрах, а время в секундах, то единицей скорости будет скорость такого движения, при котором тело за 1 сек. проходит 1 см. Наименование такой единицы скорости: Единицами скорости могут быть также: и др.

Положим, что поезд, двигаясь с неизменной скоростью, за 2 часа прошёл путь 72 км. Вычислим скорость движения поезда: s = 72 км; t = 2 часа;

В данном случае единицей скорости является

Найдём численное значение полученной скорости, приняв за единицу скорости

Если же за единицу скорости принять то получим следующее численное значение скорости:

Таким образом, численное значение величины скорости зависит от выбранной нами единицы скорости, или, что то же, от численных значений пути и времени.

При поступательном движении тела все его точки движутся с одной и той же скоростью. Поэтому скорость какой-либо точки тела одновременно будет скоростью всего тела.

Ниже в таблице приведены скорости некоторых движений, наблюдаемых в природе и в современной технике.

Графическое изображение движения

В технике скорость движения определяется с помощью специальных приборов. Один из таких приборов, называемый спидометром, устанавливается на автомобиле (рис. 11). Механизм спидометра соединён с колёсами автомобиля. Скорость движения автомобиля отмечается стрелкой на шкале спидометра.

Рис. 11. Спидометр на автомобиле (справа дан в большем масштабе).

Когда автомобиль движется с переменной скоростью,то стрелка спидометра указывает то на одну, то на другую цифру на шкале; когда же автомобиль движется некоторое время не меняя скорости, стрелка стоит на одном месте шкалы. Спидометр, таким образом, показывает ту скорость, с которой движется автомобиль в каждый данный момент времени.

Чтобы знать о всех изменениях скорости, которые были при движении автомобиля, для этого пришлось бы составить запись скоростей автомобиля в различные моменты времени. Такую запись можно производить автоматически при помощи специального прибора.

Автоматическая запись производится на специально разграфлённой бумаге, которая при помощи часового механизма относительно,пера на ней вычерчивается график движения.
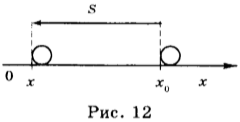
равномерно движется под пишущим пером. Перо с помощью особого приспособления связано с указателем прибора скорости. Когда указатель неподвижен, то перо тоже неподвижно и чертит на движущейся бумаге прямую линию (рис. 12).

Рис. 12. При движении бумаги относительно пера на ней вычерчивается график движения.

Когда же указатель прибора поднимается или опускается, показывая увеличение или уменьшение скорости, то и перо поднимается или опускается, прочерчивая линию на бумаге. Таким образом, перо отмечает на бумаге все изменения скорости.

Если на клетчатой бумаге отметить величины скоростей, (Соответствующие показаниям прибора, то по нашей записи можно будет определить и величину скорости в любой
момент времени.

На рисунке 13 изображена одна из таких записей. На этой записи можно прочитать, что вся поездка длилась 1 час 5 мин. (бумага передвигается на одну клетку за 5 мин.).В первые 5 мин. автомобиль развил скорость в (одно деление по вертикали соответствует скорости ), затем 15 мин. двигался со скоростью К концу 25-й минуты скорость упала до с этой скоростью автомобиль двигался 10 минут, затем скорость начала падать, и автомобиль остановился на 10 мин.
Рис. 13. Пример графика скорости.

После остановки автомобиль за 5 мин. развил скорость до а затем через 10 мин. снова остановился.

Можно автоматически записывать не только скорости движения автомобиля, но и пройденные им пути.

Рис. 14. Пример графика пути.

На рисунке 14 приведена одна из таких записей. По этой записи видно,что через 20 мин. от начала движения автомобиль прошёл 10 км. За следующие 30 мин. автомобиль прошёл 20 км, затем 5 мин. стоял на месте и последние 15 км прошёл за 10 мин.

Такие записи движения, или, как их называют, графики движения, дают наглядное представление об изучаемом движении.

Уравнение равномерного движения

Было установлено, что при равномерном движении пути, проходимые в равные промежутки времени, одинаковы; поэтому при увеличении промежутка времени в несколько раз во столько же раз увеличивается и путь. Так, если за t сек. пройден путь s см, то за 2 t сек. путь будет 2 s см, за 3 t сек.—3 s см и т. д. Скорость v на этих участках пути выразится так:

А это значит, что скорость при равномерном движении одна и та же на всех участках пути.

Итак, можно сказать, что равномерное движение есть движение с постоянной скоростью.

Зная скорость равномерного движения, можно найти путь, пройденный за время t, по формуле:

Написанная формула называется уравнением равномерного движения. Это уравнение математически выражает зависимость пройденного пути от времени: пройденный путь при равномерном движении прямо пропорционален времени.

П р и м е р. Самолёт летит со скоростью Какое расстояние пройдёт самолёт за 1 мин.?

Решая эту задачу по формуле s = vt, мы должны предварительно либо скорость выразить в либо время в часах.

Очевидно, последнее сделать проще, так как 1 мин.=часа; тогда

При решении подобных задач необходимо, чтобы все величины были выражены в надлежащих единицах.

График пути равномерного движения

Зависимость пути от времени при равномерном движении может быть выражена не только алгебраически, в виде формулы, но и чертежом — графически.

Рис. 15. Оси координат (ось времён и ось пройденных путей).

Рис. 16. Построение графика пути равномерного движения.

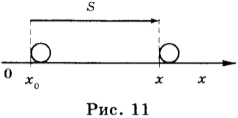
Проведём две взаимно перпендикулярные линии Ot и OS. Эти линии будем называть осями координат (рис. 15), ось Ot — осью времён, а ось OS—осью пройденных путей. Точка О пересечения осей обозначает начало отсчётов и для времени и для пути. Отложим в определённом масштабе как на оси Ot, так и на оси OS равные отрезки. Возьмём где-нибудь на нашем чертеже точку А. Опустим из этой точки перпендикуляры на обе оси. Тогда на оси времён получим отрезок ON, численно равный промежутку времени, а на оси путей — отрезок ОМ, соответствующий пройденному пути. Но ОN = AM, где АМ есть расстояние от точки А до оси пройденных путей, а ОМ = AN — расстояние от точки А до оси времен.

Итак, расстояние, измеряемое от какой-либо точки доноси путей, на чертеже соответствует некоторому промежутку времени, а расстояние от этой точки до оси времён — некоторому пути.

Построим график пути равномерного движения со скоростью По формуле s=vt рассчитаем пройденные в этом движении пути за 1, 2, 3 и т. д. секунды и результаты расчёта запишем в таблицу (стр. 20).

Соответственно данным таблицы на оси времён отложим отрезки, соответствующие 1, 2, 3 секундам (рис. 16). Из концов полученных отрезков проведём перпендикуляры к этой оси и на них отложим пути, пройденные за одну, две и три секунды.

Расстояние между любой точкой этой прямой и осью пройденных путей определит промежуток времени, а расстояние между этой точкой и осью времён — путь, пройденный телом в течение этого промежутка времени.

Так, например, расстояние АМ от точки А (рис. 17) до оси пройденных путей соответствует 2,5 сек., а расстояние AN от той же точки до оси времён — отрезку пути в 5 м, следовательно, за 2,5 сек. пройден путь, равный 5 м.

Рис. 17. График пути равномерного движения.

Рис. 18. Графики путей двух равномерных движений.

На рисунке 18 даны графики путей двух равномерных движений, обозначенные цифрами I и II. Скорость какого из этих движений больше? Чтобы ответить на этот вопрос, возьмём на оси времён промежуток времени, изображённый отрезком ОА. Из конца этого отрезка проведём перпендикуляр до пересечения с нашими графиками. Отрезки этого перпендикуляра АС и АВ определят пути, пройденные в течение одного и того же промежутка времени ОА в обоих движениях.

Так как АС больше АВ, то и скорость первого движения больше скорости второго.

График скорости равномерного движения

Рис. 24. График скорости равномерного движения.

Начертим оси координат и на вертикальной оси будем откладывать отрезки, соответствующие в некотором условном масштабе скоростям движения тела. Назовём эту ось осью скоростей (Ov). На другой же оси (оси времён Ot) будем откладывать отрезки, соответствующие промежуткам времени (рис. 24). Так как скорость равномерного движения не меняется со временем, то график её будет представлять собой прямую линию MN, параллельную оси времён. Если взять на этом графике какую-нибудь точку А,
то отрезок прямой АВ между этой точкой и осью времён будет численно равен скорости данного равномерного движения.

Пользуясь графиком скорости, можно определить и путь, пройденный телом за определённый промежуток времени.

Допустим, что велосипедист движется равномерно со скоростью На рисунке 25 изображён график скорости этого
движения в масштабе: 1 см — 1 см—1 сек.

Чтобы найти путь, пройденный велосипедистом в течение,например, 4 сек., необходимо скорость умножить на время, то есть численное значение отрезка 0—3, отложенного на оси скоростей, помножить на численное значение перпендикулярного к нему отрезка 0—4, отложенного на оси времён. В результате мы получим величину площади заштрихованного прямоугольника. Площадь заштрихованного прямоугольника содержит столько же масштабных единиц площади (малый заштрихованный квадрат), сколько метров проехал велосипедист в течение 4 сек.

Рис. 25. Определение пройденного пути по графику скорости.

Таким образом, на графике скорости равномерного движения численное значение пути равно численному значению площади прямоугольника, одна сторона которого равна скорости движения, а другая— времени движения.

Сложение движений

Движение любого тела можно рассматривать как сложное движение, состоящее из нескольких простых движений. Так, например, движение человека по палубе парохода относительно берега можно рассматривать как сложное движение, состоящее из движения человека ‘относительно парохода и движения парохода относительно берега.

Движения человека относительно парохода и парохода относительно берега называются составляющими движениями, а движение человека относительно берега результирующим движением.

Изучив законы составляющих движений, можно установить и закон результирующего движения.

Определение результирующего движения по данным составляющим движениям называется сложением движений.

Рассмотрим движение лодки по течению. Допустим, что под влиянием усилий гребца лодка перемещается относительно воды со скоростью вода же течет относительно берега со скоростью Какое расстояние пройдёт лодка за время t = 5 час.?

Если бы не было течения, то лодка за 5 час. прошла бы вниз по реке расстояние

Одно же течение перенесло бы лодку на расстояние

Но так как лодку одновременно перемешают и гребец и течение, то за 5 час. она пройдёт вниз по реке расстояние:

s = 20 км + 15 км = 35 км.

Что изменится, если скорости останутся по величине такими же, но гребец будет грести против течения?

Очевидно, что лодка под одновременным действием гребца и течения пройдёт те же расстояния, как и в первом случае, но теперь гребец за 5 час. передвинет лодку на расстояние 20 км вверх по реке, а течение за то же время снесёт лодку на расстояние 15 км вниз. В результате лодка, двигаясь по прямой, за 5 час. пройдёт вверх по реке расстояние:

s = 20 км — 15 км = 5 км.

Если путь вверх по реке считать положительным, а вниз — отрицательным, то можно написать, что

s = 20 км + (— 15 км) = 5 км.

В том и другом случае для нахождения пути сложного движения нужно алгебраически сложить пути составляющих движений.

Если бы на лодку действовал ветер в направлении её движения, то очевидно, что путь, пройденный лодкой за то же время, сложился бы из трёх путей составляющих движений (из пути, пройденного под действием гребца, течения и ветра).

Таким же образом можно найти путь, пройденный телом в сложном движении, состоящем из какого угодно числа равномерных движений, направленных по одной прямой.

Если s —путь результирующего движения, a и т. д.—пути составляющих движений, то можно написать:

При этом пути, пройденные в одном направлении, считаются положительными, а пройденные в противоположном — отрицательными.

Если составляющие движения равномерны, то пройденные пути возрастают пропорционально времени. В этом случае и путь результирующего движения, равный сумме путей составляющих движений, также растёт пропорционально времени. Следовательно, и результирующее движение является также равномерным движением.

Итак, результирующее движение, состоящее из нескольких равномерных прямолинейных движений, есть тоже равномерное прямолинейное движение.

Вычислим, чему равна скорость результирующего движения.

Разделим все члены равенства (1) на время движения:

Ho — скорость результирующего движения, a — скорости слагаемых движений; следовательно, равенство (2) можно написать так:

Скорость результирующего движения, состоящего из равномерных прямолинейных движений, равна алгебраической сумме скоростей составляющих движений.

При этом за положительную скорость принимается скорость такого движения, в направлении которого отсчитываются положительные пути, а отрицательной скорости соответствуют отрицательные пути.

Скорость-вектор

Для определения движения недостаточно знать величину пути, пройденного телом, и величину его скорости. Необходимо знать ещё направление движения. Так, например, чтобы определить, где будет находиться самолёт, вылетевший из Москвы со скоростью 400 через 2 часа, необходимо указать, в каком направлении он летел.

Чтобы полностью определить движение тела, условились указывать направление скорости. Для этого скорость изображают отрезком прямой, совпадающим по направлению с направлением движения тела. Стрелка на конце указывает, в какую сторону по этому направлению движется тело. Длина же отрезка в условном масштабе изображает величину скорости.

Величины, определяемые не только своим численным значением, но и направлением в пространстве, называются векторными величинами, или векторами.

Скорость есть вектор.

Рис. 26. Векторы различных скоростей.

Всякий вектор можно изобразить направленным отрезком. На рисунке 26 направленные отрезки прямой изображают две скорости, различные по величине и по направлению. При изучении физики мы встретимся со многими другими векторными величинами.

В отличие от векторных величин существуют величины, которым нельзя приписать никакого направления в пространстве. Они могут отличаться только величиной и иногда знаком. Такие величины называются скалярными, или скалярами.

К скалярным величинам относятся время, температура, масса, работа, энергия и многие другие величины.

Сложение равномерных прямолинейных движений, направленных под углом друг к другу

В некоторых случаях интересующее нас движение мы можем рассматривать как результат сложения нескольких движений, направленных под углом друг к другу. Таково, например, движение лодки поперёк реки или движение самолёта при боковом ветре.

Рассмотрим на примере движения лодки, каким будет результирующее движение двух равномерных и прямолинейных движений, направленных под углом друг к другу.

Рис. 27. Сложение движений лодки и воды.

Если бы течение отсутствовало, то лодка под влиянием усилий гребца перемещалась бы по направлению ОВ (рис. 27), последовательно переходя через равные промежутки времени в положения, обозначенные на чертеже точками и т. д.

Но течение в те же равные промежутки времени перемещает лодку по прямой ОА в положения, обозначенные на рисунке точками и т. д.

Участвуя одновременно в двух движениях, лодка под влиянием усилий гребца за единицу времени пройдёт путь а течением реки за это же время будет отнесена на расстояние то есть действительное движение лодки относительно берега будет происходить по линии ОС через точки и т. д.

Из рисунка видно, что линия ОС представляет собой диагональ параллелограмма ОВСА, стороны которого ОВ и ОД есть пройденные пути в составляющих движениях. Видно также, что пути, проходимые лодкой вдоль диагонали ОС за равные промежутки времени, равны между собой: следовательно, результирующее движение лодки, происходящее по диагонали параллелограмма, есть движение равномерное и прямолинейное.

Эти выводы, полученные нами при рассмотрении движения лодки, справедливы и для всех случаев, когда тело участвует одновременно в двух движениях. Чтобы в этом убедиться, проделаем опыты.

Рис. 28. Сложное движение шарика, подвешенного на нити.

Закрепим на доске конец нити, на которой подвешен небольшой шарик (рис. 28). Подденем под нить у верхнего её конца карандаш и будем двигать его горизонтально вдоль доски, проходя точки Тогда шарик будет одновременно двигаться вертикально вверх и горизонтально. Относительно же доски он будет перемещаться через точки В, С, D, то есть по диагонали прямоугольника, построенного на составляющих
перемещениях как на сторонах.

Если двигать карандаш не горизонтально, а как-нибудь наклонно, например так, как изображено на рисунке 29, то и в этом случае относительно доски шарик будет перемещаться по диагонали параллелограмма.

Рис, 29. Сложное движение шарика, подвешенного на нити.

Итак, опыт показывает, что если тело участвует одновременно в двух равномерных прямолинейных движениях, направленных под углом друг к другу, то результирующее движение его будет равномерное и прямолинейное. Пройденный путь в этом движении изображаете я диагональю параллелограмма, построенного на пройденных путях составляющих движений как на сторонах.

Сложение скоростей

От сложения движений легко перейти к сложению скоростей. Обратимся к рисунку 30.

Рис. 30. Сложение скоростей.

Пусть стороны параллелограмма представляют собой пройденные пути и двух одновременно происходящих равномерных прямолинейных движений за один и тот же промежуток времени, а диагональ параллелограмма — пройденный путь s результирующего движения. Если пройденные пути разделить на время движения t, то получим скорости соответствующих движений:

и

Мы знаем, что направление скорости прямолинейного движения совпадает с
направлением движения (§ 13). Из точки О отложим на направлениях движений векторы этих скоростей. Соединив концы векторов и с концом вектора v прямыми линиями, мы получим параллелограмм

Следовательно, скорость результирующего движения по величине и направлению изображается диагональю параллелограмма, построенного на скоростях составляющих движений как на сторонах.

Этот вывод называется правилом параллелограмма скоростей.

Правило параллелограмма справедливо не только для скоростей, но и для всяких векторов.

Разложение скорости

На рисунке 31 изображён самолёт, поднимающийся вверх под некоторым углом к горизонту со скоростью v.

Допустим, что нам необходимо узнать, с какой скоростью самолёт поднимается вертикально вверх и с какой скоростью он движется в горизонтальном направлении. Представим скорость самолёта, состоящей из скорости, направленной горизонтально, и скорости, направленной вертикально. Для этого воспользуемся правилом параллелограмма. Пусть диагональ в этом параллелограмме изображает вектор скорости самолёта v.

Из начала вектора v проводим две взаимно перпендикулярные линии, одну в вертикальном, другую в горизонтальном направлении. Затем из конца этого вектора проводим линии, параллельные двум заданным направлениям. Они отсекут отрезки, численные значения которых будут равны горизонтальной составляющей скорости и вертикальной

Нахождение по данной скорости её составляющих называется разложением скорости.

Разложение скорости на составляющие обратно действию сложения скоростей.

Так как любую скорость можно рассматривать как результирующую скорость, то, следовательно, любую скорость можно разложить на составляющие.

Важно подчеркнуть, что данную скорость можно представить в виде диагонали множества параллелограммов с различными сторонами. Следовательно, данную скорость можно разложить на множество пар различных скоростей. В практике чаще всего встречаются случаи разложения скорости на две взаимно перпендикулярные составляющие. Такая задача и была решена нами.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник