How to find vertex of parabola
How to find vertex of parabola
Vertex of a Parabola Formula
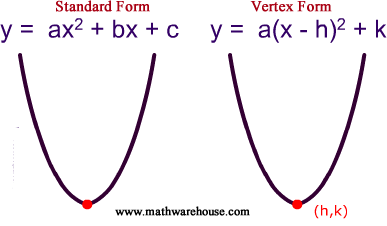
The point where the parabola and its axis of symmetry intersect is called the vertex of a parabola. It is used to determine the coordinates of the point on the parabola’s axis of symmetry where it crosses it. For standard equation of a parabola y = ax 2 + bx + c, the vertex point is the coordinate (h, k). If the coefficient of x 2 in the equation is positive (a > 0), then vertex lies at the bottom else it lies on the upper side.
Vertex formula
For the vertex form of the parabola, y = a(x – h) 2 + k, the coordinates (h, k) of the vertex are,
b is the coefficient of x,
D = b 2 – 4ac is the discriminant of the standard form y = ax 2 + bx + c.
Derivation
Suppose we have a parabola with standard equation as, y = ax 2 + bx + c.
This can be written as,
y – c = a (x 2 + bx/a)
Adding and subtracting b 2 /4a 2 on the RHS, we get
y – c = a (x 2 + bx/a + b 2 /4a 2 – b 2 /4a 2 )
y – c = a ((x + b/2a) 2 – b 2 /4a 2 )
y – c = a (x + b/2a) 2 – b 2 /4a
y = a (x + b/2a) 2 – b 2 /4a + c
y = a (x + b/2a) 2 – (b 2 /4a – c)
y = a (x + b/2a) 2 – (b 2 – 4ac)/4a
We know, D = b 2 – 4ac, so the equation becomes,
y = a (x + b/2a) 2 – D/4a
Comparing the above equation with the vertex form y = a(x – h) 2 + k, we get
This derives the formula for coordinates of the vertex of a parabola.
Sample Problems
Problem 1. Find the coordinates of the vertex for the parabola y = 2x 2 + 4x – 4.
Solution:
We have the equation as, y = 2x 2 + 4x – 4.
Problem 2. Find the coordinates of the vertex for the parabola y = 3x 2 + 5x – 2.
Solution:
We have the equation as, y = 3x 2 + 5x – 2.
Problem 3. Find the coordinates of the vertex for the parabola y = 3x 2 – 6x + 1.
Solution:
We have the equation as, y = 3x 2 – 6x + 1.
So, x – coordinate of vertex = 6/2(3) = 6/6 = 1
Problem 4. Find the coordinates of the vertex for the parabola y = 3x 2 + 8x – 8.
Solution:
We have the equation as, y = 3x 2 + 8x – 8.
Problem 5. Find the coordinates of the vertex for the parabola y = 6x 2 + 12x + 4.
Solution:
We have the equation as, y = 6x 2 + 12x + 4.
Here, a = 6, b = 12 and c = 4.
Problem 6. Find the coordinates of the vertex for the parabola y = x 2 + 7x – 5.
Solution:
We have the equation as, y = x 2 + 7x – 5.
Problem 7. Find the coordinates of the vertex for the parabola y = 2x 2 + 10x – 3.
Solution:
We have the equation as, y = x2 + 7x – 5.
SAT / ACT Prep Online Guides and Tips
Vertex Form: What Is It? How Do You Calculate It?
Once you have the quadratic formula and the basics of quadratic equations down cold, it’s time for the next level of your relationship with parabolas: learning about their vertex form.
Read on to learn more about the parabola vertex form and how to convert a quadratic equation from standard form to vertex form.
feature image credit: SBA73/Flickr
Why Is Vertex Form Useful? An Overview
The vertex form of an equation is an alternate way of writing out the equation of a parabola.
If you need to find the vertex of a parabola, however, the standard quadratic form is much less helpful. Instead, you’ll want to convert your quadratic equation into vertex form.
What Is Vertex Form?
In this case, this means:
Parabola Vertex Form
Vertex Coordinates
How to Convert From Standard Quadratic Form to Vertex Form
Most of the time when you’re asked to convert quadratic equations between different forms, you’ll be going from standard form ($ax^2+bx+c$) to vertex form ($a(x-h)^2+k$).
The process of converting your equation from standard quadratic to vertex form involves doing a set of steps called completing the square. (For more about completing the square, be sure to read this article.)
What we need to do now is the hardest part—completing the square.
To set this up (and make sure we don’t forget to add the constant to the other side of the equation), we’re going to create a blank space where the constant will go on either side of the equation:
The next step is to complete the square. In this case, the square you’re completing is the equation inside of the parentheses—by adding a constant, you’re turning it into an equation that can be written as a square.
$(6/2)^2=(3)^2=9$. The constant is 9.
Now, replace the blank space on either side of our equation with the constant 9:
Last step: move the non-$y$ value from the left side of the equation back over to the right side:
Congratulations! You’ve successfully converted your equation from standard quadratic to vertex form.
Now, most problems won’t just ask you to convert your equations from standard form to vertex form; they’ll want you to actually give the coordinates of the vertex of the parabola.
To avoid getting tricked by sign changes, let’s write out the general vertex form equation directly above the vertex form equation we just calculated:
Whew, that was a lot of shuffling numbers around! Fortunately, converting equations in the other direction (from vertex to standard form) is a lot simpler.
How to Convert From Vertex Form to Standard Form
Converting equations from their vertex form to the regular quadratic form is a much more straightforward process: all you need to do is multiply out the vertex form.
Parabola Vertex Form Practice: Sample Questions
To wrap up this exploration of vertex form, we have four example problems and explanations. See if you can solve the problems yourself before reading through the explanations!
Parabola Vertex Form Practice: Solutions
Start by separating out the non-$x$ variable onto the other side of the equation:
Factor the right side of the equation inside the parentheses:
Finally, combine the constants on the left side of the equation, then move them over to the right side.
Next, bring the constant over to the left side of the equation:
Now to find the vertex:
Now, there are a couple of ways to go from here. The sneaky way is to use the fact that there’s already a square written into the vertex form equation to our advantage.
First, we’ll move the constant over to the left side of the equation:
Next, we’ll divide both sides of the equation by 2:
Now, the sneaky part. Take the square root of both sides of the equation:
Have friends who also need help with test prep? Share this article!
Laura graduated magna cum laude from Wellesley College with a BA in Music and Psychology, and earned a Master’s degree in Composition from the Longy School of Music of Bard College. She scored 99 percentile scores on the SAT and GRE and loves advising students on how to excel in high school.
Student and Parent Forum
Our new student and parent forum, at ExpertHub.PrepScholar.com, allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.
Ask a Question Below
Have any questions about this article or other topics? Ask below and we’ll reply!
Vertex of a Parabola
Before going to learn what is the vertex of a parabola, let us recall what is a parabola. A parabola is basically a ‘U’ shaped curve turned in different directions. It can be in one of the 4 forms.
Every parabola has a turning point. i.e., it has a point where it either changes from «increasing» to «decreasing» or vice versa. That turning point is called the vertex of the parabola. Let us learn more about the vertex of a parabola along with the different processes of finding it.
| 1. | What is Vertex of a Parabola? |
| 2. | Vertex of a Parabola Formula |
| 3. | Finding Vertex of a Parabola From Standard Form |
| 4. | Finding Vertex of a Parabola From Vertex Form |
| 5. | Finding Vertex of a Parabola From Intercept Form |
| 6. | Properties of Vertex of a Parabola |
| 7. | FAQs on Vertex of a Parabola |
What is Vertex of a Parabola?
The vertex of a parabola is a point at which the parabola makes its sharpest turn. A parabolic function has either a maximum value (if it is of the shape ‘∩’) or a minimum value (if it is of the shape ‘U»). The vertex of a parabola is also the point of intersection of the parabola and its axis of symmetry.
Different Types of Parabolas
There can be two types of equations of a parabola which represent 4 different types of parabolas. The equation of any parabola involves a quadratic polynomial.
Top/Bottom Opened Parabolas:
The equation of a top/bottom opened parabola can be in one of the following three forms:
Finding Vertex of a Parabola From Standard Form
We know that the equation of a parabola in standard form can be either of the form y = ax 2 + bx + c (up/down) or of the form x = ay 2 + by + c (left/right). Let us see the steps to find the vertex of the parabola in each case.
Vertex of a Top/Bottom Opened Parabola
Vertex of a Left/RightOpened Parabola
Finding Vertex of a Parabola From Vertex Form
Vertex of a Top/Bottom Opened Parabola
Vertex of a Left/RightOpened Parabola
Finding Vertex of a Parabola From Intercept Form
Vertex of a Top/Bottom Opened Parabola
Vertex of a Left/Right Opened Parabola
Properties of Vertex of a Parabola
Here are some properties of the vertex of a parabola that follow from the definition of the vertex of a parabola.
Important Notes Related to Vertex of a Parabola:
Topics Related to Vertex of a Parabola:
Examples on Vertex of a Parabola
Solution:
We know that y = ax 2 + bx + c
Here a = 3 > 0 and hence it has a minimum at its vertex.
b) By comparing y = (-1/2)x 2 + 7 with y = ax 2 + bx + c, we get a = (-1/2).
Here a = (-1/2) 2 + 3x + 4.
Solution:
Comparing the given equation with y = ax 2 + bx + c, we have a = 0.5, b = 3, and c = 4.
Solution:
Equation of a Parabola
Standard Form and Vertex Form Equations
The equation of a parabola can be expressed in either standard or vertex form as shown in the picture below.
Standard Form Equation
The standard form of a parabola’s equation is generally expressed:
The vertex form of a parabola’s equation is generally expressed as: y = a(x-h) 2 +k
Practice Problems
Vertex and Direction-Vertex Form Equation
Part I
Problem 1
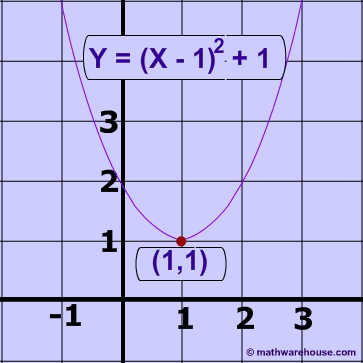
What is the graph of the following parabola y = (x–1)² + 1?
The parabola’s vertex is the point (1,1).
Problem 2
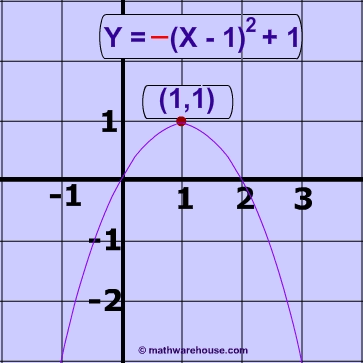
What is the graph of the following parabola y = –(x–1)² + 1?
Problem 3
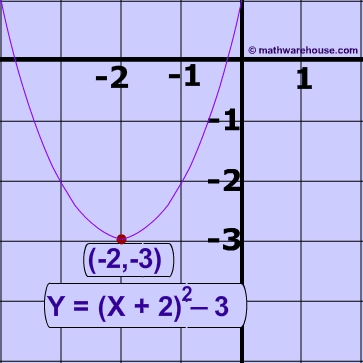
What is the graph of the following parabola y = (x+2)² –3?
Identifying the vertex in vertex form
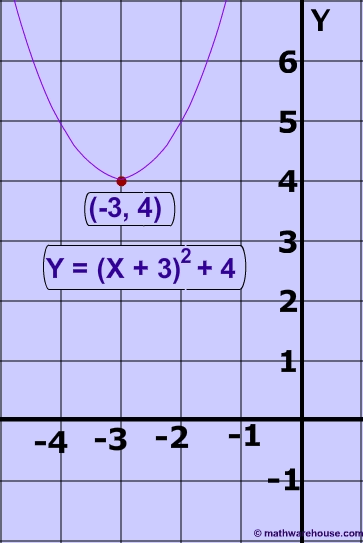
Problem 4.1
What is the vertex of the following parabola: y = (x + 3)² + 4
The vertex is the point (-3,4)
Problem 4.2
Problem 4.3
Part II
Problem 5.1
What is the vertex of a parabola with the following equation:
y = 2(x-3) 2 +4? Does the parabola open upwards or downwards?
The vertex is (3,4) and it opens upwards since a is positive( it is 2), it opens upwards.
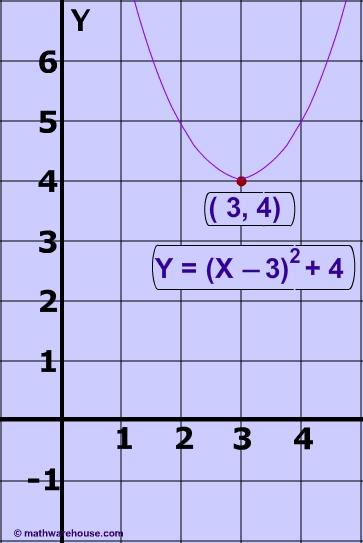
Problem 5.2
If a parabola’s equation is y = 3(x+3) 2 +4, what is its vertex? Which way does it open?
Vertex = (-3, 4), and it opens upwards since a is positive.
Problem 5.3
How to Graph a Parabola
This article was co-authored by Jake Adams. Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
There are 8 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 261,784 times.
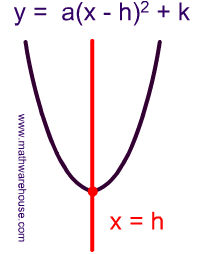
A parabola is a graph of a quadratic function and it’s a smooth «U» shaped curve. Parabolas are also symmetrical which means they can be folded along a line so that all of the points on one side of the fold line coincide with the corresponding points on the other side of the fold line. The fold line, called the axis of symmetry, is the vertical line that goes through the verex. [1] X Expert Source
Jake Adams
Academic Tutor & Test Prep Specialist Expert Interview. 20 May 2020. Any point on the parabola is equidistant from a fixed point (the focus) and a fixed straight line (the directrix). In order to graph a parabola, you need to find its vertex as well as several points on either side of the vertex in order to mark the path that the points travel.