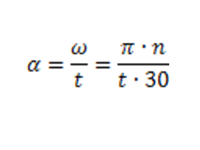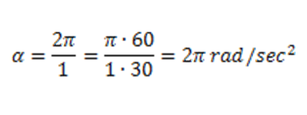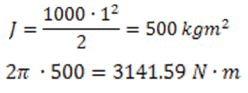How to find the angle using angular acceleration and normal acceleration
How to find the angle using angular acceleration and normal acceleration
How to find the angle using angular acceleration and normal acceleration
Posted by Niilo Nykanen on Fri, Jun 14, 2013 @ 14:22 PM
Angular Acceleration and Moment of Inertia in Machine Design
As a provider of flexible drive couplings and ball detent safety clutches, we are often asked to provide a bit of assistance in calculating application torques, especially for customers looking to retrofit existing equipment. In order to aid in the process of estimating torques, we’ll review one of the basic calculations used to estimate the torque required to accelerate a rotating mass to a certain speed over a given time.
Angular acceleration (α) can be defined as angular velocity (ω) divided by acceleration time (t). Alternatively, pi (π) multiplied by drive speed (n) divided by acceleration time (t) multiplied by 30. This equation yields the standard angular acceleration SI unit of radians per second squared (Rad/sec^2). The equation below defines the rate of change of angular velocity.
ω = angular velocity in the standard SI unit of radians per second (Rad/sec), 1 radian = 57.3 degrees
t = acceleration time in seconds
n = drive speed in revolutions per minute RPM
In the next example, angular velocity will be calculated for acceleration from 0 to 60 RPM in one second. Note that 2π radians per second = 60 RPM.
This calculation is very useful in machine design because angular acceleration multiplied by rotational moment of inertia equals torque. Keep in mind that the exact moment of inertia can be difficult to calculate based on complex geometries in real drive lines, and other variables such as friction are not considered in the next calculation. Nonetheless it is still very helpful in approximating torque requirements or establishing baseline minimum values for component sizing purposes.
J = moment of inertia in kg∙m 2
N= force in Newtons
kg= mass in kilograms
m= lever arm radius in meters
In the final example below we will use the angular acceleration we found above to calculate torque on a flywheel with a 1 meter radius and 1000 kg mass.
As we can see, if a flywheel with a 1 meter radius and 1000 kg mass were to be accelerated to 60 RPM in one second, it would require 3141.59 Newton meters of input torque.
I hope you found this refresher on calculating angular acceleration to be helpful. If you have questions pertinent to the sizing and application of shaft couplings or safety clutches, feel free to contact our applications engineering department.
How to find the angle using angular acceleration and normal acceleration
Rotational motion
The sections on rotational motion are best tackled in this order:
You might also want to refresh your memory about units of angle measurement, degrees and radians.
Angular acceleration
Angular acceleration is any change in the angular velocity vector. That means an increase in angular velocity, a decrease in angular velocity, or a change of direction of the angular velocity vector.
Recall that the angular velocity vector lies along the axis of rotation (at a right angle to the rotational plane) and, by convention, follows the right hand rule.
In this section, we’ll consider both angular acceleration and centripetal acceleration.
The Greek alphabet
| alpha | Α | α |
| beta | Β | β |
| gamma | Γ | γ |
| delta | Δ | δ |
| epsilon | Ε | ε |
| zeta | Ζ | ζ |
| eta | Η | η |
| theta | Θ | θ |
| iota | Ι | ι |
| kappa | Κ | κ |
| lambda | Λ | λ |
| mu | Μ | μ |
| nu | Ν | ν |
| xi | Ξ | ξ |
| omicron | Ο | ο |
| pi | Π | π |
| rho | Ρ | ρ |
| sigma | Σ | σ |
| tau | Τ | τ |
| upsilon | Υ | υ |
| phi | Φ | φ |
| chi | Χ | χ |
| psi | Ψ | ψ |
| omega | Ω | ω |
The math of angular acceleration
Angular acceleration is the change in angular velocity over time.
As defined, the angular acceleration is the average angular acceleration, which we denote by placing a bar over the alpha:
Of course, the average accleration can also be determined by simply taking the numerical average of two accelerations, assuming a smooth transition from one to the next:
The instantaneous angular acceleration is the limit of Δω/Δt as Δt approaches zero:
If you know a little differential calculus, this is just the first derivative of the angular velocity, Δ with respect to time.
And finally, because angular velocity is the first derivative of the angle with respect to time, angular acceleration is the second derivative.
SI units
SI stands for SystГЁme international (of units). In 1960, the SI system of units was published as a guide to the preferred units to use for a variety of quantities. Here are some common SI units
| length | meter | (m) |
| mass | Kilogram | (Kg) |
| time | second | (s) |
| force | Newton | N |
| energy | Joule | J |
Relationship to linear acceleration
To find the linear acceleration of an object traveling in a circle (also called tangential acceleration because the vector is always tangent to the circle), we can step back to an earlier development of linear velocity from angular velocity.
The arc S can be determined simply if we work in radians. We simply set up the proportion: «The angle θ is to a full circle (2π) as the arc S is to the full circumference (2πr):
The 2π‘s cancel, giving the angle in terms of the arc length and radius.
Now the average angular velocity is:
In the last step we substituted S/r for θ. Now we showed that
Therefore the angular velocity is related to the velocity (average or instantaneous) by:
Now angular acceleration is the change in angular velocity over time,
So we can combine that with the previous result to get:
Note that r is constant, so we can exempt it from the delta (it doesn’t change). Substituting linear acceleration for Δv/Δt, we get the relationship between angular and linear or tangential acceleration:
Centripetal acceleration
Let’s insert here a few comments about centripetal acceleration, the only acceleration needed to keep a turning body turning.
You are familiar with the feeling of going around a corner as a passenger in a car, and feeling like if the door wasn’t there, you’d fly out of the car (you would). That’s often confused with an outward force (away from the axis of rotation), but no such force exists. Such a «centrifugal» force is a pseudo-force. It’s not a real force, only the impression of one that really stems from the centripetal or «center-seeking» force.
What you’re feeling when you’re going around that corner is the car pushing you into the turn. Without the car there to push on you, you’d continue in the path of your inertia, which is a straight line tangent to the curve. The figure here illustrates that.
A body, like the green circle in the figure, has centripetal acceleration just because it is moving in a circle, because its velocity vector is always changing direction.
If its velocity vector is also changing in length, then it is accelerating tangentially, too. Otherwise it has no linear or tangential acceleration.
Practice problems
$$\omega = \alpha t = 0.75 \, \frac$$
For (b), in order to find the number of rotations, we’ll need the average angular velocity over those 60 seconds, which is just the average of the starting and ending angular velocities:
Now the number of radians is
If we divide 2π radians into that, we get the number of full rotations:
Now for the linear velocity at the rotor tips:
$$v = r\omega = (7.25 \, m)\left( 45 \frac\right) = 326 \, \frac$$
That’s just below the speed of sound (
340 m/s). Generally, helicopters keep the blade-end speed below the speed of sound, where strange things happen and the machine can lose a lot of power.
The inital angular velocity in rad/s is
Now the definition of angular acceleration can be rearranged to find the time:
A washing machine spins clothes to near dryness. If it begins spinning at 20 rad/s and slows down to 7 rad/s while turning through 500 revolutions,
We’ll need the average angular velocity, which is just the numerical average of 20 and 7 rad/s:
We can convert this to revolutions per second:
Now if we divide 500 revolutions by that number of revolutions per second (just pay attention to the units), we get the time that it takes for 500 revolutions:
That’s 3:53 in minutes:seconds. Now we have all we need to calculate the angular accleration:
A centrifuge starts from rest and reaches an angular velocity of 30,000 rpm in 5 seconds. Calculate the angular acceleration (in rad/s 2 ) of this device. If the radius of the rotor (the part that spins in a centrifuge) is 10 cm, what is the linear velocity, in miles per hour, of the outside of the rotor?
First convert revolutions per minute (rpm) into radians per second:
Now calculate the angular accleration:
$$v = 0.01 \, m \left( 3141 \frac\right) = 31.41 \, \frac$$
Finally, convert to mi./h, where 1 mile = 1609 meters and 1 hour = 3600 s.
A flywheel rotating at 2.0 rpm undergoes an angular acceleration of 2.0 rad/s 2 for five revolutions. Calculate the angular velocity of the flywheel at the end of this acceleration.
The time to spin up to the final angular velocity is then
xaktly.com by Dr. Jeff Cruzan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. © 2012, Jeff Cruzan. All text and images on this website not specifically attributed to another source were created by me and I reserve all rights as to their use. Any opinions expressed on this website are entirely mine, and do not necessarily reflect the views of any of my employers. Please feel free to send any questions or comments to jeff.cruzan@verizon.net.
How to find the angle using angular acceleration and normal acceleration
By the end of this section, you will be able to:
In the preceding section, we defined the rotational variables of angular displacement, angular velocity, and angular acceleration. In this section, we work with these definitions to derive relationships among these variables and use these relationships to analyze rotational motion for a rigid body about a fixed axis under a constant angular acceleration. This analysis forms the basis for rotational kinematics. If the angular acceleration is constant, the equations of rotational kinematics simplify, similar to the equations of linear kinematics discussed in Motion along a Straight Line and Motion in Two and Three Dimensions. We can then use this simplified set of equations to describe many applications in physics and engineering where the angular acceleration of the system is constant. Rotational kinematics is also a prerequisite to the discussion of rotational dynamics later in this chapter.
Kinematics of Rotational Motion
To begin, we note that if the system is rotating under a constant acceleration, then the average angular velocity follows a simple relation because the angular velocity is increasing linearly with time. The average angular velocity is just half the sum of the initial and final values:
From the definition of the average angular velocity, we can find an equation that relates the angular position, average angular velocity, and time:
Solving for [latex] \theta [/latex], we have
where we have set [latex]
We rearrange this to get [latex] \alpha dt=d\omega [/latex] and then we integrate both sides of this equation from initial values to final values, that is, from [latex]
Setting [latex]
We rearrange this to obtain
where [latex] <\omega >_ <0>[/latex] is the initial angular velocity. (Figure) is the rotational counterpart to the linear kinematics equation [latex]
Let’s now do a similar treatment starting with the equation [latex] \omega =\frac
where we have set [latex]
(Figure) is the rotational counterpart to the linear kinematics equation found in Motion Along a Straight Line for position as a function of time. This equation gives us the angular position of a rotating rigid body at any time t given the initial conditions (initial angular position and initial angular velocity) and the angular acceleration.
We can find an equation that is independent of time by solving for t in (Figure) and substituting into (Figure). (Figure) becomes
(Figure) through (Figure) describe fixed-axis rotation for constant acceleration and are summarized in (Figure).
| Angular displacement from average angular velocity | [latex] <\theta >_<\text |
| Angular velocity from angular acceleration | [latex] <\omega >_<\text |
| Angular displacement from angular velocity and angular acceleration | [latex] <\theta >_<\text |
| Angular velocity from angular displacement and angular acceleration | [latex] <\omega >_<\text |
Applying the Equations for Rotational Motion
Now we can apply the key kinematic relations for rotational motion to some simple examples to get a feel for how the equations can be applied to everyday situations.
Example
Calculating the Acceleration of a Fishing Reel
A deep-sea fisherman hooks a big fish that swims away from the boat, pulling the fishing line from his fishing reel. The whole system is initially at rest, and the fishing line unwinds from the reel at a radius of 4.50 cm from its axis of rotation. The reel is given an angular acceleration of [latex] 110<\,\text
(a) What is the final angular velocity of the reel after 2 s?
(b) How many revolutions does the reel make?
Figure 10.11 Fishing line coming off a rotating reel moves linearly.
Strategy
Identify the knowns and compare with the kinematic equations for constant acceleration. Look for the appropriate equation that can be solved for the unknown, using the knowns given in the problem description.
Solution
Converting radians to revolutions gives
Significance
This example illustrates that relationships among rotational quantities are highly analogous to those among linear quantities. The answers to the questions are realistic. After unwinding for two seconds, the reel is found to spin at 220 rad/s, which is 2100 rpm. (No wonder reels sometimes make high-pitched sounds.)
In the preceding example, we considered a fishing reel with a positive angular acceleration. Now let us consider what happens with a negative angular acceleration.
Example
Calculating the Duration When the Fishing Reel Slows Down and Stops
Strategy
We are asked to find the time t for the reel to come to a stop. The initial and final conditions are different from those in the previous problem, which involved the same fishing reel. Now we see that the initial angular velocity is [latex] <\omega >_<0>=220\,\text[/latex] and the final angular velocity [latex] \omega [/latex] is zero. The angular acceleration is given as [latex] \alpha =-300\,<\text
Solution
The equation states
We solve the equation algebraically for t and then substitute the known values as usual, yielding
Significance
Note that care must be taken with the signs that indicate the directions of various quantities. Also, note that the time to stop the reel is fairly small because the acceleration is rather large. Fishing lines sometimes snap because of the accelerations involved, and fishermen often let the fish swim for a while before applying brakes on the reel. A tired fish is slower, requiring a smaller acceleration.
Check Your Understanding
A centrifuge used in DNA extraction spins at a maximum rate of 7000 rpm, producing a “g-force” on the sample that is 6000 times the force of gravity. If the centrifuge takes 10 seconds to come to rest from the maximum spin rate: (a) What is the angular acceleration of the centrifuge? (b) What is the angular displacement of the centrifuge during this time?
b. Using (Figure), we have
Example
Angular Acceleration of a Propeller(Figure) shows a graph of the angular velocity of a propeller on an aircraft as a function of time. Its angular velocity starts at 30 rad/s and drops linearly to 0 rad/s over the course of 5 seconds. (a) Find the angular acceleration of the object and verify the result using the kinematic equations. (b) Find the angle through which the propeller rotates during these 5 seconds and verify your result using the kinematic equations.
Figure 10.12 A graph of the angular velocity of a propeller versus time.
Strategy
Then we use the kinematic equations for constant acceleration to verify the result.
Solution
Figure 10.13 The area under the curve is the area of the right triangle.
We verify the solution using (Figure):
Setting [latex] <\theta >_<0>=0 [/latex], we have
This verifies the solution found from finding the area under the curve.
Significance
We see from part (b) that there are alternative approaches to analyzing fixed-axis rotation with constant acceleration. We started with a graphical approach and verified the solution using the rotational kinematic equations. Since [latex] \alpha =\frac
Summary
Conceptual Questions
If a rigid body has a constant angular acceleration, what is the functional form of the angular velocity in terms of the time variable?
straight line, linear in time variable
If a rigid body has a constant angular acceleration, what is the functional form of the angular position?
If the angular acceleration of a rigid body is zero, what is the functional form of the angular velocity?
A massless tether with a masses tied to both ends rotates about a fixed axis through the center. Can the total acceleration of the tether/mass combination be zero if the angular velocity is constant?
Problems
A wheel has a constant angular acceleration of [latex] 5.0\,\text>^ <2>[/latex]. Starting from rest, it turns through 300 rad. (a) What is its final angular velocity? (b) How much time elapses while it turns through the 300 radians?
a. [latex] \omega =54.8\,\text[/latex];
b. [latex] t=11.0\,\text [/latex]
During a 6.0-s time interval, a flywheel with a constant angular acceleration turns through 500 radians that acquire an angular velocity of 100 rad/s. (a) What is the angular velocity at the beginning of the 6.0 s? (b) What is the angular acceleration of the flywheel?
The angular velocity of a rotating rigid body increases from 500 to 1500 rev/min in 120 s. (a) What is the angular acceleration of the body? (b) Through what angle does it turn in this 120 s?
b. [latex] \theta =66,264\,\text
A flywheel slows from 600 to 400 rev/min while rotating through 40 revolutions. (a) What is the angular acceleration of the flywheel? (b) How much time elapses during the 40 revolutions?
A wheel 1.0 m in diameter rotates with an angular acceleration of [latex] 4.0\,\text>^ <2>[/latex]. (a) If the wheel’s initial angular velocity is 2.0 rad/s, what is its angular velocity after 10 s? (b) Through what angle does it rotate in the 10-s interval? (c) What are the tangential speed and acceleration of a point on the rim of the wheel at the end of the 10-s interval?
a. [latex] \omega =42.0\,\text[/latex];
A vertical wheel with a diameter of 50 cm starts from rest and rotates with a constant angular acceleration of [latex] 5.0\,\text>^ <2>[/latex] around a fixed axis through its center counterclockwise. (a) Where is the point that is initially at the bottom of the wheel at [latex] t=10\,\text
A circular disk of radius 10 cm has a constant angular acceleration of [latex] 1.0\,\text>^ <2>[/latex]; at [latex] t=0 [/latex] its angular velocity is 2.0 rad/s. (a) Determine the disk’s angular velocity at [latex] t=5.0\,\text [/latex]. (b) What is the angle it has rotated through during this time? (c) What is the tangential acceleration of a point on the disk at [latex] t=5.0\,\text? [/latex]
a. [latex] \omega =7.0\,\text[/latex];
The angular velocity vs. time for a fan on a hovercraft is shown below. (a) What is the angle through which the fan blades rotate in the first 8 seconds? (b) Verify your result using the kinematic equations.
A rod of length 20 cm has two beads attached to its ends. The rod with beads starts rotating from rest. If the beads are to have a tangential speed of 20 m/s in 7 s, what is the angular acceleration of the rod to achieve this?
Angular Displacement, Velocity and Acceleration
Introduction
Up to this point, we have considered motion of an object in either a straight line or a curved line as though the object had all its mass concentrated at one point. However, most objects in the real world have a physical size larger than zero, and in addition, in the motion of the object through space, we must consider the possibility that the object will rotate around some axis.
In studying rotation, we will proceed much as we did with linear motion. First we will learn how to describe rotation, a kind of rotational kinematics. We will then examine the causes of rotation, a kind of rotational dynamics. Finally we will apply our understanding of rotational motion to a special kind of motion called «Simple Harmonic Motion (SHM).
Angular Displacement
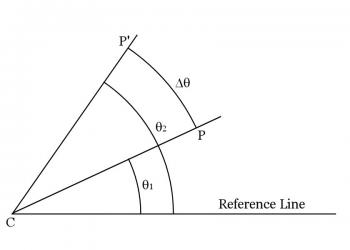
In the following discussion, refer to Figure 6.2.1 below. Consider an object which is free to rotate about some point, C, which we may call the axis of rotation. Let P be a second point located somewhere on the object other than the point C. The line drawn from C to P will be called the radius of the point P. Now draw a line, fixed in space, which we will refer to as the reference line. The angle between the reference line and the radius line will be labeled θ. This angle gives the angular position of the object with reference to the fixed line. It corresponds to the position of an object on the x axis, X, as discussed in the kinematics chapter.
Now let the object rotate around the point C. At one point in time the object might be located so its angular position is given by θ1. At a later instant, it might be moved so its angular position is given by θ2. The change in angular position is the difference between the two angles, labeled Δθ (delta theta, or «change in theta») in the diagram.
Angular Position, Velocity and Acceleration
An article has already been written about linear motion along a straight line. You may want to consider reading that article first. Here we discuss rotational motion, the motion when a body rotates about an axis.
Angular Position
In straight line motion we draw a xy-plane with x and y-axis and consider the motion of a particle along x or y-axis. Similarly here in angular motion of a particle we consider a particle moving in a circle but this time the circle is parallel to the xy-plane (i.e. the circle lies on the plane ) and remains perpendicular to z-axis.
We consider one diameter of the circle along x-axis and another diameter along y-axis such that both diameters are perpendicular to each other as in Figure 1 where z-axis is towards you (you are reading this on either a computer screen or a smartphone).
Figure 3 A particle moves in clockwise direction in a circle.
Here you may have noticed that the position of the particle is measured by the angle made by the line joining the particle and the origin called angular position or angular displacement. In angular displacement the angle has either clockwise or anticlockwise direction but if we say angular distance, we neglect angular direction and focus on the magnitude only.
Angular Velocity
As in linear velocity which was the rate of change of linear displacement, the angular velocity is the rate of change of angular displacement.
In figures Figure 2 and Figure 3 the circle along which the particle moves lies on the xy-plane perpendicular to z-axis. The z-axis is not shown in Figure 2 and Figure 3 which is perpendicular to the xy-plane and passes through the origin.
The direction of angular velocity is determined by the right hand rule- curl the fingers of your right hand in the direction of rotation leaving the thumb straight along the axis (in our case z-axis) perpendicular the plane of rotation (in our case xy-plane) and the thumb gives the direction.
If the particle is moving in anticlockwise direction, you should curl your fingers of right hand in anticlockwise direction leaving the thumb straight (in our case the thumb should be along z-axis) and the thumb gives the direction of angular velocity.
Angular Acceleration
If the particle’s linear speed increases (in clockwise or anticlockwise direction), the angular velocity and acceleration both lie in the same direction but on the other hand if the particle’s linear speed decreases, the angular velocity and acceleration lie in opposite directions.
One easy idea to remember the direction of angular acceleration is that first find the direction of angular velocity by the right hand thumb rule and check whether the particle is speeding up or slowing down.
If you find the particle is speeding up, the direction of angular acceleration will be the same as the direction of angular velocity but if you find the particle is slowing down, the direction of angular acceleration will be opposite to the direction of angular velocity. Another important thing you should remember is the speed is always a positive quantity and it doesn’t matter what the direction of motion is.
Linear and Angular Speeds
As said above the speed is a positive quantity- it can’t be negative. Here we derive an expression that connects linear speed of a particle rotating about a point with its angular speed.
Figure 4 An angle radian is the ratio of arc length to radius of a circle. 
Figure 5 A particle has both tangential and centripetal components of acceleration.
\[s = r\theta \tag <5>\label<5>\]
\[v = r\omega \tag <6>\label<6>\]
Источники информации:
- http://xaktly.com/AngularAcceleration.html
- http://courses.lumenlearning.com/suny-osuniversityphysics/chapter/10-2-rotation-with-constant-angular-acceleration/
- http://www.theproblemsite.com/reference/science/physics/study-guide/rotational-shm/angular-displacement-velocity-acceleration
- http://www.physicskey.com/20/angular-position-velocity-and-acceleration