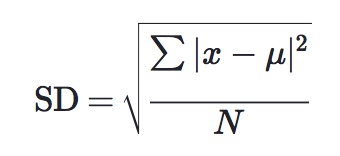How to find standard deviation
How to find standard deviation
SAT / ACT Prep Online Guides and Tips
How to Find Standard Deviation: Simple 6-Step Formula
Standard deviation is a way to calculate how spread out data is. You can use the standard deviation formula to find the average of the averages of multiple sets of data.
Confused by what that means? How do you calculate standard deviation? Don’t worry! In this article, we’ll break down exactly what standard deviation is and how to find standard deviation.
What Is Standard Deviation?
Standard deviation is a formula used to calculate the averages of multiple sets of data. Standard deviation is used to see how closely an individual set of data is to the average of multiple sets of data.
There are two types of standard deviation that you can calculate:
Population standard deviation is when you collect data from all members of a population or set. For population standard deviation, you have a set value from each person in the population.
Sample standard deviation is when you calculate data that represents a sample of a large population. In contrast to population standard deviation, sample standard deviation is a statistic. You’re only taking samples of a larger population, not using every single value as with population standard deviation.
Standard Deviation Formula: How to Find Standard Deviation (Population)
Here’s how you can find population standard deviation by hand:
That’s a lot to remember! You can also use a standard deviation formula.
The commonly used population standard deviation formula is:
In this formula:
$σ$ is the population standard deviation
$x$ is an individual value
$μ$ is the average of the population
$N$ is the total number of the population
How to Find Standard Deviation (Population): Sample Problem
You have collected 10 rocks and measure the length of each in millimeters. Here’s your data:
$3, 5, 5, 6, 12, 10, 14, 4, 5, 8$
Let’s say you’re asked to calculate the population standard deviation of the length of the rocks.
Here are the steps to solve for that:
#1: Calculate the Mean of the Data
First, calculate the mean of the data. You’ll be finding the average of the data set.
$(3 + 5 + 5 + 6 + 12 + 10 + 14 + 4 + 13 + 8) = 80$
#2: Subtract the Average From Each Data Point, Then Square
Next, subtraction the average from each data point, then square the result.
Standard Deviation and Variance
Deviation just means how far from the normal
Standard Deviation
The Standard Deviation is a measure of how spread out numbers are.
Its symbol is Пѓ (the greek letter sigma)
The formula is easy: it is the square root of the Variance. So now you ask, «What is the Variance?»
Variance
The Variance is defined as:
The average of the squared differences from the Mean.
To calculate the variance follow these steps:
Example
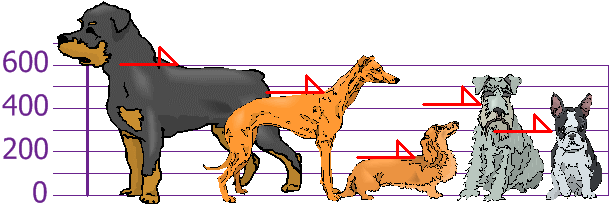
You and your friends have just measured the heights of your dogs (in millimeters):
The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
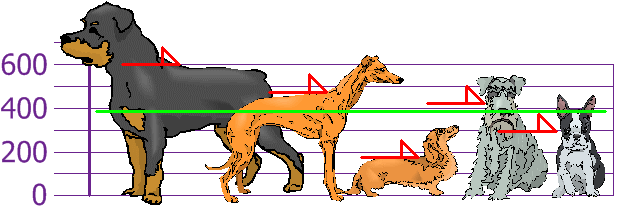
so the mean (average) height is 394 mm. Let’s plot this on the chart:
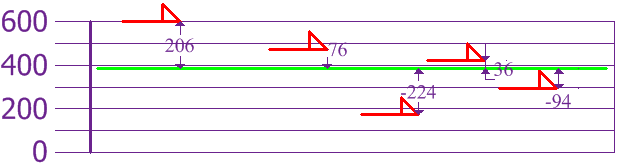
Now we calculate each dog’s difference from the Mean:
To calculate the Variance, take each difference, square it, and then average the result:
| Variance | ||
| Пѓ 2 | = | 206 2 + 76 2 + (в€’224) 2 + 36 2 + (в€’94) 2 5 |
| = | 42436 + 5776 + 50176 + 1296 + 88365 | |
| = | 1085205 | |
| = | 21704 | |
So the Variance is 21,704
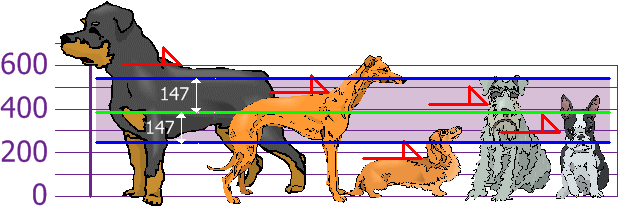
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| Пѓ | = | в€љ21704 |
| = | 147.32. | |
| = | 147 (to the nearest mm) | |
And the good thing about the Standard Deviation is that it is useful. Now we can show which heights are within one Standard Deviation (147mm) of the Mean:
So, using the Standard Deviation we have a «standard» way of knowing what is normal, and what is extra large or extra small.
Rottweilers are tall dogs. And Dachshunds are a bit short, right?
Using
We can expect about 68% of values to be within plus-or-minus 1 standard deviation.
Our example has been for a Population (the 5 dogs are the only dogs we are interested in).
But if the data is a Sample (a selection taken from a bigger Population), then the calculation changes!
When you have «N» data values that are:
All other calculations stay the same, including how we calculated the mean.
Example: if our 5 dogs are just a sample of a bigger population of dogs, we divide by 4 instead of 5 like this:
Think of it as a «correction» when your data is only a sample.
Formulas
Here are the two formulas, explained at Standard Deviation Formulas if you want to know more:
The «Population Standard Deviation»:


Looks complicated, but the important change is to
divide by N-1 (instead of N) when calculating a Sample Standard Deviation.
*Footnote: Why square the differences?
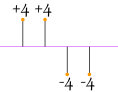 | 4 + 4 в€’ 4 в€’ 44 = 0 |
So that won’t work. How about we use absolute values?
 | |4| + |4| + |в€’4| + |в€’4|4 = 4 + 4 + 4 + 4 4 = 4 |
That looks good (and is the Mean Deviation), but what about this case:
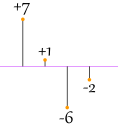 | |7| + |1| + |в€’6| + |в€’2|4 = 7 + 1 + 6 + 2 4 = 4 |
Oh No! It also gives a value of 4, Even though the differences are more spread out.
So let us try squaring each difference (and taking the square root at the end):
 | в€љ( 4 2 + 4 2 + (-4) 2 + (-4) 2 4 ) = в€љ( 64 4 ) = 4 |
 | в€љ( 7 2 + 1 2 + (-6) 2 + (-2) 2 4 ) = в€љ( 90 4 ) = 4.74. |
In fact this method is a similar idea to distance between points, just applied in a different way.
And it is easier to use algebra on squares and square roots than absolute values, which makes the standard deviation easy to use in other areas of mathematics.
Posted on 26th September 2018 by Eveliina Ilola
What is standard deviation?
Standard deviation tells you how spread out the data is. It is a measure of how far each observed value is from the mean. In any distribution, about 95% of values will be within 2 standard deviations of the mean.
How to calculate standard deviation
Standard deviation is rarely calculated by hand. It can, however, be done using the formula below, where x represents a value in a data set, μ represents the mean of the data set and N represents the number of values in the data set.
The steps in calculating the standard deviation are as follows:
What is standard error?
When you are conducting research, you often only collect data of a small sample of the whole population. Because of this, you are likely to end up with slightly different sets of values with slightly different means each time.
If you take enough samples from a population, the means will be arranged into a distribution around the true population mean. The standard deviation of this distribution, i.e. the standard deviation of sample means, is called the standard error.
The standard error tells you how accurate the mean of any given sample from that population is likely to be compared to the true population mean. When the standard error increases, i.e. the means are more spread out, it becomes more likely that any given mean is an inaccurate representation of the true population mean.
How to calculate standard error
Standard error can be calculated using the formula below, where σ represents standard deviation and n represents sample size.
How to Calculate Standard Deviation 2
Standard deviation is a measurement of how spread out the numbers are of a set of data values. The closer the standard deviation is to zero, the closer the data points are to the mean. Large values of standard deviation indicate the data spreads out away from the mean. Here is how to calculate the standard deviation of a set of data.
Population Standard Deviation
Standard deviation, represented by the lower case Greek letter, σ is calculated from the variance from the mean of each data point. Variance is simply the average of the squared difference of each data point from the mean.
There are three steps to calculating variance:
Example: Let’s take a set of test scores from a math class of nine students. The scores were:
65, 95, 73, 88, 83, 92, 74, 83, and 94
Step 1 is find the mean. To find the mean, add all these scores together.
65 + 95 + 73 + 88 + 83 + 92 + 74 + 83 + 94 = 747
Divide this value by the total number of tests (9 scores)
The mean score on the test was a score of 83.
For step 2, we need to subtract the mean from each test score and square each result.
(65 – 83)² = (-18)² = 324
(95 – 83)² = (12)² =144
(73 – 83)² = (-10)² = 100
(88 – 83)² = (5)² = 25
(83 – 83)² = (0)² = 0
(92 – 83)² = (9)² = 81
(74 – 83)² = (-9)² = 81
(83 – 83)² = (0)² = 0
(94 – 83)² = (11)² = 121
Step 3 is find the mean of these values. Add them all together:
324 + 144 + 100 + 25 + 0 + 81 + 81 + 0 + 121 = 876
Divide this value by the total number of scores (9 scores)
876 ÷ 9 = 97 (rounded to the nearest whole score)
The variance of the test scores is 97.
The standard deviation is simply the square root of the variance.
σ = √97 = 9.8 (round to nearest whole test score = 10)
This means scores within one standard deviation, or 10 points of the average score could be all considered ‘average scores’ of the class. The two scores 65 and 73 would be considered ‘below average’ and the 94 would be ‘above average’.
This calculation of standard deviation is for population measurements. This is when you can account for all the data in the population of the set. This example had a class of nine students. We know all the scores of all the students in the class. What if these nine scores were randomly taken from a larger set of scores, say the entire 8th Grade. The set of nine test scores is considered a sample set from the population.
How to Calculate Sample Standard Deviation
Sample standard deviations are calculated slightly different. The first two steps are identical. In step 3, instead of dividing by the total number of tests, you divide by one less than the total number.
In our example above, the total from step 2 added together was 876 for 9 test scores. To find the sample variance, divide this number by one less than 9, or 8
The sample variance is 109.5. Take the square root of this value to get the sample standard deviation:
sample standard deviation = √109.5 = 10.5
Review
To find the population standard deviation:
To find the sample standard deviation:
Related Posts
2 thoughts on “ How to Calculate Standard Deviation ”
The devil is in the details.
Thank you for pointing out the error. Updated and fixed.
The outlying data should be retained. Researchers look for explanations for reasons why data didn’t fit the curve, but shouldn’t discount it. Sometimes it’s random chance, but sometimes there is a new discovery to be made there 🙂
How to Find the Standard Deviation of a Probability Distribution
A probability distribution tells us the probability that a random variable takes on certain values.
For example, the following probability distribution tells us the probability that a certain soccer team scores a certain number of goals in a given game:
To find the standard deviation of a probability distribution, we can use the following formula:
For example, consider our probability distribution for the soccer team:
The mean number of goals for the soccer team would be calculated as:
μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 goals.
We could then calculate the standard deviation as:
The standard deviation is the square root of the sum of the values in the third column. Thus, we would calculate it as:
The variance is simply the standard deviation squared, so:
The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios.
Example 1: Standard Deviation of Vehicle Failures
The following probability distribution tells us the probability that a given vehicle experiences a certain number of battery failures during a 10-year span:
Question: What is the standard deviation of the number of failures for this vehicle?
Solution: The mean number of expected failures is calculated as:
μ = 0*0.24 + 1*0.57 + 2*0.16 + 3*0.03 = 0.98 failures.
We could then calculate the standard deviation as:
The standard deviation is the square root of the sum of the values in the third column. Thus, we would calculate it as:
Example 2: Standard Deviation of Sales
The following probability distribution tells us the probability that a given salesman will make a certain number of sales in the upcoming month:
Question: What is the standard deviation of the number of sales for this salesman in the upcoming month?
Solution: The mean number of expected sales is calculated as:
μ = 10*.24 + 20*.31 + 30*0.39 + 40*0.06 = 22.7 sales.
We could then calculate the standard deviation as:
The standard deviation is the square root of the sum of the values in the third column. Thus, we would calculate it as:
Standard deviation = √ (38.7096 + 2.2599 + 20.7831 + 17.9574) = 8.928