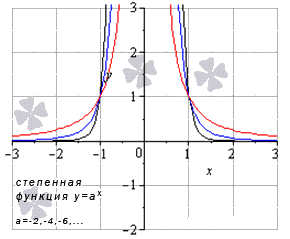
К чему стремится косинус при х 0

Непосредственное вычисление пределов, таблица пределов функций

Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.

Значение предела в точке непрерывности определено значением функции в этой точке.

При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.

Произвести вычисление предела функции lim x → 5 a r c t g 3 5 · x

Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x 0 = 5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что

lim x → 5 a r c t g 3 5 · x = a r c t g 3 5 · 5 = a r c t g 3 = π 3

Для упрощения выражений применяют свойства пределов:

Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.

Таблица пределов функции

Для упрощения и решения пределов используется данная таблица основных пределов.

Функция корень n-ой степени

Для любых x 0 из опрелеления

lim x → x 0 x n = x 0 n

Функция корень n-ой степени

lim x → x 0 x n = x 0 n

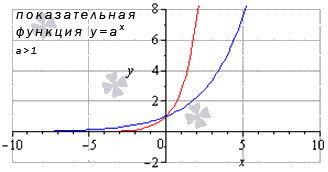
Показательная функия

Для любых x 0 из области опреления lim x → x 0 a x = a x 0

Показательная функия

Для любых знвчений x 0 из област опредения lim x → x 0 a x = a x 0

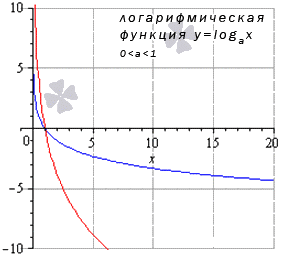
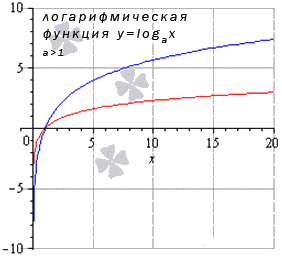
Логарифмическая функция

Для любых x 0 из области опрелеления lim x → x 0 log a x = log a x 0

Логарифмическая функция

Для любых x 0 из области опрелеления

lim x → x 0 log a x = log a x 0

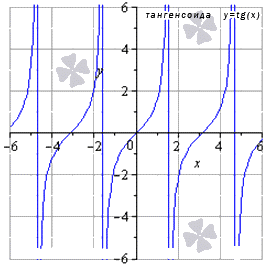
lim x → ∞ t g x не существует

Для любых x 0 из области опрелеления

lim x → x 0 t g x = t g x 0

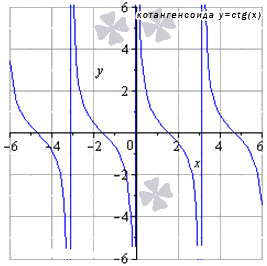
lim x → ∞ c t g x не существует

Для любых x 0 из области опрелеления
lim x → x 0 с t g x = с t g x 0

Обратные тригонометрические функции

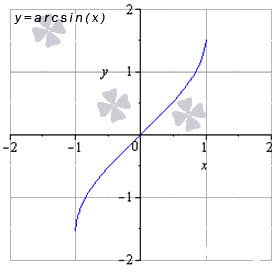
Для любых x 0 из области опрелеления

lim x → x 0 a r c sin x = a r c sin x 0

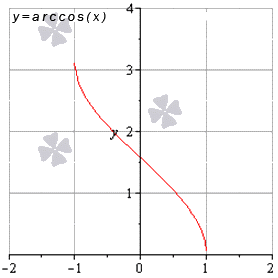
Для любых x 0 из области опрелеления

lim x → x 0 a r c c i s x = a r c cos x 0

Обратные тригонометрические функции

Для любых x 0 из области опрелеления

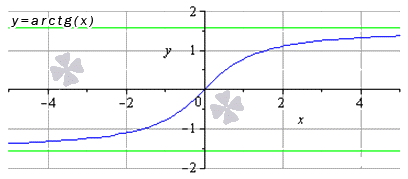
lim x → x 0 a r c t g x = a r c t g x 0

Для любых x 0 из области опрелеления

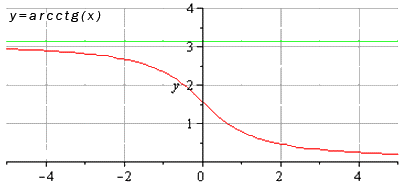
lim x → x 0 a r c c t g x = a r c c t g x 0

По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что

Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.

Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.

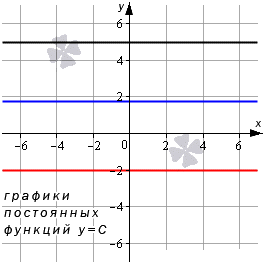
Предел константы

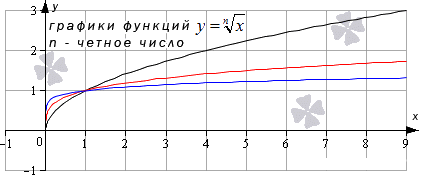
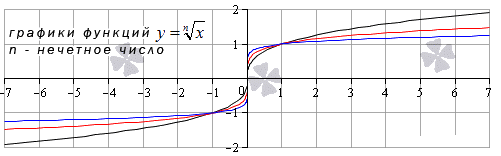
Предел функции корень n-ой степени

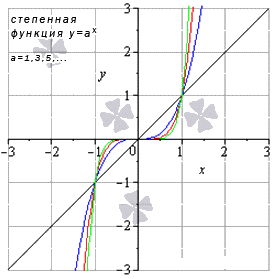
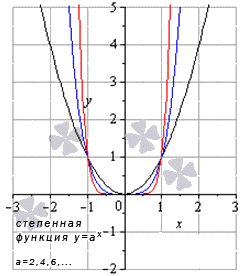
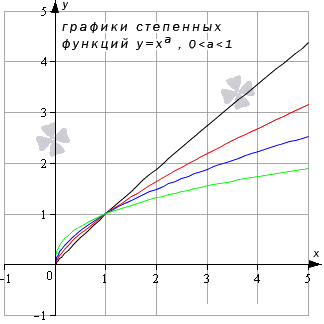
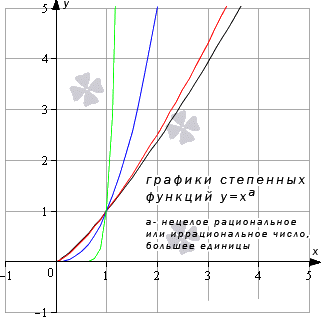
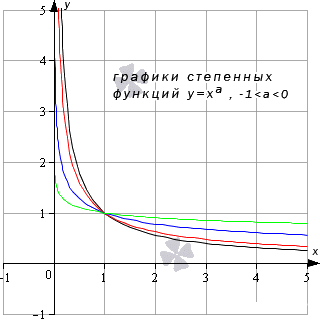
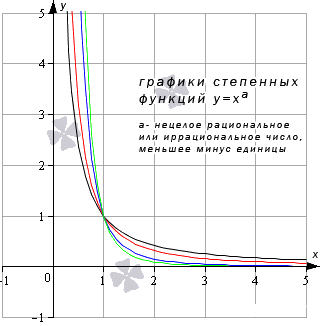
Предел степенной функции

Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.

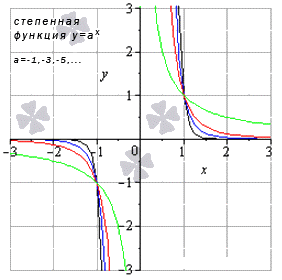
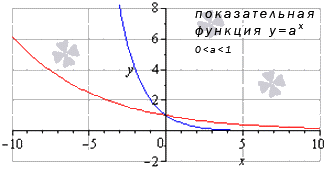
Предел показательной функции

Предел логарифмической функции

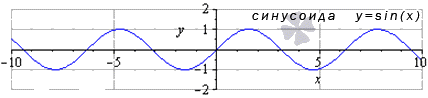
Предел тригонометрических функций

Предел обратных тригонометрических функций

Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

К чему стремится косинус при х 0

ФУНКЦИИ И ПРЕДЕЛЫ IX

§ 213. Некоторые тригонометрические неравенства
и их использование при нахождении пределов

В этом параграфе мы докажем некоторые тригонометрические неравенства, которые будут играть важную роль в дальнейшем изучении функций.

1. Для любого острого угла х (выраженного в радианах)

S_{сект. OAB} = ;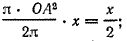

Учитывая, что BD = sin х, АС = tg x, получаем:

откуда и вытекает неравенство (1).

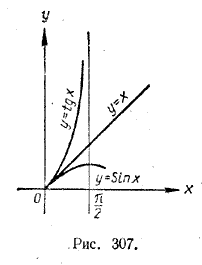
Рисунок 307 служит графической иллюстрацией неравенства (1).

В интервале (0, π /₂) график функции у = х расположен выше графика функции у = sin х, но н и ж е графика функции у = tg x.

Остановимся подробнее на неравенстве sin x π /₂. Но при таком предположении х и sin x положительны. Поэтому х = |х| и sin х = |sin х| и неравенство sin х π /₂, 0), так как

Перепишем неравенство (2) в виде:

(Поскольку 0 = sin 0, то полученный результат по существу означает, что функция у = sin x непрерывна в нуле (то есть при х = 0.)

2. Для любого острого угла х (выраженного в радианах)

что и доказывает формулу (3).

Поскольку 1 = cos 0, то полученный результат по существу означает, что функция у = cos х непрерывна в нуле.

Отсюда, используя доказанную выше непрерывность в нуле функции у = sin х, легко показать, что функции у = sin х и у = cos x непрерывны в любой точке х. Попробуйте это сделать сами!

Найти пределы (№ 1676 —1681):

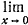
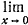
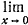
1676. tg х. 1678. sin ( π /₄ + х). 1680. tg ( π /₃ +2х).

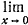
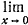
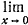
1677. cos x /₂. 1679. sin 2х. 1681. cos ( π /₃ — х ).

1682. Доказать тождества:

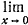
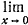
a) sin (х + α) = sin α; 6) cos (х + α) = cos α.

1683. Для всех ли положительных значений х верны неравенства:

1684. Докажите, что единственным корнем уравнения sin х = х является х = 0.

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник