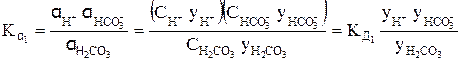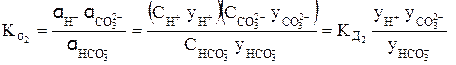Коэффициент активности тем больше чем
Активность и коэффициент активности. Ионная сила раствора
Неподчинение растворов сильных электролитов закону действия масс, а также законам Рауля и Вант-Гоффа объясняется тем, что эти законы применяются к идеальным газовым и жидким системам. При выводе и формулировке этих законов не учитывались силовые поля частиц. В 1907 г. Льюис предложил внести в науку понятие «активность».
Активность (α) учитывает взаимное притяжение ионов, взаимодействие растворенного вещества с растворителем, присутствие других электролитов и явления, изменяющие подвижность ионов в растворе. Активностью называется эффективная (кажущаяся) концентрация вещества (иона), соответственно которой ионы проявляют себя в химических процессах в качестве реальной действующей массы. Активность для бесконечно разбавленных растворов равна молярной концентрации вещества: α = с и выражается в грамм ионах на литр.
а активность равна молярной концентрации, умноженной на коэффициент активности: α = cf.
Для сильных электролитов молярную концентрацию ионов (с) вычисляют, исходя из допущения полной диссоциации их в растворе. Физико-химики различают активную и аналитическую концентрацию ионов в растворе. Активной концентрацией называется концентрация свободных гидратированных ионов в растворе, а аналитической концентрацией — общая молярная концентрация ионов, определяемая, например, путем титрования.
Коэффициент активности ионов зависит не только от концентрации ионов данного электролита, но и от концентрации всех посторонних ионов, присутствующих в растворе. Величина коэффициента активности понижается с возрастанием ионной силы раствора.
Ионной силой раствора (m,) называется величина электрического поля в растворе, являющаяся мерой электростатического взаимодействия между всеми ионами в растворе. Она вычисляется по формуле, предложенной Г. Н. Льюисом и М. Ренделом в 1921 г.:
где c1, c2 и cn — молярные концентрации отдельных ионов, присутствующие в растворе, a Z 2 1, Z2 2 и Z 2 n — их заряды, взятые в квадрате. Недиссоциированные молекулы, как не имеющие зарядов, в формулу подсчета ионной силы раствора не включаются.
Таким обраэом, ионная сила раствора равна полусумме произведений концентраций ионов на квадраты их зарядов, что можно выразить уравнением: µ = 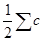
Рассмотрим несколько примеров.
Пример 1.Вычислить ионную силу 0,01 М раствора хлорида калия КС1.
| m = | (0,01 · 1 2 + 0,01 · 1 2 ) = 0,01 |
т. е. ионная сила разбавленного раствора бинарного электролита типа KtAn равна молярной концентрации электролита: m = с.
Пример 2. Вычислить ионную силу 0,005 М раствора нитрата бария Ва(NO3)2.
| m = | (0,005 · 2 2 + 0,01· 1 2 ) = 0,015 |
Ионная сила разбавленного раствора электролита типа KtAn2 и Kt2An равна: m = 3с.
Пример 3. Вычислить ионную силу 0,002 М раствора сульфата цинка ZnSO4.
| m = | (0,002 · 2 2 + 0,002 · 2 2 ) = 0,008 |
Отсюда, ионная сила раствора электролита типа Kt 2+ An 2- равна:m = 4с.
Если в растворе присутствует два или несколько электролитов, то вычисляется общая ионная сила раствора.
Примечание. В справочниках по химии даются дифференцированные коэффициенты активности отдельных ионов или же для групп ионов. (См.: Лурье Ю. Ю. Справочник по аналитической химии. М., 1971.)
С увеличением концентрации раствора при полной диссоциации молекул электролита количество ионов в растворе значительно »возрастает, что приводит к увеличению ионной силы раствора и значительному уменьшению коэффициентов активности ионов. Г. Н. Льюис и М. Рендель нашли закон ионной силы, согласно которому коэффициенты активности ионов одной и той же зарядности одинаковые во всех разбавленных растворах, имеющих одинаковую ионную силу. Однако этот закон применим лишь к очень разбавленным водным растворам, с ионной силой до 0,02 г-ион/л. При дальнейшем повышении концентрации, а следовательно, и ионной силы раствора начинаются отступления от закона ионной силы, вызываемые природой электролита (табл. 2.2).
Таблица 2.2 Приближенные значения коэффициентов активности при разной ионной силе
В настоящее время для аналитических вычислении пользуются таблицей приближенных значений коэффициентов активности.
Зависимость коэффициентов активности ионов от ионной силы раствора для очень разбавленных растворов электролитов вычисляется по приближенной формуле Дебая — Хюккеля:
где А — множитель, величина которого зависит от температуры (при 15°С, А = 0,5).
При значениях ионной силы раствора до 0,005 величина 1 + 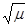
приобретает более простой вид:
В качественном анализе, где приходится иметь дело со сложными смесями электролитов и где часто не требуется большой точности, при вычислении активностей ионов можно пользоваться таблицей 2.2.
Пример 4. Вычислить активность ионов в растворе, содержащем в 1 л 0,001 моль сульфата калия-алюминия.
1. Вычислим ионную силу раствора:
| m = | ([K + ]·1 2 +[Al 3+ ]·3 2 )+2[SO 2- 4] ·2 2 ) = | ( 0,001 ·1+0,001·9+2 ·0,001 ·4)= |
2. Находим приближенное значение коэффициентов активности данных ионов. Так, в рассматриваемом примере ионная сила равна 0,009. Наиболее близкой к ней ионной силой, указанной в таблице 2.2, является 0,01. Следовательно, без большой погрешности можно взять для ионов калия fK+ = 0,90; для ионов алюминия fAl 3+ = 0,44, а для сульфат-ионов fSO 2- 4 = 0,67.
3. Вычислим активность ионов:
Решение примера 4 с использованием метода интерполяции.
1. Находим коэффициент активности ионов калия fK+.
При ионной силе раствора, равной 0,005, fK+ равен 0,925, а при ионной силе раствора, равной 0,01, fK+, равен 0,900. Следовательно, разности ионной силы раствора m, равной 0,005, соответствует разность fK+, равная 0,025 (0,925—0,900), а разности ионной силы m, равной 0,004 (0,009 — 0,005), соответствует разность fK+, равная х.
Отсюда, х = 0,020. Следовательно, fK+ = 0,925 — 0,020 = 0,905
откуда х = 0,07·0,004/ 0,005 = 0,056
Так же находим коэффициент активности сульфат-ионов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Коэффициент активности
СОДЕРЖАНИЕ
Термодинамическое определение [ править ]
μ B знак равно μ B ⊖ + р Т пер Икс B <\ displaystyle \ mu _ <\ mathrm > = \ mu _ <\ mathrm > ^ <\ ominus>+ RT \ ln x _ <\ mathrm > \,>
Это обобщается, чтобы включить неидеальное поведение, написав
μ B знак равно μ B ⊖ + р Т пер а B <\ displaystyle \ mu _ <\ mathrm > = \ mu _ <\ mathrm > ^ <\ ominus>+ RT \ ln a _ <\ mathrm > \,>
когда В это активность вещества в смеси с
а B знак равно Икс B γ B <\ displaystyle a _ <\ mathrm > = x _ <\ mathrm > \ gamma _ <\ mathrm >>
Подробно: закон Рауля гласит, что парциальное давление компонента B связано с его давлением пара (давлением насыщения) и его мольной долей x B в жидкой фазе,
Другими словами: соединение показывает неидеальное поведение в разбавленном случае.
Приведенное выше определение коэффициента активности нецелесообразно, если соединение не существует в виде чистой жидкости. Это часто бывает с электролитами или биохимическими соединениями. В таких случаях используется другое определение, в котором бесконечное разбавление рассматривается как идеальное состояние:
Здесь символ используется для различения двух видов коэффициентов активности. Обычно его опускают, так как из контекста ясно, какой вид имеется в виду. Но есть случаи, когда требуются оба вида коэффициентов активности, которые могут даже входить в одно и то же уравнение, например, для растворов солей в смесях (вода + спирт). Иногда это является источником ошибок. † <\displaystyle ^<\dagger >>
Изменение мольных долей или концентраций с помощью коэффициентов активности дает эффективные активности компонентов и, следовательно, позволяет применять такие выражения, как закон Рауля и константы равновесия, как к идеальным, так и к неидеальным смесям.
Ионные растворы [ править ]
Для электролита 1: 1, такого как NaCl, он определяется следующим образом:
где γ + и γ — коэффициенты активности катиона и аниона соответственно.
В более общем смысле, средний коэффициент активности соединения формулы A p B q определяется как [4]
γ ± = γ A p γ B q p + q <\displaystyle \gamma _<\pm >=<\sqrt[
\gamma _ <\mathrm >^>>>
Преобладающее мнение о том, что коэффициенты активности отдельных ионов невозможно измерить независимо или, возможно, даже физически бессмысленно, уходит своими корнями в работы Гуггенхайма в конце 1920-х годов. [5] Однако химики никогда не могли отказаться от идеи активности одного иона и, как следствие, коэффициентов активности одного иона. Например, pH определяется как отрицательный логарифм активности ионов водорода. Если преобладающая точка зрения на физический смысл и измеримость активности одного иона верна, то определение pH как отрицательного логарифма активности ионов водорода помещает эту величину в категорию неизмеримых. Признавая эту логическую трудность, Международный союз теоретической и прикладной химии(IUPAC) утверждает, что определение pH на основе активности является только условным определением. [6] Несмотря на преобладающее отрицательное мнение об измеримости одноионных коэффициентов, концепция активности отдельных ионов продолжает обсуждаться в литературе, и, по крайней мере, один автор представляет определение активности одного иона в терминах чисто термодинамических величин и предлагает метод измерения коэффициентов активности одиночных ионов, основанный на чисто термодинамических процессах. [7]
Концентрированные ионные растворы [ править ]
Для концентрированных ионных растворов необходимо учитывать гидратацию ионов, как это было сделано Стоксом и Робинсоном в их модели гидратации от 1948 года. [8] Коэффициент активности электролита разделен на электрические и статистические компоненты Э. Глюкауфом, который модифицирует Модель Робинсона – Стокса.
Статистическая часть коэффициента активности концентрированного раствора составляет:
ln γ s = h − ν ν ln ( 1 + b r 55.5 ) − h ν ln ( 1 − b r 55.5 ) + b r ( r + h − ν ) 55.5 ( 1 + b r 55.5 ) <\displaystyle \ln \gamma _=<\frac
<55.5>>\right)-<\frac
<55.5>>\right)+<\frac
<55.5>>\right)>>> 
Модель Стокса – Робинсона анализировалась и улучшалась также другими исследователями. [12] [13]
Экспериментальное определение коэффициентов активности [ править ]
Радиохимические методы [ править ]
Коэффициенты активности можно определить радиохимическими методами. [14]
При бесконечном разбавлении [ править ]
Коэффициенты активности для бинарных смесей часто указываются при бесконечном разбавлении каждого компонента. Поскольку модели коэффициента активности упрощаются при бесконечном разбавлении, такие эмпирические значения могут использоваться для оценки энергий взаимодействия. Приведены примеры для воды:
| Икс | γ x ∞ (К) | γ W ∞ (К) |
|---|---|---|
| Этанол | 4,3800 (283,15) | 3,2800 (298,15) |
| Ацетон | 6,0200 (307,85) |
Теоретический расчет коэффициентов активности [ править ]
Для незаряженных видов коэффициент активности γ 0 в основном соответствует модели высаливания : [24]
log 10 ( γ 0 ) = b I <\displaystyle \log _<10>(\gamma _<0>)=bI>
Для воды в качестве растворителя активность a w можно рассчитать по формуле [24]
Ссылка на ионный диаметр [ править ]
log ( γ i ) = − A z i 2 I 1 + B a I <\displaystyle \log(\gamma _)=-<\frac
Зависимость от параметров состояния [ править ]
Производная коэффициента активности по температуре связана с избыточной молярной энтальпией соотношением
H ¯ i E = − R T 2 ∂ ∂ T ln ( γ i ) <\displaystyle <\bar
Точно так же производная коэффициента активности по давлению может быть связана с избыточным молярным объемом.
V ¯ i E = R T ∂ ∂ P ln ( γ i ) <\displaystyle <\bar
Приложение к химическому равновесию [ править ]
В состоянии равновесия сумма химических потенциалов реагентов равна сумме химических потенциалов продуктов. Изменение свободной энергии Гиббса для реакций Δ r G равно разности этих сумм и, следовательно, в состоянии равновесия равно нулю. Таким образом, для такого равновесия, как
Подставьте в выражения для химического потенциала каждого реагента:
После перестановки это выражение становится
Δ r G ⊖ = − R T ln K <\displaystyle \Delta _
Этот вывод служит двум целям. Он показывает взаимосвязь между стандартным изменением свободной энергии и константой равновесия. Это также показывает, что константа равновесия определяется как отношение активности. На практике это неудобно. Когда каждое действие заменяется произведением концентрации на коэффициент активности, константа равновесия определяется как
где [S] обозначает концентрацию S и т. д. На практике константы равновесия определяются в среде таким образом, чтобы коэффициент коэффициента активности был постоянным и им можно было пренебречь, что приводит к обычному выражению
который применяется при условиях, когда коэффициент активности имеет определенное (постоянное) значение.
Дополнения. 1. Активность. Коэффициент активности



1. Активность. Коэффициент активности.
Ионная сила раствора. Термодинамическая константа диссоциации
В водных растворах электролитов наличие зарядов у ионов электростатически тормозит передвижение их. Поэтому концентрация растворённого вещества без учёта сил взаимодействия между ионами и молекулами в растворе не может полностью характеризовать свойства его. Чем выше концентрация раствора, содержащего многозарядные ионы, тем значительнее в нём силы взаимодействия между ионами и тем больше отклонения от закона действующих масс.
Способность ионов к химическим реакциям, вызываемая их электростатическим взаимодействием, характеризуется активностью.
Активность ионов связана с концентрацией вещества в растворе уравнением
где α – активность ионов выражает эффективную концентрацию электролита в растворе (иначе «термодинамическую концентрацию»), имеет ту же единицу измерения, что и концентрация; g – моляльный коэффициент активности учитывает все те силы, которые действуют в растворе, и в первую очередь, силы электростатического взаимодействия между ионами. Коэффициент активности безразмерная величина. Он характеризует работу перенесения одного моля растворенного вещества из идеального в реальный раствор при Р, Т = const; Cm – моляльность вещества В в растворе, моль/1000 г Н2О или моль/кг Н2О.
В том случае, если раствор имеет молярную концентрацию вещества В, то уравнение (1) примет вид
где у – молярный коэффициент активности; С – молярная концентрация вещества В, моль/л.
Активность вещества АmВn, диссоциирующего в водном растворе по уравнению
равна 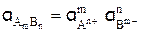
Для разбавленных растворов слабых электролитов коэффициент активности у = 1 и α = С. Поэтому слабые электролиты подчиняются с достаточной точностью закону действующих масс, и при проведении расчётов в формулу закона действующих масс можно подставлять концентрации ионов.
Для концентрированных растворов слабых кислот следует пользоваться значениями активности ионов, а не концентрациями.
Так, для концентрированного раствора слабой угольной кислоты, в отличие от разбавленного раствора, выражения для константы диссоциации этой кислоты по первой и второй ступеням в растворах, имеющих молярную концентрацию, будет иметь вид:
H2CO3 « H + + 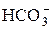
или 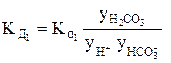
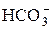
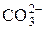
или 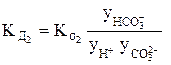
В выражениях (4) и (5) 
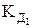
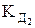
Согласно уравнениям (4) и (5) при уменьшении концентрации ионов в растворе кислоты у ® 1, а Кα приближается к Кд.
Для сильных электролитов g » у » l только в очень разбавленных растворах
(С –4 моль/л) и α » С. При С > 10 –4 моль/л коэффициент активности, как правило, меньше единицы. Это значит, что ион стеснён в своих движениях межионными силами, и α
Вычисления величин коэффициентов активности очень сложны. Но для разбавленных растворов коэффициент активности может быть рассчитан по формулам:
lgg = –0,5 Zк Zа 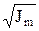
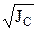
где g и у – средний моляльный и молярный коэффициенты активности;
Zк и Zа – заряд катиона и аниона; Jm и Jc – ионные силы раствора для моляльной и молярной концентраций соответственно.
Ионная сила раствора является мерой напряжённости электрического поля, существующего в растворе, и равна полусумме произведении концентраций всех ионов, присутствующих в растворе на квадрат их заряда:
Jm = 0,5 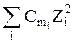
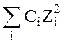
где Cm и С – моляльная и молярная концентрации соответственно; Zi – заряд иона.
Ионная сила Jm имеет единицу моль/1000 г Н2О или моль/кг Н2О, Jc – моль/л.
В разбавленных растворах электролитов с одинаковой ионной силой коэффициенты активности большинства ионов, имеющих один и тот же заряд, приблизительно одинаковы (см. табл. 1).
Пример 1. Найдите коэффициенты активности ионов Fe 3+ и 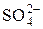
Пользуясь табл. 1, находим, что при Jc = 0,0001 (10 –4 ) моль/л, коэффициент активности иона Fe 3+ равен 0,9, а иона 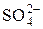
Приближённые значения средних коэффициентов активности
ионов в зависимости от ионной силы раствора
| Ионная сила JС, моль/л | Коэффициент активности у | |||
| Однозарядные ионы | Двухзарядные ионы | Трёхзарядные ионы | Четырёхзарядные ионы | |
| 1×10 –4 | 0,99 | 0,95 | 0,90 | 0,83 |
| 1×10 –3 | 0,96 | 0,86 | 0,73 | 0,56 |
| 1×10 –2 | 0,89 | 0,63 | 0,39 | 0,19 |
| 1×10 –1 | 0,78 | 0,33 | 0,08 | 0,01 |
Пример 2. Найдите активность ионов Na + и Сl – в 0,001 М растворе NaCl. Ионная сила 0,001 М раствора NaCl (см. уравнение 7) равна
Jc = 0,5( 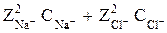
Средний коэффициент активности у при ионной силе раствора 10 –3 моль/л для однозарядных ионов равен 0,96 (см. табл. 11). Следовательно, активность ионов
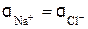
Пример 3. Найдите активность 0,005 М раствора Al2(SО4)3, если 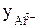
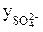
Активность раствора Al2(SО4)3 (см, уравнение 3) равна
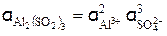
Пример 4. Найдите ионную силу раствора, содержащего 0,04 моль Рb(NO3)2 и 0,02 моль К2SO4 в 2 л раствора.
Находим содержание количества вещества (моль) Рb(NO3)2 и К2SO4 в 1 л раствора. Это будет 0,02 моль Рb(NO3)2 и 0,01 моль К2SO4. Ионная сила раствора (см. уравнение 7)
Jc = 0,5( 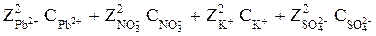
= 0,5(2 2 ×0,02 + 1 2 ×0,02 + 1 2 ×0,01 + 2 2 ×0,01) = 0,09 моль/л.