Корреляция это что прямая
Корреляция: это простыми словами
Что представляет собой корреляция?
Термин «корреляция» пугает многих людей и кажется чем-то сложным и непонятным. Однако на практике ничего устрашающего в ней нет. Корреляция – это всего лишь показатель, показывающий зависимость между событиями или объектами.
Данное понятие применяется в экономическом и статистическом анализе, психологии, биологии, математике. Например, если посмотреть на небо и увидеть густые и темные тучи, то можно прийти к выводу, что скоро пойдет дождь. Однако наше умозаключение не дает 100% гарантии. Это и является отличительной особенностью корреляцию от линейной зависимости.
Что такое корреляция?
Корреляция – это взаимозависимость случайных факторов. Она отображает приближенную взаимосвязь и не дает точных ответов. Например, в стране выросла безработица и увеличилось количество преступлений. Можно предположить, что на второй фактор повлияли первый. Но на уровень преступности также влияют воспитание, менталитет людей, уровень образования. Составить точный прогноз нереально, так как всегда есть дополнительные факторы.
Связь может быть трех видов:
Например, повышения уровня радиации негативно сказывается на здоровье человека. Межу событиями имеется обратно пропорциональная зависимость – увеличения радиации приводит к ухудшению здоровья. Коэффициент корреляции при этом имеет отрицательное значение.
Некоторые события или явления практически никак не связаны друг с другом. Утром у вас разрядился телефон, а вчера в маршрутке вам на ногу наступил мужчина. Ни одно из событий не влияет на другое. В данном случае коэффициент корреляции равен нулю.
Если коэффициент больше нуля и стремится к 1, то такая корреляция называется положительной. Она показывает прямую взаимосвязь между событиями. Например, чем выше уровень знаний, тем выше шансы поступить в университет на бюджет.
Анализ корреляционного соотношения помогает выдвинуть гипотезу о причинно-следственных связях.
Корреляция цены на нефть и курса доллара
Цена на нефть и курс американского доллара имеют обратную корреляционную связь. При росте стоимости «черного золота» курс доллара снижается и наоборот.
США обладают самой мощной промышленностью в мире и на ее нужды требуется просто огромное количество нефти. В то же время Штаты входят в первую десятку стран по уровню добычи этого природного ресурса. При этом США значительную часть добытой нефти экспортируют, что вызывает дефицит в промышленности. Для его покрытия американцы ежегодно импортируют свыше 8 миллиардов баррелей нефти.
Данного объема достаточно для влияния на курс национальной валюты. Увеличение спроса США на нефть приводит к увеличению цены на международном рынке. В свою очередь, рост объемов импорта влияет на стоимость произведенных товаров. В итоге на валютном рынке наблюдается избыток американской валюты, и ее курс начинает падать.
Корреляция в управлении инвестиционными активами
Корреляция активно используется инвесторами при формировании и управлении своих инвестиционных портфелях. Логично, что нельзя держать все свои активы в одном месте. Диверсификация позволяет значительно снизить риски.
Например, инвестор покупает акции одной крупной компании и нескольких мелких. Коэффициент корреляции акций гигантов отрасли и небольших предприятий приблизительно равен +0,8. Это достаточно большое значение и оно характеризует прямую зависимость между объектами. При падении акции крупной компании существует большая вероятность, что стоимость ценных бумаг небольших фирм тоже снизится существенная. В данном случае лучше подбирать активы таким образом, что корреляционные связи были минимальными.
Для этого, например, инвестор может составить свой портфель из акций и облигаций или акций и казначейских векселей. Облигации между собой, как и акции, также имеют прямую связь. Их коэффициент еще выше. Однако между облигациями и акциями такой зависимости нет, что и позволяет инвестору снизить риски.
Также наблюдается зависимость между странами и даже регионами. Чем ближе они находятся, тем выше коэффициент корреляции. Например, для Канады и США он составляет 0,9. В то же время для Японии и США он на 4 десятых меньше. Собственно, инвестору более выгодно покупать активы эмитентов из разных регионов.
Золото и ценные бумаги практически не коррелируются. Однако серебро и золото очень зависимы друг от друга, так же, как и евро и американский доллар. Их использование в рамках одного инвестиционного портфеля нецелесообразно.
Корреляция – это удобный и необходимый инструмент в различных сферах жизни. Она не является панацеей, но позволяет достаточно точно установить причинно-следственные связи между явлениями.
Что такое корреляция акций и облигаций?
Объясните, пожалуйста, простым языком, что такое корреляция ценных бумаг? Почему о ней говорят при составлении портфеля и что значит, когда она отрицательная?
Корреляция показывает, насколько активы схожи по поведению. Показатель описывает закономерности. Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция. Это относится как к отдельным ценным бумагам, так и к широким рынкам, классам активов и секторам экономики.
Коэффициент корреляции вычисляется на конкретном историческом отрезке. Он обозначается буквой r и принимает значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях — ближе к −1. Но когда корреляция близка к нулю, взаимосвязи между ними нет. Это значит, что при росте или падении одного актива другой может вообще никак себя не проявлять. Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год составила 0,11.
Расскажу, как можно использовать знание о корреляции при формировании портфеля.
Роль корреляции в управлении портфелем
Понимание корреляции между инструментами позволяет диверсифицировать портфель и снизить инвестиционные риски.
Например, если инвестор собрал портфель из 10 нефтегазовых компаний, он защитил себя только от специфических рисков, связанных с конкретным эмитентом. Волатильность портфеля по-прежнему будет высокой: если цены на нефть упадут, портфель также уйдет в красную зону из-за тесной корреляции акций.
Чтобы диверсификация работала, необходимо использовать инструменты с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. Так, государственные облигации — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.
Таким же образом устроен и механизм хеджирования, когда инвестор открывает позицию с отрицательной корреляцией к исходному активу, чтобы застраховаться от его падения. Например, так называемые обратные ETF обладают корреляцией, близкой к −1 по отношению к исходному активу.
Как победить выгорание
Как изменяется корреляция со временем
Современная теория портфеля позволяет найти идеальную смесь активов, при которой у портфеля будет оптимальное соотношение доходности и риска. Но главный недостаток этой теории в том, что корреляции со временем могут меняться. Два актива могут начать двигаться синхронно, даже если в прошлом их взаимосвязь была низкой. И заметить это можно только постфактум — на исторических данных.
Например, компания Blackstone провела исследование корреляции между разными классами активов за 20 лет. Результаты показали, что корреляция со временем только увеличивается. Это связано с разными факторами: тесной интеграцией экономик, глобальными производственными цепочками и усилившимся влиянием рынков друг на друга.
Seeking an Alternative — BlackstonePDF, 421 КБ
Если посмотреть на десятилетие перед кризисом 2008 года, то корреляция большинства инструментов по отношению к S&P 500 была ниже 0,5. Но после 2008 года она заметно выросла. Теперь только у высоконадежных облигаций по-прежнему слабая связь с акциями, хотя их корреляция сменилась с отрицательной на положительную: если раньше при падении S&P 500 они росли, то теперь тоже падают, пусть и не так сильно.
Корреляция различных классов активов с индексом S&P 500
| 1998—2007 | 2008—2020 | |
|---|---|---|
| Глобальные акции | 0,84 | 0,89 |
| Недвижимость | 0,32 | 0,74 |
| Высокодоходные облигации | 0,49 | 0,73 |
| Товары | −0,01 | 0,59 |
| Высоконадежные облигации | −0,21 | 0,01 |
Корреляция и волатильность
Между корреляцией и волатильностью существует взаимосвязь: когда рынки становятся волатильными, корреляции между инструментами возрастают. Поэтому рост корреляции со временем можно объяснить тем, что за последние десятилетия рынки стали более волатильными. Например, с 2000 по 2009 год было 95 торговых сессий, когда S&P 500 сдвинулся на 3% и больше. А за предшествующие 50 лет был всего 81 случай.
Количество дней в каждом десятилетии, когда S&P 500 сдвинулся на 3% и более
| 1950—1959 | 5 |
| 1960—1969 | 9 |
| 1970—1979 | 16 |
| 1980—1989 | 24 |
| 1990—1999 | 27 |
| 2000—2009 | 95 |
| 2010—2019 | 50 |
Особенно явно корреляции усиливаются во время фондовых обвалов. В панике инвесторы массово скидывают ценные бумаги широкого спектра, и в итоге все падает независимо от корреляции.
Поэтому на спокойном рынке с 2014 по 2017 год положительно коррелировали между собой только высокорисковые активы: S&P 500, глобальные акции, бумаги развивающихся рынков и фонды REIT. А низкорисковые активы были связаны только между собой. Это, например, муниципальные, корпоративные облигации, долгосрочные трежерис. При этом корреляции между этими двумя группами активов практически не наблюдалось.
Но во время коронавирусного кризиса корреляции усилились. Все перечисленные выше активы стали взаимосвязаны. А облигации, которые традиционно считаются защитным инструментом, падали вместе с рисковыми активами.
Как посчитать корреляцию
Чтобы рассчитать корреляцию, можно воспользоваться онлайн-калькулятором, например от Portfolio Visualizer или более простым вариантом от Unicornbay.
Я использовал Portfolio Visualizer, чтобы проверить корреляции между такими классами активов:
Для этого я вбил через пробелы указанные тикеры, выбрал расчет корреляций на основе месячной доходности инструментов и рассчитал 36-месячную скользящую.
Корреляции рассчитывались в рамках окна шириной три года, которое двигалось по шкале времени с марта 2006 по февраль 2021 года. Скользящая корреляция за 36 месяцев позволяет увидеть, как менялись ее значения с течением времени.
Я начал расчет с марта 2006 года, так как для фонда DBC более ранних данных нет.
Результаты расчетов представлены в таблице. Мы видим, что исторически у недвижимости, коммодити и S&P 500 слабая отрицательная корреляция по отношению к долгосрочным и коротким облигациям.
36-месячная скользящая корреляция разных классов активов
| Название | Тикер | TLT | SHY | SPY | GLD | DBC | VNQ |
|---|---|---|---|---|---|---|---|
| iShares 20+ Year Treasury Bond ETF | TLT | — | 0,54 | −0,32 | 0,23 | −0,37 | −0,01 |
| iShares 1-3 Year Treasury Bond ETF | SHY | 0,54 | — | −0,37 | 0,29 | −0,21 | −0,18 |
| SPDR S&P 500 ETF Trust | SPY | −0,32 | −0,37 | — | 0,05 | 0,54 | 0,72 |
| SPDR Gold Shares | GLD | 0,23 | 0,29 | 0,05 | — | 0,36 | 0,09 |
| Invesco DB Commodity Tracking | DBC | −0,37 | −0,21 | 0,54 | 0,36 | — | 0,34 |
| Vanguard Real Estate ETF | VNQ | −0,01 | −0,18 | 0,72 | 0,09 | 0,34 | — |
Как рассчитать корреляцию в «Экселе»
Скользящие корреляции также достаточно легко рассчитать в «Экселе». В этом помогает функция КОРРЕЛ() — или CORREL() в англоязычной версии.
Для начала необходимо сформировать два массива данных с котировками интересующих инструментов. Для примера я возьму акции «Газпрома» (GAZP) и Сбербанка (SBER) и выгружу цены бумаг на конец каждого месяца с 1 марта 2015 по 1 марта 2021 года. Всего получилось 73 месяца.
После этого можно воспользоваться функцией КОРРЕЛ(), чтобы посчитать скользящие корреляции. Я приведу пример, как рассчитать скользящую трехмесячную, то есть значение за каждое предыдущее окно в три месяца.
Что в итоге
Корреляция показывает схожесть поведения активов. Понимание корреляций активов используется при диверсификации, а также оптимизации стратегии согласно современной теории портфеля.
Корреляция рассчитывается на конкретном временном отрезке, и она может меняться. Как показывают исторические данные, с течением времени корреляция растет.
Корреляция усиливается на падающих рынках и вместе с увеличением волатильности.
Что делать? Читатели спрашивают — эксперты Т—Ж отвечают
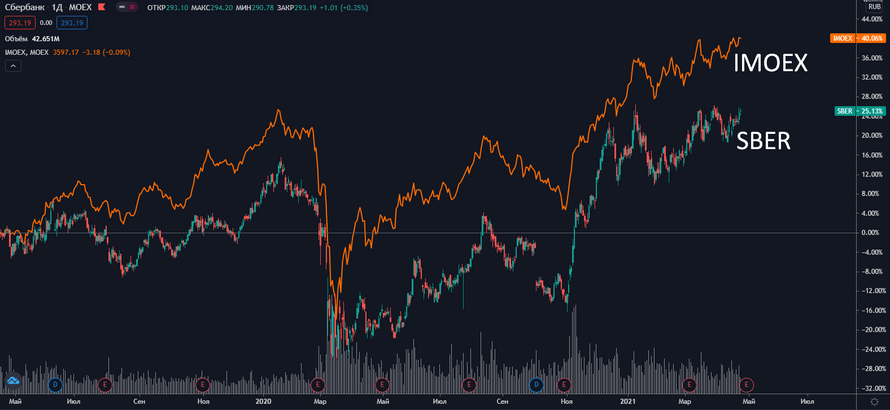
MarketTwits, как-то неправильно приводить в пример корреляцию акции и индекса, состоящего на 1/6 из этих акций. Вот Русгидро и Сбер сравнить да, выбрать их индекса максимально отрицательно коррелирующие и составить свой идеальный индекс)
Значение слова «корреляция»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Математической мерой корреляции двух случайных величин служит корреляционное отношение
либо коэффициент корреляции
). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
КОРРЕЛЯ’ЦИЯ, и, ж. [латин. correlatio] (науч.). 1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.). 2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
корреля́ция
1. матем. статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми) ◆ Высок коэффициент парной корреляции между переменными x₁ и x₃ (коэффициент корреляции 0,9), что показывает их тесную корреляционную взаимосвязь. К. М. Семенович, Б. П. Чупрынов, «Математика для экономистов: Учебное пособие», 2015 г. (цитата из библиотеки Google Книги) ◆ Если, когда увеличивается одно значение, то в большинстве случаев увеличивается и второе, корреляция положительная, а если одно значение уменьшается при увеличении второго, то тут корреляция уже отрицательная, или обратная. Пример отрицательной корреляции — график, показывающий, как соотносится температура воздуха с высотой над уровнем моря. Чем выше на гору вы забираетесь, тем холоднее воздух. М. Эскью, Р. Истуэй, «Математика с удовольствием!», 2017 г. (цитата из библиотеки Google Книги)
2. психол. взаимное соотношение, соответствие понятий и явлений ◆ Всё большее количество фактов поддерживают теорию, согласно которой существует корреляция между Я-концепцией и успеваемостью в школе. У успешных учеников более развитое чувство достоинства, и они в какой-то мере лучше относятся к себе (Garzarelli, Ever art, and Lester, 1993). Тем не менее эта связь обратима. Те, у кого высокая самооценка, лучше учатся в школе, а те, кто хорошо учится в школе, имеют более высокую самооценку… Ф. Райс, «Психология подросткового и юношеского возраста», 2010 г. (цитата из библиотеки Google Книги) ◆ Положительные, но умеренные по величине корреляции между учебными оценками и результатами тестирования не позволяли исследователям однозначно утверждать, что интеллект детерминирует успешность обучения. В. Н. Дружинин, «Психология общих способностей. 3-е изд.», 2013 г. (цитата из библиотеки Google Книги) ◆ «Корреляция» в прямом переводе означает соотношение. Если изменение одной переменной сопровождается изменением другой, то говорят о корреляции этих переменных. Наличие корреляции двух переменных не является свидетельством наличия причинно-следственных зависимостей между ними, но даёт возможность выдвинуть такую гипотезу. Отсутствие корреляции позволяет опровергнуть гипотезу о причинно-следственной связи переменных. М. Коновалова, «Экспериментальная психология: конспект лекций», 2017 г. (цитата из библиотеки Google Книги)
3. книжн. взаимная связь явлений, соотношение ◆ Корреляция между атмосферным давлением и влажностью воздуха. ◆ Количество уголовных преступлений и рост безработицы находятся друг к другу в прямой корреляции.
4. биол. взаимная согласованность функций частей и строения и животного или растения, которая поддерживает постоянство его внутренней среды и является следствием приспособления организма к условиям его существования ◆ Закон корреляции (Ж. Кювье, 1793): в организме, как целостной системе, все его части соответствуют друг другу как по строению, так и по выполняемым функциям. Р. Е. Михайловна, Ш. Т. Матвеевна, Ш. Л. Алексеевна, «Биология (Учебник)», 2016 г. (цитата из библиотеки Google Книги)
5. лог. отношение между двумя одинаковыми по форме связями; в случае, если одна связь становится изоморфной другой, тогда это — корреляция, а само закономерное структурное изменение – коррелятор
Корреляции для начинающих
Апдейт для тех, кто сочтет статью полезной и занесет в избранное. Есть приличный шанс, что пост уйдет в минуса, и я буду вынужден унести его в черновики. Сохраняйте копию!
Краткий и несложный материал для неспециалистов, рассказывающий в наглядной форме о различных методах поиска регрессионных зависимостей. Это все и близко не академично, зато надеюсь что понятно. Прокатит как мини-методичка по обработке данных для студентов естественнонаучных специальностей, которые математику знают плохо, впрочем как и автор. Расчеты в Матлабе, подготовка данных в Экселе — так уж повелось в нашей местности
Введение
Зачем это вообще надо? В науке и около нее очень часто возникает задача предсказания какого-то неизвестного параметра объекта исходя из известных параметров этого объекта (предикторов) и большого набора похожих объектов, так называемой учебной выборки. Пример. Вот мы выбираем на базаре яблоко. Его можно описать такими предикторами: красность, вес, количество червяков. Но как потребителей нас интересует вкус, измеренный в попугаях по пятибалльной шкале. Из жизненного опыта нам известно, что вкус с приличной точностью равен 5*красность+2*вес-7*количество червяков. Вот про поиск такого рода зависимостей мы и побеседуем. Чтобы обучение пошло легче, попробуем предсказать вес девушки исходя из ее 90/60/90 и роста.
Исходные данные
В качестве объекта исследования возьму данные о параметрах фигуры девушек месяца Плейбоя. Источник — www.wired.com/special_multimedia/2009/st_infoporn_1702, слегка облагородил и перевел из дюймов в сантиметры. Вспоминается анекдот про то, что 34 дюйма — это как два семнадцатидюймовых монитора. Также отделил записи с неполной информацией. При работе с реальными объектами их можно использовать, но сейчас они нам только мешают. Зато их можно использовать для проверки адекватности полученных результатов. Все данные у нас непрерывные, то есть грубо говоря типа float. Они приведены к целым числам только чтобы не загромождать экран. Есть способы работы и с дискретными данными — в нашем примере это например может быть цвет кожи или национальность, которые принимают одно из фиксированного набора значений. Это больше имеет отношение к методам классификации и принятия решений, что тянет еще на один мануал. Data.xls В файле два листа. На первом собственно данные, на втором — отсеянные неполные данные и набор для проверки нашей модели.
Обозначения
W — вес реальный
W_p — вес, предсказанный нашей моделью
S — бюст
T — талия
B — бедра
L — рост
E — ошибка модели
Как оценить качество модели?
Задача нашего упражнения — получить некую модель, которая описывает какой-либо объект. Способ получения и принцип работы конкретной модели нас пока не волнует. Это просто функция f(S, T, B, L), которая выдает вес девушки. Как понять, какая функция хорошая и качественная, а какая не очень? Для этого используется так называемая fitness function. Самая классическая и часто используемая — это сумма квадратов разницы предсказанного и реального значения. В нашем случае это будет сумма (W_p — W)^2 для всех точек. Собственно, отсюда и пошло название «метод наименьших квадратов». Критерий не лучший и не единственный, но вполне приемлемый как метод по умолчанию. Его особенность в том, что он чувствителен по отношению к выбросам и тем самым, считает такие модели менее качественными. Есть еще всякие методы наименьших модулей итд, но сейчас нам это пока не надо.
Простая линейная регрессия
Самый простой случай. У нас одна переменная-предиктор и одна зависимая переменная. В нашем случае это может быть например рост и вес. Нам надо построить уравнение W_p = a*L+b, т.е. найти коэффициенты a и b. Если мы проведем этот расчет для каждого образца, то W_p будет максимально совпадать с W для того же образца. То есть у нас для каждой девушки будет такое уравнение:
W_p_i = a*L_i+b
E_i = (W_p-W)^2
Общая ошибка в таком случае составит sum(E_i). В результате, для оптимальных значений a и b sum(E_i) будет минимальным. Как же найти уравнение?
Матлаб
Графичек

Мда, негусто. Это график W_p(W). Формула на графике показывает связь W_p и W. В идеале там будет W_p = W*1 + 0. Вылезла дискретизация исходных данных — облако точек клетчатое. Коэффициент корреляции ни в дугу — данные слабо коррелированы между собой, т.е. наша модель плохо описывает связь веса и роста. По графику это видно как точки, расположенные в форме слабо вытянутого вдоль прямой облака. Хорошая модель даст облако растянутое в узкую полосу, еще более плохая — просто хаотичный набор точек или круглое облако. Модель необходимо дополнить. Про коэффициент корреляции стоит рассказать отдельно, потому что его часто используют абсолютно неправильно.
Расчет в матричном виде
Мультилинейная регрессия
Попытка номер два

А так получше, но все равно не очень. Как видим, клетчатость осталась только по горизонтали. Никуда не денешься, исходные веса были целыми числами в фунтах. То есть после конверсии в килограммы они ложатся на сетку с шагом около 0.5. Итого финальный вид нашей модели:
W_p = 0.2271*S + 0.1851*T + 0.3125*B + 0.3949*L — 72.9132
Объемы в сантиметрах, вес в кг. Поскольку у нас все величины кроме роста в одних единицах измерения и примерно одного порядка по величине (кроме талии), то мы можем оценить их вклады в общий вес. Рассуждения примерно в таком духе: коэффициент при талии самый маленький, равно как и сами величины в сантиметрах. Значит, вклад этого параметра в вес минимален. У бюста и особенно у бедер он больше, т.е. сантиметр на талии дает меньшую прибавку к массе, чем на груди. А больше всего на вес влияет объем задницы. Впрочем, это знает любой интересующийся вопросом мужчина. То есть как минимум, наша модель реальной жизни не противоречит.
Валидация модели
Название громкое, но попробуем получить хотя бы ориентировочные веса тех девушек, для которых есть полный набор размеров, но нет веса. Их 7: с мая по июнь 1956 года, июль 1957, март 1987, август 1988. Находим предсказанные по модели веса: W_p=X*repr 
Что ж, по крайней мере в текстовом виде выглядит правдоподобно. А насколько это соответствует реальности — решать вам
Применимость
Если вкратце — полученная модель годится для объектов, подобных нашему набору данных. То есть по полученным корреляциям не стоит считать параметры фигур женщин с весом 80+, возрастом, сильно отличающимся от среднего по больнице итд. В реальных применениях можно считать, что модель пригодна, если параметры изучаемого объекта не слишком отличаются от средних значений этих же параметров для исходного набора данных. Могут возникнуть (и возникнут) проблемы, если у нас предикторы сильно коррелированы между собой. То есть, например это рост и длина ног. Тогда коэффициенты для соответствующих величин в уравнении регрессии будут определены с малой точностью. В таком случае надо выбросить один из параметров, или воспользоваться методом главных компонент для снижения количества предикторов. Если у нас малая выборка и/или много предикторов, то мы рискуем попасть в переопределенность модели. То есть если мы возьмем 604 параметра для нашей выборки (а в таблице всего 604 девушки), то сможем аналитически получить уравнение с 604+1 слагаемым, которое абсолютно точно опишет то, что мы в него забросили. Но предсказательная сила у него будет весьма невелика. Наконец, далеко не все объекты можно описать мультилинейной зависимостью. Бывают и логарифмические, и степенные, и всякие сложные. Их поиск — это уже совсем другой вопрос.